Section Eight - Projected Coordinate Systems

2.8.1: Projection Methods to Projected Coordinate Systems

Up to this point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , we've been examining projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected methods and not projected coordinate systems. Just like when we learned geographic coordinate systems, there were steps we took to move from the geoid a model of the variation between global mean (average) sea level and local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features , which is used to measure precise elevations on the topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." , to a reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid , to a geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. , to a datum, and finally to a geographic coordinate system. Projection methods stop being just methods and start to be projected coordinate systems after two more steps have been taken: 1. a linear unit of measure is decided, and 2. a coordinate system origin is established. All coordinate systems have a single origin point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , a point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. usually labeled (0, 0), however, some systems, like UTM Universal Transverse Mercator , use a different origin value to prevent negative numbers (discussed in more detail in Section 2.8.4). No matter if the origin is labeled (0, 0) or something else, the action is the same where each of the intersections along the X and Y axis are labeled, counting up or down from the origin values.

Utilizing a variety of origin points, which come from moving around one secant line or splitting the difference between to tangential lines, allows for the distortion to be the least along either the X or Y axis, depending on the aspect [geographic coordinate systems] The direction the developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) faces in relation to the geographic coordinate system. Normal; transverse, oblique[topography] The cardinal direction a slope A numeric value - either in percent or degree - expressing the steepness or the rise/run of the landscape. faces (NSEW) of the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method. This movement, in addition to a large selection of reference ellipsoids allows for the maps we create to have the highest accuracy and precision paired with the least amount of distortion while still using linear units.

As stated above, the second factor that a projected coordinate system needs that takes it from a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method to establish the linear units it's going to use, most commonly, feet, meters, and international feet. When a geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. 's intersections are labeled via measuring from either the equator or principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. , angles are easier to use since we are dealing with a sphere which later goes through a affine transformation to become an ellipsoid. When we are making measurements on a flat map - a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected - we then switch to linear units of measure, which are much more convenient and make more sense to us.

To review, a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method includes selecting a projected coordinate system, a developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) , such as a cone, cylinder, or flat plane (azimuthal), and an aspect [geographic coordinate systems] The direction the developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) faces in relation to the geographic coordinate system. Normal; transverse, oblique[topography] The cardinal direction a slope A numeric value - either in percent or degree - expressing the steepness or the rise/run of the landscape. faces (NSEW) , selecting which direction to turn the Earth within the given developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) . It becomes a projected coordinate system when a linear unit and a single secant line or pair of tangential lines have been selected prior to transferring the land and ocean masses to the developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) , which is then cut and unrolled into a flat map. The selection of the placement of the secant or tangential lines define the location of the system's origin, as these lines will have the least amount of distortion. Selecting and moving the secant or tangential lines is made easier with software like ArcGIS, since it allows you to simple type in which line(s) you'd like to use and it makes all of the adjustments necessary.

As you will learn throughout the semester, there are several words in GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences which are used incorrectly or may have a double meaning. This is in no way done to confuse you (really), but it’s just a language that has been used by lots of folks, most of whom came from other sciences. As GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences is a fairly young science, most of it, including the terminology, comes from other places. This, in addition to a whole lot of "DIY GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences ", has led to a fair number of words which are used either incorrectly, partially correct, or that have two, and sometimes three, meanings. The term " projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected " is one of those words which, in addition to having a couple of meanings (which, luckily, are mostly correct and mostly similar), is used as a rather "all encompassing" term to mean "geographic coordinate system", "projected coordinate system", " projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method", and "convert data from one coordinate system to another".

Technically, the word " projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected " or "to project" is in reference to the action of creating a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected and "projected coordinate system (PCS)" is the result of the action, after a linear unit and system origin has been set. For example, "Lambert Conformal Conic" is However, you’ll almost always here a projected coordinate system (and geographic coordinate systems, for that fact) referred to as a " projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected ", simply because it’s shorter and easier. This text attempts to use the correct terms in the correct places while you’re still learning the process, but later will switch to using " projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected " to mean both the action and the product - but by then, you’ll be able to note the difference in context.

We noted earlier that the word projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected refers to the method used to create a the first part of a projected coordinate system. This idea will come up again when we begin to explore coordinate systems (both geographic and projected) in the GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences software. For every projected coordinate system, it will have a very specific name that represents where is should be used and the method by which it was created, as well as additional information about the method with which it was created - including the name. That is to say, the name of the PCS is the most specific thing, consisting of where you should use that particular PCS and the method it was created, and not exactly to be redundant, as there are always cases which vary from the norm, you will find the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method listed, which is slightly less specific. For example, you might see USA Contiguous Lambert Conformal Conic as the specific name of a projected coordinate system and Lambert Conformal Conic as the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method. The name Lambert Conformal Conic, as we learned earlier, means the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected method used a cone as the developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) and it is meant to be used with projected coordinate systems which need to preserve shape ( conformal serve the purpose of preserving shape, distance, and bearing, at the expense of area and scale ) within the contiguous United States.

2.8.2: Map Scale

Before we look at how to choose a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , lets first look at the idea of map scale a mathematical representation expressing distance on a map vs distance on the ground . Map scale is simply the mathematical ratio of the distance between two points represented on a map and the same two points in the real world expressed in one of two ways:

A Statement of EquivalencyorVerbal Scale
A Representative Fraction
Scale Bars

Statement of Equivalency or Verbal Scale

A statement of equivalency (also known as ''verbal scale''): the relative scale is expressly defined on a map: 1 cm = 1 kilometer; 1 inch = 10 miles (also known asverbal scale) is when the relative scale is expressly defined on a map: 1cm = 1 kilometer; 1 inch = 10 miles, 5 nanometers = 12 kilometers (even though that last one would be a bit silly to use). For every measured unit on the map, one would travel the same distance in the real world. For the map where one inch equals ten miles, if you were to use a wooden ruler and measure an inch on the map, you can safely assume that the distance between those two points in the real world would be 10 miles.

The catch with a statement of equivalency (also known as ''verbal scale''): the relative scale is expressly defined on a map: 1 cm = 1 kilometer; 1 inch = 10 miles is, however, that the statement is only good for those units. If you were to measure the same map as above in centimeters, you could not assume that the distance between one centimeter is going to be ten miles. You could, using unit conversion, assume that 2.54 centimeters on the map would equal ten miles, however, but that means you'd be doing a whole lot of math and conversions. This is why, when you don't know what units your map's audience best thinks in, is to use representative fractions instead.

Representative Fractions

Similar to statements of equivalency, a representative fraction expression of map scale in ratio form utilizing non-specific linear unit, such as 1 map unit equals 250,000 real world units, or 1:250,000 is unitless. Presented as a ratio such as1:24,000; 1:100,000; 1:1,000,000; and so on, one unit on the map equals the stated units in the real world. In other words, a map that has a scale of 1:24,000 means that one inch equals 24,000 inches in the real world OR 1 centimeter equals 24,000 centimeters in the real world. With representative fractions, you don't need to assume what units your audience thinks best in, but you also assume they know how many inches are in a mile, since the representative fractions only work with a single unit at a time.

Scale Bars

Lastly, with maps, we often see scale bars drawn on the bottom. Like a statement of equivalency (also known as ''verbal scale''): the relative scale is expressly defined on a map: 1 cm = 1 kilometer; 1 inch = 10 miles , the scale bar will be shown in a set unit of measure, and not a representative fraction expression of map scale in ratio form utilizing non-specific linear unit, such as 1 map unit equals 250,000 real world units, or 1:250,000 . Unlike statement of equivalencies, however, you could potentially use a ruler of a different unit scale to measure the map. If the map scale a mathematical representation expressing distance on a map vs distance on the ground bar is shown in inches and miles, you could use a centimeter ruler to find the distancein miles. You're not exactly limited by the unit of measure of the ruler, but since the scale bar is set up for one kind of units, you can't convert the units back and forth, but you could successfully use a different kind of ruler.

One note: When it comes to reproducing maps, the only one of these three which stays constant is a scale bar. Statement of equivalencies and representative fractions are only true for the size of map the originally refereed to. If a map is copied at a smaller or larger size, the two ratios will be incorrect while the scale bar remains correct.

Large and Small Scale

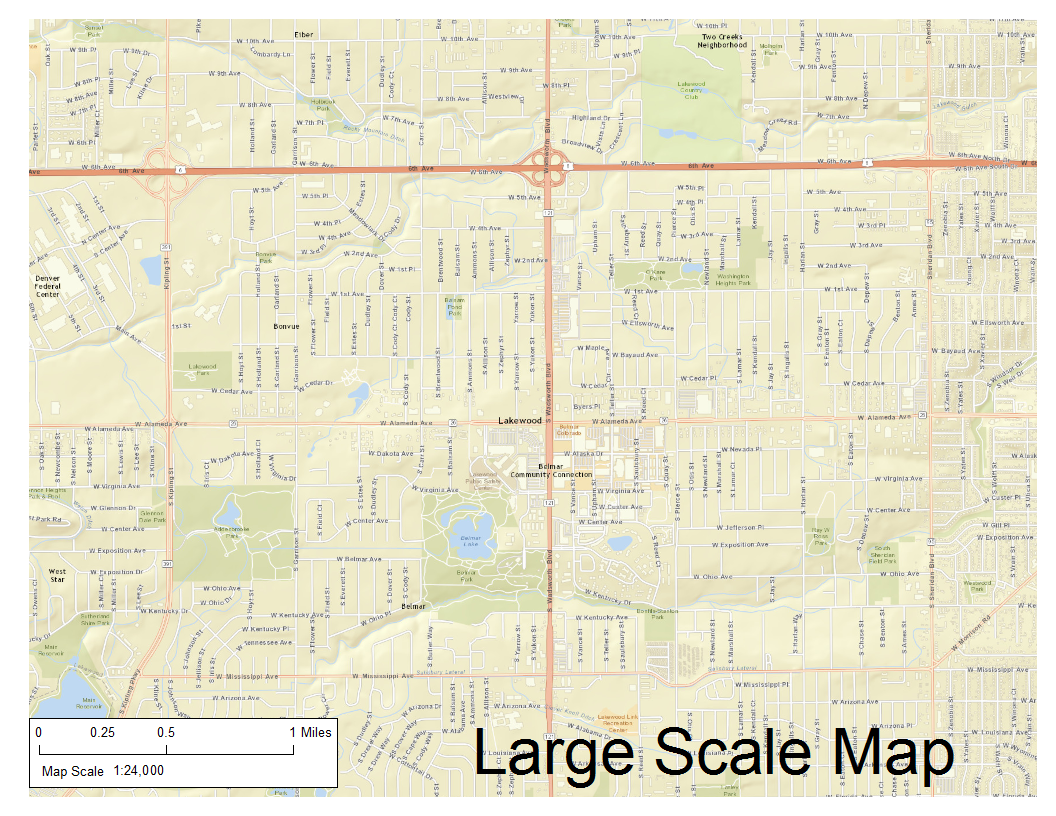
In GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences and cartography, we often use the terms small scale, which are equally as often mixed up. When we look at the representative fraction expression of map scale in ratio form utilizing non-specific linear unit, such as 1 map unit equals 250,000 real world units, or 1:250,000 scale of a map and see a large number in the denominator, we tend toincorrectlyconclude the map is the large scale, when in fact a large denominator leads to a small number (a number a long distance from one on the number line)- thus a small scale map a map where the representative fraction is far from one and the objects in the map are relatively small (zoomed out) . Large scale maps have a small denominator where the number is closer to one on the number line.

The confusion is clear. When you see a map with a representative scale fraction with a large denominator and a larger geographic extent, your first inclination is to assume the map has a large scale. If we keep looking back on the representative fraction expression of map scale in ratio form utilizing non-specific linear unit, such as 1 map unit equals 250,000 real world units, or 1:250,000 , we see that fractions with a smaller denominator are closer to one on the number line (and a scale of 1:1 is the real world) and fractions with larger denominators are further away from the representative size being the same as the real world. To keep it straight, think that smaller denominators lead to larger features (more like the real world) and larger features lead to large scale maps.

Figure 2.36: Small and Large Scale Maps

2.8.3: Projection Selection

So far in this Chapter, we have looked at the idea of geodesy the science of measuring and monitoring the size and shape of the Earth and the location of points on its surface and measuring the Earth, representing the Earth’s odd shape as a geoid a model of the variation between global mean (average) sea level and local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features , which is used to measure precise elevations on the topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." and a mathematical ellipsoid, creating measurable locations on the Earth’s surface by combining reference ellipsoids and datums to create geographic coordinate systems, how to use the idea of projections to convert a round Earth to a flat map, and lastly, how different projections are designed to minimize different distortions. Whew! That’s a lot of information - but we are not done quite yet. A solid understanding of how GCS’s and projections are created is essential to understanding how we use them in GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences , so we are going to finish off this chapter with a bit of practical projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected use.

One of the most common questions asked by introduction to GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences students after learning about projections is: "What projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is best for my project"? This is one of those questions which has the unfortunate answer of "Well, that depends". When you look at how projections are created and what distortions come into play with their use, you will start to realize that being able to select the "proper" projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is just an understanding of the gains and setbacks of each kind of projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected . While there are no real “rules” on projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected selection, there are a few guidelines to help you choose:

What distortion can you give up in favor of the one(s) you really need?
- All projected coordinate systems come with some distortion, as we've learned there are no projections which preserve all kinds at one time. The biggest decision of which projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected to use for a project is that of distortion. If you have a project which deals with solving the the area which has changed, selecting a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected which preserves shape will produce errors in the solved measurements. On the other hand, when you go to present your work at the end of the project, keeping the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected which preserved area and distorted shape will look quite odd to your reader.
How big is your project area?
- Now that we understand what scale is in regards to GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences and cartography, we can explore projections in these same terms. As we learned with reference ellipsoids, better accuracy and precision come with better localization, and the same is held true with projections. Selecting a localized projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected will decrease distortion close to the tangential point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , and that distortion will increase as you move away, so choosing a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected designed for use in Florida and applying it to Oregon is most likely a bad idea. And when you are completing a project which covers the entire United States, choosing a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected designed for either Oregon or Florida (or the whole Earth, for that fact) is also a bad idea.
What unit of measure (feet, inches, degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° ...) would you like your map to be measured in?
- We know that geographic coordinate systems consist of a datum, a reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid , and an angular unit of measure the selected units for measuring angles. Choices include degree and radians. (such as degree with the latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° /longitude system) - which means that spatial objects collected in a GCS will be measured in that unit of measure. For example, if you create a GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences layer of roads, and the chosen GCS is WGS84, the length of the roads will be measured in degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° . When we go through the process of creating a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , moving from the round (measured in angles) to the flat, we can move from an angular unit of measure the selected units for measuring angles. Choices include degree and radians. to a linear one, such as feet and meters. When you move the roads layer you created in WGS84, and move it, or project it, from the GCS WGS84 to a flat map (say WGS84 California (Teale) Albers), you are now capable of measuring in feet, yards, and miles.
What is the end goal of your project?
- While we will spend quite a bit of time discussing this in Chapter Nine, for now, we can just look at the end goal as how is it the map should look? Will it be displayed on a wall and you need to preserve shape and size or used for navigation where distance and bearing are important. Choosing the correct projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected leads to the proper end product.

2.8.4: Examples Of Projected Coordinate Systems

In the next section, will look at four common projected coordinate systems and examine how they were made, which - as stated above - will let us in on the benefits of selecting that projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected for a specific project.

Normal Mercator and Transverse Mercator

Normal Mercator

The Normal Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is one of the most common, and most controversial, projections out there. Just like it was stated in the West Wing clip we watched, the Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is a conformal serve the purpose of preserving shape, distance, and bearing, at the expense of area and scale cylindrical projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , tangent at the Equator, and designed to preserve shape, distance, and bearing. Adjacent to the tangential line, distortion is minimal, but increases rapidly as one moves north or south. The Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected (and it’s cousin, Web Mercator) is used for large areas (small scale) nearest the mid-latitudes.

Transverse Mercator

The Transverse Mercator projections, like we learned in the previous section, turn the tangential line from a parallel to a meridian, which reduces distortion along a North-South line, with that distortion increasing moving east or west.

Figure 2.37: Normal and Transverse Mercator Projected Coordinate Systems

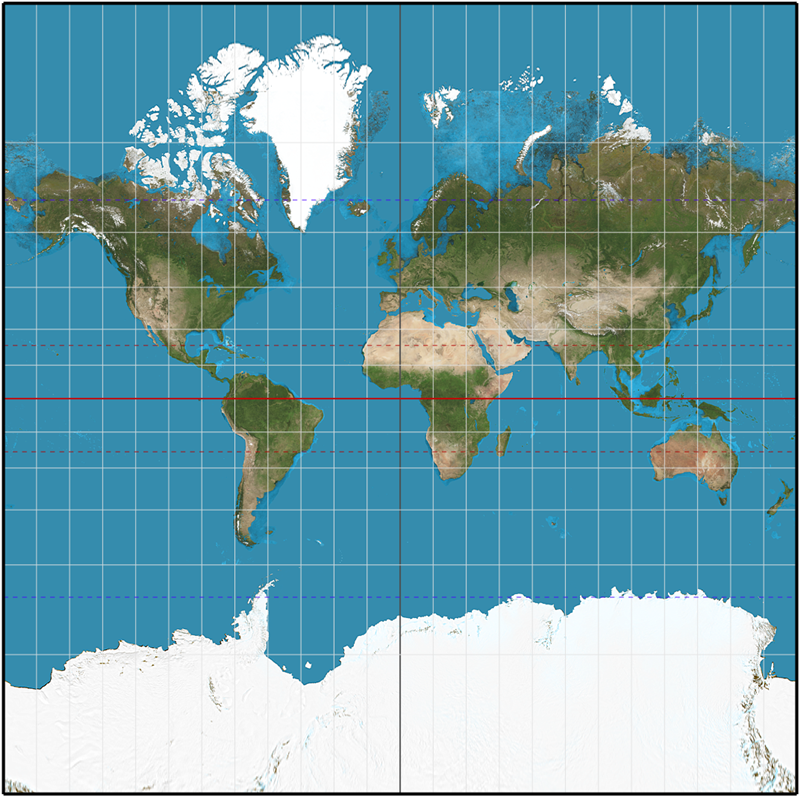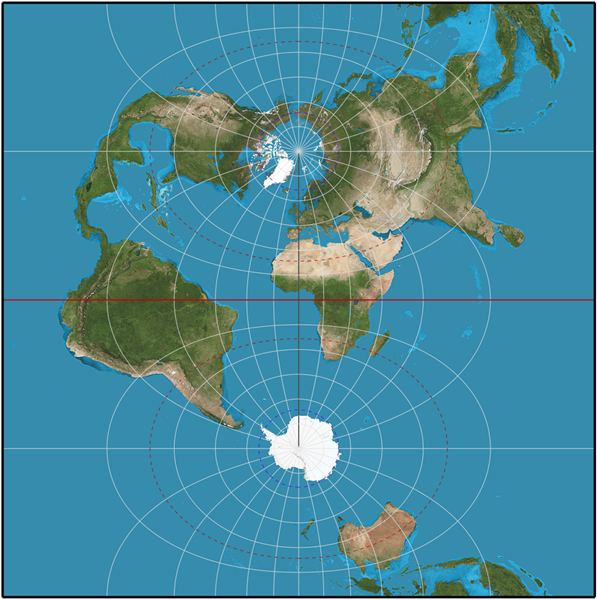Normal Mercator Projected Coordinate System	Transverse Mercator Projected Coordinate System

Lambert Conformal Conic

Looking at the name, we immediately know this projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is designed to preserve shape, distance, and bearing ( conformal serve the purpose of preserving shape, distance, and bearing, at the expense of area and scale ) and is created from a conic developable surface a geometric shape which will not be distorted when flattened. Used as the base shape to transfer features during projections. Most often a cone, cylinder, or plane (azimuthal) (and was designed by a guy named Lambert). Designed by Johann Heinrich Lambert in 1772, the Lambert Conformal Conic projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is used to map large areas (small scale), especially in the mid-latitudes, where the secant lines are placed at roughly 20°N and 60°S.

Figure 2.38: Lambert Conformal Conic Projected Coordinate System

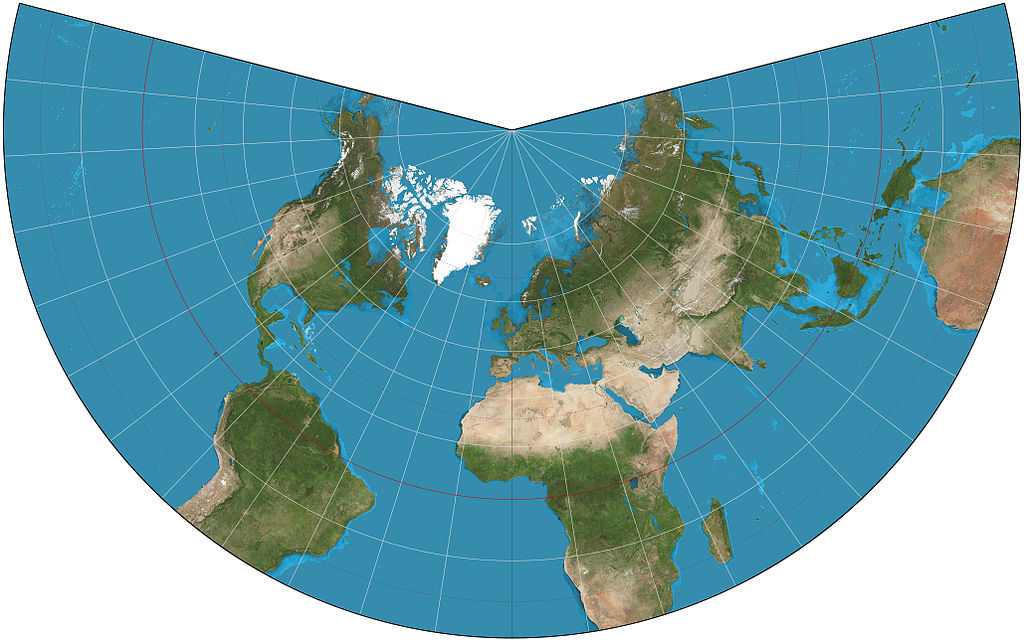Universal Transverse Mercator( UTM Universal Transverse Mercator )

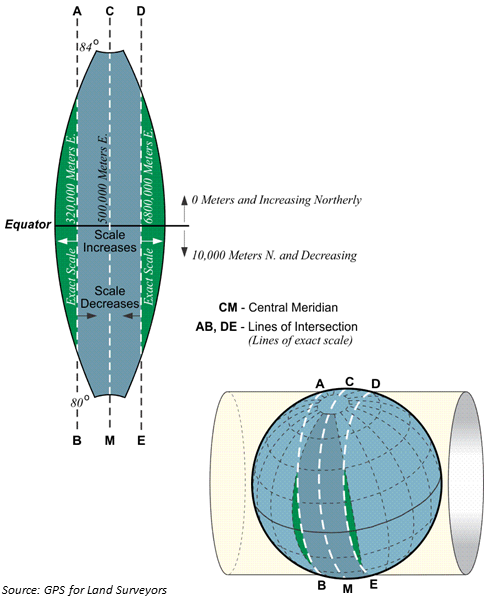
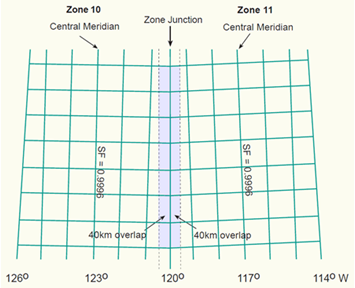
Universal Transverse Mercator is a technically a planar coordinate system the result of converting an angular unit of measure used to locate objects on a geographic coordinate system to a linear unit of measure via a Cartesian Coordinate System. Planar Coordinate Systems utilize linear units such as feet, meters, and international feet. - a specially designed method for finding a location on a two-dimensional map, which is based on a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected . Like with the Lambert Conformal Conic projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , we can look to the name - Universal Transverse Mercator - to see the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is based on the transverse Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected . The “universal” part comes in by altering the transverse methods slightly instead of being tangent at one line and projecting the entire globe, a smaller projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is made by placing the cylinder secant at two lines 6° apart, creating a strip or “zone”. The secant lines are then rotated, and another strip is taken (360° / 6° = 60 zones). By stitching together all 60 zones together, a complete world projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is made with distortion reduced in every zone (vs at a only single meridian). Like the Transverse Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , however, the distortion is too extreme at the poles (the sweet spots are between 84°N and 80°S) and UTM Universal Transverse Mercator is not used.

Figure 2.39: Universal Transverse Mercator Projected Coordinate System

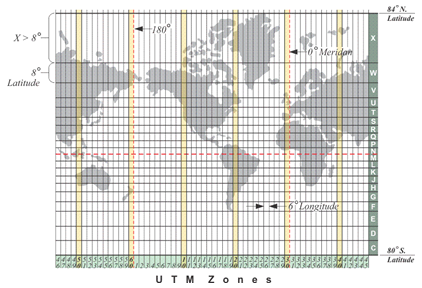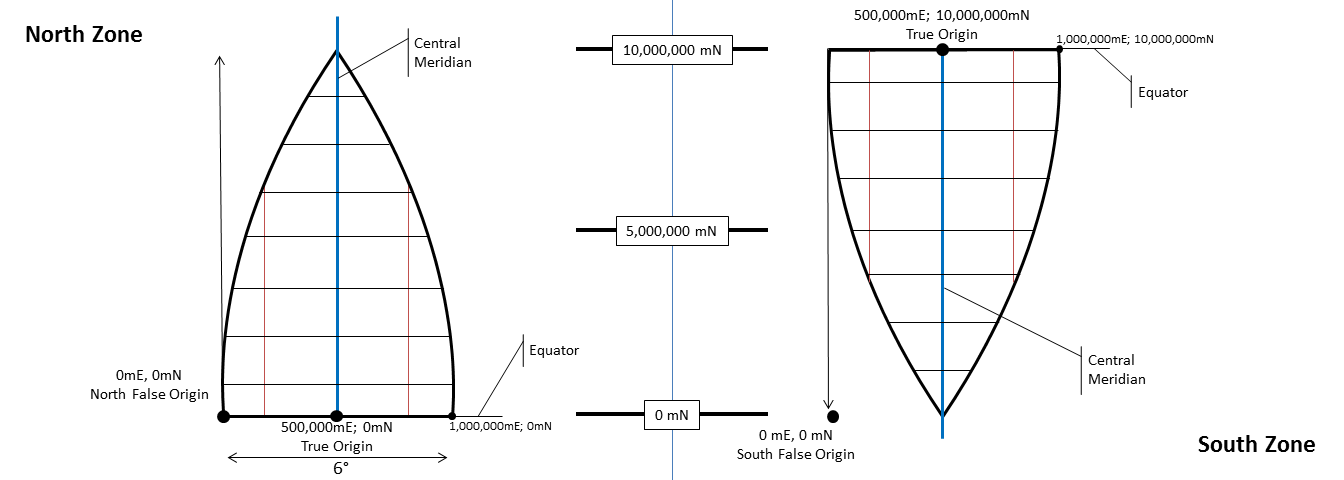
Since UTM Universal Transverse Mercator is a planar coordinate system the result of converting an angular unit of measure used to locate objects on a geographic coordinate system to a linear unit of measure via a Cartesian Coordinate System. Planar Coordinate Systems utilize linear units such as feet, meters, and international feet. , it utilizes a Cartesian Coordinate system affixed to an origin and labels XY intersections by measuring the linear distance from that origin. Yet, the UTM Universal Transverse Mercator system delivers the geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. in a unique way - with 60 different origins, one for each zone.

Using the equator as the X axis, each UTM Universal Transverse Mercator zone is bisected right down the middle creating a central meridian, with 3° on the east and 3° on the west (and the Y axis). North of the equator is the North Zone, denoted with the number of the zone and an N, such as Zone 18N, and an S for south, such as Zone 18S. If the origin was labeled 0,0 where the equator and central meridian intersect in each zone, that means there would have to be negative numbers - those west of the central meridian and south of the equator. To combat the negative numbers, the 0,0 was arbitrarily changed to 500,000 and 10,000,000, meaning coordinates west of the central meridian start counting down from 499,999 meters and south of the equator count down from 9,999,999 meters. Since UTM Universal Transverse Mercator measurements come from a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected and not a GCS, the terms false easting and false northing are used in place of North and East, like we see with Latitude and Longitude.

Whew! That was a lot of information in two paragraphs. Let’s look at some examples to help understand what we just read.

Figure 2.40: The UTM Universal Transverse Mercator System Explained

First, we place the cylinder secant along two lines 6° apart to make a zone.	Since our goal is to reduce distortion and create a flat map with planar coordinates, the two curved sections are overlapped with the neighboring zone to make a rectangular strip.

The North and South halves of each zone contains a false and a true origin, with the false origin located at 0 mE, 0mN, as expected, and the false origin located where the central meridian and equator intersect. The North Zone true origin is located at 5000,000 mE, 0mN while the South Zone true origin is located at 500,000 mE, 10,000,000mN. The arbitrary numbers assigned to the false origins prevents the use of negative numbers for UTM Universal Transverse Mercator coordinates. Since each zone is labeled the same way in reference to the UTM Universal Transverse Mercator coordinates, each unique coordinate pair occurs 120 times, thus making the addition of the zone number and North or South designation imperative for the coordinate label. For example, 420235 mE, 3868323mN occurs 120 times, but UTM Universal Transverse Mercator 11N 420235 mE, 3868323mN occurs only once.

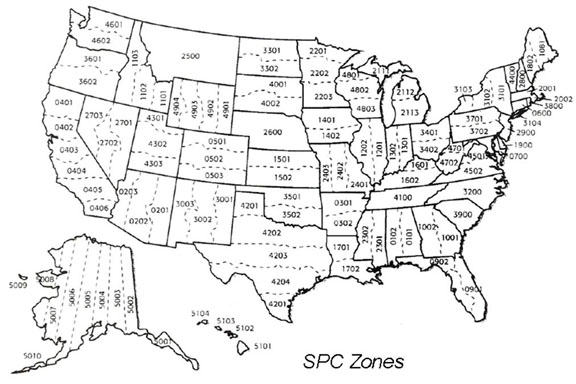
State Plane Coordinate System(SPCS)

The UTM Universal Transverse Mercator planar coordinate system the result of converting an angular unit of measure used to locate objects on a geographic coordinate system to a linear unit of measure via a Cartesian Coordinate System. Planar Coordinate Systems utilize linear units such as feet, meters, and international feet. is a great example of a “global” system designed to minimize distortion and locate positions over a large area using series of multiple, smaller projections stitched together. An excellent example of a “local” coordinate system with the same purpose is the State Plane Coordinate System or SPCS.

SPCS breaks the United States into sections by state, and in many cases, breaks states into zones, all with the goal of reducing distortion and labeling locations. For east-west trending states, such as Tennessee and Colorado, utilize a Lambert Conformal Conic projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , while north-south trending states such as Illinois and Mississippi, use a Transverse Mercator projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected (The panhandle of Alaska didn’t fall into either category, thus an Oblique Mercator was used). Thinking about what we’ve learned so far, why were the Lambert Conformal Conic and Transverse Mercator projections used?

Figure 2.41: State Plane Coordinate System (SPCS)

The State Plane Coordinate System (SPCS) with zone numbers

In addition to each state being projected independently to reduce distortion, most of the states were actually broken down further, such as Colorado which contains three zones - Colorado North (0501), Colorado Central (0502), and Colorado South (0503). This means the distortion for each section is about as small as it can be. One thing to note is while distortion is reduced greatly for each zone, the inter-zone distortion can be greater then desired, especially when two neighboring states are created from two base projections.

Like UTM Universal Transverse Mercator , SPCS is a not a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , but rather a planar coordinate system the result of converting an angular unit of measure used to locate objects on a geographic coordinate system to a linear unit of measure via a Cartesian Coordinate System. Planar Coordinate Systems utilize linear units such as feet, meters, and international feet. , utilizing a false origin originally located in Meades Ranch, Kansas (when the system was based on the North American Datum 1927 NAD27), and the idea of counting coordinates with a false easting and a false northing. With an effort to convert angular units of measure ( degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° ) into a Cartesian Coordinate System for ease of navigation, the SPCS was developed in 1930. Since then, the system has been revised a few times, most notably in 1983 after NAD83 was completed, and more recently, when the origin was moved to the center of the Earth to improve calculations when using the system with GPS units. SPCS can be found in feet, meters, and international feet.

Also like UTM Universal Transverse Mercator , the idea of using a technique of projecting small sections and merging them together into a large network can be tough for a new GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences student, since the answer “What projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is your data in?” regarding data near Denver would be “SPCS Colorado Central (0502)”. SPCS is often used as a local projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected (since each zone is based on a projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected ), even though it is technically a planar coordinate system the result of converting an angular unit of measure used to locate objects on a geographic coordinate system to a linear unit of measure via a Cartesian Coordinate System. Planar Coordinate Systems utilize linear units such as feet, meters, and international feet. . Think about it this way: if you are working in Oregon and would like the data to be as exact as possible, you know that if you use Oregon North, the cone used in the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected was tangent to a line running through the center of the zone, vs a cone which was tangent thought the center of the United States for a continent-based projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected . When the projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected is designed for a smaller area, distortion is reduced, larger projections have the least amount of distortion along the tangential line, and increasing distortion from there. If your entire area is only a few hundred miles across, the distortion is negligible, and when the area is thousands of miles across, the distortion is noticeable.

Supported Projected Coordinate Systems

Open in a Separate Page

Projected Coordinate Systems Part One

Name	WKID	Area of Use	Minimum Latitude	Minimum Longitude	Maximum Latitude	Maximum Longitude
Abidjan_1987_TM_5_NW	2165	Cote d'Ivoire (Ivory Coast) - offshore	1.02	-7.55	5.19	-3.11
Abidjan_1987_UTM_Zone_29N	2043	Cote d'Ivoire (Ivory Coast) - west of 6°W	4.29	-8.61	10.74	-6
Abidjan_1987_UTM_Zone_30N	2041	Cote d'Ivoire (Ivory Coast) - east of 6°W	4.92	-6	10.46	-2.48
AbInvA96_2020_Grid	9387	UK - Aberdeen to Inverness	57.1	-4.3	57.7	-2.1
Accra_Ghana_Grid	2136	Ghana - onshore	4.67	-3.25	11.16	1.23
Accra_TM_1_NW	2137	Ghana - offshore	1.4	-3.79	6.06	2.1
Adindan_UTM_Zone_35N	20135	Africa - South Sudan and Sudan - 24°E to 30°E	4.21	23.99	22.01	30.01
Adindan_UTM_Zone_36N	20136	Africa - Ethiopia and Sudan - 30°E to 36°E	3.49	29.99	22.24	36
Adindan_UTM_Zone_37N	20137	Africa - Eritrea, Ethiopia and Sudan - 36°E to 42°E	3.4	36	22.01	42
Adindan_UTM_Zone_38N	20138	Ethiopia - east of 42°E	4.11	42	12.85	47.99
Afgooye_UTM_Zone_38N	20538	Somalia - 42°E to 48°E, N hemisphere onshore	0	42	11.52	48
Afgooye_UTM_Zone_39N	20539	Somalia - onshore east of 48°E	4.44	48	12.03	51.47
Africa_Albers_Equal_Area_Conic	102022	Africa	-35	-25	39	55
Africa_Equidistant_Conic	102023	Africa	-35	-25	39	55
Africa_Lambert_Conformal_Conic	102024	Africa	-35	-25	39	55
Africa_Sinusoidal	102011	Africa	-35	-25	39	55
AGD_1966_ACT_Grid_AGC_Zone	102071	Australia - Australian Capital Territory	-35.93	148.76	-35.12	149.4
AGD_1966_ACT_Standard_Grid	5825	Australia - Australian Capital Territory	-35.93	148.76	-35.12	149.4
AGD_1966_AMG_Zone_48	20248	Australia - 102°E to 108°E	-56	102	-10	108
AGD_1966_AMG_Zone_49	20249	Australia - 108°E to 114°E (EEZ)	-37.84	109.23	-17.19	114
AGD_1966_AMG_Zone_50	20250	Australia - 114°E to 120°E (EEZ)	-38.53	114	-12.61	120
AGD_1966_AMG_Zone_51	20251	Australia - 120°E to 126°E	-38.07	120	-10.46	126.01
AGD_1966_AMG_Zone_52	20252	Australia - 126°E to 132°E	-37.38	125.99	-9.1	132
AGD_1966_AMG_Zone_53	20253	Australia - 132°E to 138°E	-40.71	132	-8.88	138.01
AGD_1966_AMG_Zone_54	20254	Australasia - Australia and PNG - 138°E to 144°E	-46.63	138	-2.53	144.01
AGD_1966_AMG_Zone_55	20255	Australasia - Australia and PNG - 144°E to 150°E	-47.2	144	-1.3	150.01
AGD_1966_AMG_Zone_56	20256	Australasia - Australia and PNG - 150°E to 156°E	-46.44	150	-2.32	156
AGD_1966_AMG_Zone_57	20257	Australia - 156°E to 162°E	-35.13	156	-14.08	162.01
AGD_1966_AMG_Zone_58	20258	Australia - EEZ east of 162°E	-34.22	162	-27.25	163.2
AGD_1966_ISG_54_2	102072	Australia - New South Wales - 140~E to 142~E (ISG 54/2)	-46.63	140	-28.15	142
AGD_1966_ISG_54_3	102073	Australia - New South Wales - 142~E to 144~E (ISG 54/3)	-46.63	142	-28.15	144
AGD_1966_ISG_55_1	102074	Australia - New South Wales - 144~E to 146~E (ISG 55/1)	-47.2	144	-28.15	146
AGD_1966_ISG_55_2	102075	Australia - New South Wales - 146~E to 148~E (ISG 55/2)	-47.2	146	-28.15	148
AGD_1966_ISG_55_3	102076	Australia - New South Wales - 148~E to 150~E (ISG 55/3)	-47.2	148	-28.15	150
AGD_1966_ISG_56_1	102077	Australia - New South Wales - 150~E to 152~E (ISG 56/1)	-46.44	150	-28.15	152
AGD_1966_ISG_56_2	102078	Australia - New South Wales - 152~E to 154~E (ISG 56/2)	-46.44	152	-28.15	154
AGD_1966_ISG_56_3	102079	Australia - New South Wales - 154~E to 156~E (ISG 56/3)	-46.44	154	-28.15	156
AGD_1966_ISG_57_2	102961	Australia - Lord Howe Island - 158~E to 160~E (ISG 57/2)	-47.2	158	-28.15	160
AGD_1966_VICGRID	3110	Australia - Victoria	-39.2	140.96	-33.98	150.04
AGD_1984_AMG_Zone_48	20348	Australia - 102°E to 108°E	-56	102	-10	108
AGD_1984_AMG_Zone_49	20349	Australia - 108°E to 114°E (EEZ)	-37.84	109.23	-17.19	114
AGD_1984_AMG_Zone_50	20350	Australia - 114°E to 120°E (EEZ)	-38.53	114	-12.61	120
AGD_1984_AMG_Zone_51	20351	Australia - 120°E to 126°E	-38.07	120	-10.46	126.01
AGD_1984_AMG_Zone_52	20352	Australia - SA and WA 126°E to 132°E	-37.05	125.99	-9.37	132.01
AGD_1984_AMG_Zone_53	20353	Australia - SA 132°E to 138°E	-36.14	132	-25.99	138
AGD_1984_AMG_Zone_54	20354	Australia - SA and Qld 138°E to 144°E	-38.13	138	-9.86	144.01
AGD_1984_AMG_Zone_55	20355	Australia - Qld 144°E to 150°E	-29.01	144	-14.01	150
AGD_1984_AMG_Zone_56	20356	Australia - Qld east of 150°E	-29.19	150	-22	153.61
AGD_1984_AMG_Zone_57	20357	Australia - 156°E to 162°E	-35.13	156	-14.08	162.01
AGD_1984_AMG_Zone_58	20358	Australia - EEZ east of 162°E	-34.22	162	-27.25	163.2
Ain_el_Abd_1970_Aramco_Lambert_2	102204	Saudi Arabia - onshore	16.37	34.51	32.16	55.67
Ain_el_Abd_Aramco_Lambert	2318	Saudi Arabia - onshore	16.37	34.51	32.16	55.67
Ain_el_Abd_UTM_Zone_36N	20436	Saudi Arabia - onshore west of 36°E	26.82	34.51	29.38	36
Ain_el_Abd_UTM_Zone_37N	20437	Saudi Arabia - onshore 36°E to 42°E	16.59	36	32.16	42
Ain_el_Abd_UTM_Zone_38N	20438	Asia - Middle East - Kuwait and Saudi - 42°E to 48°E	16.37	42	31.15	48.01
Ain_el_Abd_UTM_Zone_39N	20439	Asia - Middle East - Kuwait and Saudi - 48°E to 54°E	17.94	47.99	30.04	54.01
Ain_el_Abd_UTM_Zone_40N	20440	Saudi Arabia - east of 54°E	19.66	54	22.77	55.67
Albanian_1987_GK_Zone_4	2462	Albania - onshore	39.64	19.22	42.67	21.06
American_Samoa_1962_StatePlane_ American_Samoa_FIPS_5300	65062	American Samoa	-17.56	-173.75	-10.02	-165.2
American_Samoa_1962_UTM_Zone_2S	102116	American Samoa	-17.56	-173.75	-10.02	-165.2
Anguilla_1957_British_West_Indies_Grid	2000	Anguilla - onshore	18.11	-63.22	18.33	-62.92
Antigua_1943_British_West_Indies_Grid	2001	Antigua - onshore	16.94	-61.95	17.22	-61.61
Aratu_UTM_Zone_22S	20822	Brazil - 54°W to 48°W and Aratu	-35.71	-53.38	-25.01	-47.99
Aratu_UTM_Zone_23S	20823	Brazil - 48°W to 42°W and Aratu	-33.5	-48.01	0	-41.99
Aratu_UTM_Zone_24S	20824	Brazil - 42°W to 36°W and Aratu	-26.35	-42.01	0.01	-36
Aratu_UTM_Zone_25S	5337	Brazil - 36°W to 30°W offshore	-20.11	-36	0	-30
Arc_1950_UTM_Zone_34S	20934	Africa - Botswana and Zambia - west of 24°E	-26.88	19.99	-10.86	24
Arc_1950_UTM_Zone_35S	20935	Africa - Botswana, Zambia and Zimbabwe - 24°E to 30°E	-25.84	24	-8.31	30
Arc_1950_UTM_Zone_36S	20936	Africa - Malawi, Zambia and Zimbabwe - east of 30°E	-22.42	30	-8.19	35.93
Arc_1960_UTM_Zone_35N	21095	Uganda - north of equator and west of 30°E	0	29.71	0.86	30
Arc_1960_UTM_Zone_35S	21035	Africa - Tanzania and Uganda - south of equator and west of 30°E	-6.81	29.34	0	30
Arc_1960_UTM_Zone_36N	21096	Africa - Kenya and Uganda - north of equator and 30°E to 36°E	0	29.99	4.63	36
Arc_1960_UTM_Zone_36S	21036	Africa - Kenya, Tanzania and Uganda - south of equator and 30°E to 36°E	-11.61	29.99	0.01	36
Arc_1960_UTM_Zone_37N	21097	Kenya - north of equator and east of 36°E	0	36	4.49	41.91
Arc_1960_UTM_Zone_37S	21037	Africa - Kenya and Tanzania - south of equator and east of 36°E	-11.75	36	0	41.6
Argentina_Zone_1	22191	Argentina - west of 70.5°W	-52	-73.59	-36.16	-70.5
Argentina_Zone_2	22192	Argentina - 70.5°W to 67.5°W onshore	-54.9	-70.5	-24.08	-67.49
Argentina_Zone_3	22193	Argentina - 67.5°W to 64.5°W onshore	-55.11	-67.5	-21.78	-64.49
Argentina_Zone_4	22194	Argentina - 64.5°W to 61.5°W onshore	-54.91	-64.5	-21.99	-61.5
Argentina_Zone_5	22195	Argentina - 61.5°W to 58.5°W onshore	-39.06	-61.51	-23.37	-58.5
Argentina_Zone_6	22196	Argentina - 58.5°W to 55.5°W onshore	-38.59	-58.5	-24.84	-55.49
Argentina_Zone_7	22197	Argentina - east of 55.5°W onshore	-28.11	-55.5	-25.49	-53.65
Asia_Lambert_Conformal_Conic	102012	Asia	-10	25	85	185
Asia_North_Albers_Equal_Area_Conic	102025	Asia - North	10	25	85	185
Asia_North_Equidistant_Conic	102026	Asia - North	10	25	85	185
Asia_North_Lambert_Conformal_Conic	102027	Asia - North	10	25	85	185
Asia_South_Albers_Equal_Area_Conic	102028	Asia - South	-10	25	30	165
Asia_South_Equidistant_Conic	102029	Asia - South	-10	25	30	165
Asia_South_Lambert_Conformal_Conic	102030	Asia - South	-10	25	30	165
Astro_DOS_71_4_SHLG71	7877	St Helena - St Helena Island	-16.08	-5.85	-15.85	-5.58
Astro_DOS_71_4_UTM_zone_30S	7878	St Helena - St Helena Island	-16.08	-5.85	-15.85	-5.58
ATS_1977_MTM_4_Nova_Scotia	2294	Canada - Nova Scotia - east of 63°W	44.64	-63	47.08	-59.73
ATS_1977_MTM_5_Nova_Scotia	2295	Canada - Nova Scotia - west of 63°W	43.41	-66.28	46.02	-63
ATS_1977_New_Brunswick_ Stereographic	2200	Canada - New Brunswick	44.56	-69.05	48.07	-63.7
ATS_1977_UTM_Zone_19N	2219	Canada - Maritime Provinces - west of 66°W	43.64	-69	48.07	-66
ATS_1977_UTM_Zone_20N	2220	Canada - Maritime Provinces - east of 66°W	43.41	-66	47.98	-59.73
Austria_Central_Zone	31282	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
Austria_East_Zone	31283	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
Austria_West_Zone	31281	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
Azores_Central_1948_UTM_Zone_26N	2189	Portugal - Azores C - onshore	38.32	-28.9	39.14	-26.97
Azores_Central_1995_UTM_Zone_26N	3063	Portugal - Azores C - onshore	38.32	-28.9	39.14	-26.97
Azores_Occidental_1939_UTM_Zone_25 N	2188	Portugal - Azores W - onshore	39.3	-31.34	39.77	-31.02
Azores_Oriental_1940_UTM_Zone_26N	2190	Portugal - Azores E - onshore	36.87	-25.92	37.96	-24.62
Azores_Oriental_1995_UTM_Zone_26N	3062	Portugal - Azores E - onshore	36.87	-25.92	37.96	-24.62
Bab_South_Palau_Azimuthal_Equidistant	102096	Palau	1.64	129.48	11.45	136.98
Bahrain_State_Grid	20499	Bahrain - onshore	25.53	50.39	26.34	50.85
Barbados_1938_Barbados_Grid	21292	Barbados - onshore	13	-59.71	13.39	-59.37
Barbados_1938_British_West_Indies_ Grid	21291	Barbados - onshore	13	-59.71	13.39	-59.37
Batavia_Jakarta_NEIEZ	5330	Indonesia - Bali, Java and western Sumatra onshore	-8.91	95.16	5.97	115.77
Batavia_NEIEZ	3001	Indonesia - Bali, Java and western Sumatra onshore	-8.91	95.16	5.97	115.77
Batavia_TM_109_SE	2308	Indonesia - Java Sea - offshore northwest Java	-6.89	105.77	-4.07	110.01
Batavia_UTM_Zone_48S	21148	Indonesia - Java and Java Sea - west of 108°E	-7.79	105.06	-4.07	108
Batavia_UTM_Zone_49S	21149	Indonesia - Java and Java Sea - 108°E to 114°E	-8.67	108	-4.27	114
Batavia_UTM_Zone_50S	21150	Indonesia - Java and Java Sea - east of 114°E	-8.91	114	-5.33	117.01
Beduaram_TM_13_NE	2931	Niger - southeast	12.8	7.81	16.7	14.9
Beijing_1954_3_Degree_GK_CM_102E	2431	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
Beijing_1954_3_Degree_GK_CM_105E	2432	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
Beijing_1954_3_Degree_GK_CM_108E	2433	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
Beijing_1954_3_Degree_GK_CM_111E	2434	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
Beijing_1954_3_Degree_GK_CM_114E	2435	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
Beijing_1954_3_Degree_GK_CM_117E	2436	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
Beijing_1954_3_Degree_GK_CM_120E	2437	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
Beijing_1954_3_Degree_GK_CM_123E	2438	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
Beijing_1954_3_Degree_GK_CM_126E	2439	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
Beijing_1954_3_Degree_GK_CM_129E	2440	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
Beijing_1954_3_Degree_GK_CM_132E	2441	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
Beijing_1954_3_Degree_GK_CM_135E	2442	China - east of 133.5°E	45.85	133.5	48.4	134.77
Beijing_1954_3_Degree_GK_CM_75E	2422	China - west of 76.5°E	35.81	73.62	40.65	76.5
Beijing_1954_3_Degree_GK_CM_78E	2423	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
Beijing_1954_3_Degree_GK_CM_81E	2424	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
Beijing_1954_3_Degree_GK_CM_84E	2425	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
Beijing_1954_3_Degree_GK_CM_87E	2426	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
Beijing_1954_3_Degree_GK_CM_90E	2427	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
Beijing_1954_3_Degree_GK_CM_93E	2428	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
Beijing_1954_3_Degree_GK_CM_96E	2429	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
Beijing_1954_3_Degree_GK_CM_99E	2430	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
Beijing_1954_3_Degree_GK_Zone_25	2401	China - west of 76.5°E	35.81	73.62	40.65	76.5
Beijing_1954_3_Degree_GK_Zone_26	2402	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
Beijing_1954_3_Degree_GK_Zone_27	2403	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
Beijing_1954_3_Degree_GK_Zone_28	2404	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
Beijing_1954_3_Degree_GK_Zone_29	2405	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
Beijing_1954_3_Degree_GK_Zone_30	2406	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
Beijing_1954_3_Degree_GK_Zone_31	2407	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
Beijing_1954_3_Degree_GK_Zone_32	2408	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
Beijing_1954_3_Degree_GK_Zone_33	2409	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
Beijing_1954_3_Degree_GK_Zone_34	2410	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
Beijing_1954_3_Degree_GK_Zone_35	2411	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
Beijing_1954_3_Degree_GK_Zone_36	2412	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
Beijing_1954_3_Degree_GK_Zone_37	2413	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
Beijing_1954_3_Degree_GK_Zone_38	2414	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
Beijing_1954_3_Degree_GK_Zone_39	2415	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
Beijing_1954_3_Degree_GK_Zone_40	2416	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
Beijing_1954_3_Degree_GK_Zone_41	2417	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
Beijing_1954_3_Degree_GK_Zone_42	2418	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
Beijing_1954_3_Degree_GK_Zone_43	2419	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
Beijing_1954_3_Degree_GK_Zone_44	2420	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
Beijing_1954_3_Degree_GK_Zone_45	2421	China - east of 133.5°E	45.85	133.5	48.4	134.77
Beijing_1954_Gauss_Kruger_CM_105E	21458	China - 102°E to 108°E onshore	21.53	102	42.47	108
Beijing_1954_Gauss_Kruger_CM_111E	21459	China - 108°E to 114°E onshore	18.11	108	45.11	114
Beijing_1954_Gauss_Kruger_CM_117E	21460	China - 114°E to 120°E onshore	22.14	114	51.52	120
Beijing_1954_Gauss_Kruger_CM_123E	21461	China - 120°E to 126°E onshore	26.34	120	53.56	126
Beijing_1954_Gauss_Kruger_CM_129E	21462	China - 126°E to 132°E onshore	40.89	126	52.79	132
Beijing_1954_Gauss_Kruger_CM_135E	21463	China - east of 132°E	45.02	132	48.4	134.77
Beijing_1954_Gauss_Kruger_CM_75E	21453	China - west of 78°E	35.42	73.62	41.07	78.01
Beijing_1954_Gauss_Kruger_CM_81E	21454	China - 78°E to 84°E	29.16	77.98	47.23	84
Beijing_1954_Gauss_Kruger_CM_87E	21455	China - 84°E to 90°E	27.32	84	49.18	90
Beijing_1954_Gauss_Kruger_CM_93E	21456	China - 90°E to 96°E	27.71	90	47.9	96.01
Beijing_1954_Gauss_Kruger_CM_99E	21457	China - 96°E to 102°E	21.13	96	43.18	102.01
Beijing_1954_GK_Zone_13	21413	China - west of 78°E	35.42	73.62	41.07	78.01
Beijing_1954_GK_Zone_13N	21473	China - west of 78°E	35.42	73.62	41.07	78.01
Beijing_1954_GK_Zone_14	21414	China - 78°E to 84°E	29.16	77.98	47.23	84
Beijing_1954_GK_Zone_14N	21474	China - 78°E to 84°E	29.16	77.98	47.23	84
Beijing_1954_GK_Zone_15	21415	China - 84°E to 90°E	27.32	84	49.18	90
Beijing_1954_GK_Zone_15N	21475	China - 84°E to 90°E	27.32	84	49.18	90
Beijing_1954_GK_Zone_16	21416	China - 90°E to 96°E	27.71	90	47.9	96.01
Beijing_1954_GK_Zone_16N	21476	China - 90°E to 96°E	27.71	90	47.9	96.01
Beijing_1954_GK_Zone_17	21417	China - 96°E to 102°E	21.13	96	43.18	102.01
Beijing_1954_GK_Zone_17N	21477	China - 96°E to 102°E	21.13	96	43.18	102.01
Beijing_1954_GK_Zone_18	21418	China - 102°E to 108°E onshore	21.53	102	42.47	108
Beijing_1954_GK_Zone_18N	21478	China - 102°E to 108°E onshore	21.53	102	42.47	108
Beijing_1954_GK_Zone_19	21419	China - 108°E to 114°E onshore	18.11	108	45.11	114
Beijing_1954_GK_Zone_19N	21479	China - 108°E to 114°E onshore	18.11	108	45.11	114
Beijing_1954_GK_Zone_20	21420	China - 114°E to 120°E onshore	22.14	114	51.52	120
Beijing_1954_GK_Zone_20N	21480	China - 114°E to 120°E onshore	22.14	114	51.52	120
Beijing_1954_GK_Zone_21	21421	China - 120°E to 126°E onshore	26.34	120	53.56	126
Beijing_1954_GK_Zone_21N	21481	China - 120°E to 126°E onshore	26.34	120	53.56	126
Beijing_1954_GK_Zone_22	21422	China - 126°E to 132°E onshore	40.89	126	52.79	132
Beijing_1954_GK_Zone_22N	21482	China - 126°E to 132°E onshore	40.89	126	52.79	132
Beijing_1954_GK_Zone_23	21423	China - east of 132°E	45.02	132	48.4	134.77
Beijing_1954_GK_Zone_23N	21483	China - east of 132°E	45.02	132	48.4	134.77
Belge_Lambert_1950	21500	Belgium - onshore	49.5	2.5	51.51	6.4
Belge_Lambert_1972	31370	Belgium - onshore	49.5	2.5	51.51	6.4
Belge_Lambert_1972_bad_FE_FN	102499	Belgium - onshore	49.5	2.5	51.51	6.4
Belge_Lambert_2005	3447	Belgium - onshore	49.5	2.5	51.51	6.4
Belge_Lambert_2008	3812	Belgium - onshore	49.5	2.5	51.51	6.4
Berghaus_Star_AAG	102299	World	-90	-180	90	180
Bermuda_1957_UTM_Zone_20N	3769	Bermuda - onshore	32.21	-64.89	32.43	-64.61
Bermuda_2000_National_Grid	3770	Bermuda	28.91	-68.83	35.73	-60.7
Bern_1898_Bern_LV03C	21780	Europe - Liechtenstein and Switzerland	45.82	5.96	47.81	10.49
BGS2005_CCS2005	7801	Bulgaria - onshore	41.24	22.36	44.23	28.68
BGS2005_UTM_zone_34N	7803	Bulgaria - west of 24°E	41.32	22.36	44.23	24
BGS2005_UTM_zone_34N_(N-E)	7799	Bulgaria - west of 24°E	41.32	22.36	44.23	24
BGS2005_UTM_zone_35N	7804	Bulgaria - 24°E to 30°E	41.24	24	44.15	30.01
BGS2005_UTM_zone_35N_(N-E)	7800	Bulgaria - 24°E to 30°E	41.24	24	44.15	30.01
BGS2005_UTM_zone_36N	7805	Bulgaria - east of 30°E	42.56	30	43.67	31.35
Bissau_UTM_Zone_28N	2095	Guinea-Bissau - onshore	10.87	-16.77	12.69	-13.64
Bogota_Ciudad_Bogota	102232	Colombia region 8	-4.23	-74.4	7.1	-66.87
Bogota_UTM_Zone_17N	21817	Colombia - west of 75°35'W	0.03	-79.1	10.21	-75.58
Bogota_UTM_Zone_18N	21818	Colombia - offshore Caribbean west of 72°W	7.9	-77.37	13.68	-72
British_National_Grid	27700	UK - Britain and UKCS 49°46'N to 61°01'N, 7°33'W to 3°33'E	49.75	-9.2	61.14	2.88
BUTM2010	102954	Bangladesh	18.56	88.01	26.64	92.67
Cadastre_1997_UTM_Zone_38S	5879	Mayotte - onshore	-13.05	44.98	-12.61	45.35
Camacupa_TM_11_30_SE	22091	Angola - offshore block 15	-6.59	10.83	-6.03	11.67
Camacupa_TM_12_SE	22092	Angola - Angola proper - offshore	-17.26	8.2	-6.01	13.86
Camacupa_UTM_Zone_32S	22032	Angola - Angola proper - offshore - west of 12°E	-17.26	8.2	-6.03	12
Camacupa_UTM_Zone_33S	22033	Angola - Angola proper - 12°E to 18°E	-17.44	12	-5.82	18
Campo_Inchauspe_UTM_19S	2315	Argentina - Tierra del Fuego offshore west of 66°W	-54.61	-68.62	-51.65	-66
Campo_Inchauspe_UTM_20S	2316	Argentina - Tierra del Fuego offshore east of 66°W	-54.93	-66	-51.36	-61.49
Canada_Albers_Equal_Area_Conic	102001	Canada	38.21	-141.01	86.46	-40.73
Canada_Lambert_Conformal_Conic	102002	Canada	38.21	-141.01	86.46	-40.73
Cape_Lo15	102470	Namibia - Walvis Bay	-23.15	14.35	-22.68	14.6
Cape_Lo17	102471	South Africa - west of 18°E	-33.1	16.45	-28.03	18
Cape_Lo19	102472	South Africa - 18°E to 20°E	-34.88	17.99	-28.38	20
Cape_Lo21	102473	South Africa - 20°E to 22°E	-34.88	19.99	-24.76	22.01
Cape_Lo23	102474	South Africa - 22°E to 24°E	-34.26	22	-25.26	24.01
Cape_Lo25	102475	South Africa - 24°E to 26°E	-34.26	24	-24.71	26.01
Cape_Lo27	102476	South Africa - 26°E to 28°E	-33.83	26	-22.92	28
Cape_Lo29	102477	South Africa - 28°E to 30°E	-33.03	27.99	-22.13	30
Cape_Lo31	102478	South Africa - 30°E to 32°E	-31.38	29.99	-22.22	32.02
Cape_Lo33	102479	South Africa - east of 32°E	-28.94	31.95	-26.8	32.95
Cape_UTM_Zone_34S	22234	Botswana - west of 24°E	-26.88	19.99	-17.99	24
Cape_UTM_Zone_35S	22235	Botswana - east of 24°E	-25.84	24	-17.78	29.38
Cape_UTM_Zone_36S	22236	Botswana - 21°E to 27°E	-26.88	21	-17.78	27
Carthage_TM_11_NE	2088	Tunisia - offshore	33.22	7.81	38.41	13.67
Carthage_UTM_Zone_32N	22332	Tunisia - offshore	33.22	7.81	38.41	13.67
Cassini_Bangladesh_Zone_01_Dinajpur	102934	Bangladesh - Dinajpur	25.217	88.083	26.633	89.3
Cassini_Bangladesh_Zone_02_Rangpur	102935	Bangladesh - Rangpur	25.033	88.9	26.45	89.883
Cassini_Bangladesh_Zone_03_Rajshahi	102936	Bangladesh - Rajshahi	24.1	88	25.2	89.333
Cassini_Bangladesh_Zone_04_Bogura	102937	Bangladesh - Bogura	24.533	88.917	25.267	89.75
Cassini_Bangladesh_Zone_05_Pabna	102938	Bangladesh - Pabna	23.8	88.983	24.767	89.817
Cassini_Bangladesh_Zone_06_ Mymensingh	102939	Bangladesh - Mymensingh	23.95	89.633	24.433	91.25
Cassini_Bangladesh_Zone_07_Dhaka	102940	Bangladesh - Dhaka	23.367	89.683	24.333	90.983
Cassini_Bangladesh_Zone_08_Faridpur	102941	Bangladesh - Faridpur	22.833	89.283	23.9	89.583
Cassini_Bangladesh_Zone_09_Sylhet	102942	Bangladesh - Sylhet	23.967	90.917	25.2	92.483
Cassini_Bangladesh_Zone_10_Kushtia	102943	Bangladesh - Kushtia	23.367	88.55	24.217	89.35
Cassini_Bangladesh_Zone_11_Joshore	102944	Bangladesh - Joshore	22.783	88.683	23.767	89.8
Cassini_Bangladesh_Zone_12_Khulna	102945	Bangladesh - Khulna	21.633	88.883	23	89.95
Cassini_Bangladesh_Zone_13_Barishal	102946	Bangladesh - Barishal	21.783	89.85	23.067	91.033
Cassini_Bangladesh_Zone_14_Cumilla	102947	Bangladesh - Cumilla	22.967	90.517	24.267	91.367
Cassini_Bangladesh_Zone_15_Noakhali	102948	Bangladesh - Noakhali	22.017	90.65	23.283	91.567
Cassini_Bangladesh_Zone_16_ Chottogram	102949	Bangladesh - Chottogram	20.583	91.3	22.983	92.367
Cassini_Bangladesh_Zone_17_CHT	102950	Bangladesh - CHT	21.183	91.7	23.733	92.667
Cayman_Islands_National_Grid_2011	6391	Cayman Islands	17.58	-83.6	20.68	-78.72
CGCS2000_3_Degree_GK_CM_102E	4543	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
CGCS2000_3_Degree_GK_CM_105E	4544	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
CGCS2000_3_Degree_GK_CM_108E	4545	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
CGCS2000_3_Degree_GK_CM_111E	4546	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
CGCS2000_3_Degree_GK_CM_114E	4547	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
CGCS2000_3_Degree_GK_CM_117E	4548	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
CGCS2000_3_Degree_GK_CM_120E	4549	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
CGCS2000_3_Degree_GK_CM_123E	4550	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
CGCS2000_3_Degree_GK_CM_126E	4551	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
CGCS2000_3_Degree_GK_CM_129E	4552	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
CGCS2000_3_Degree_GK_CM_132E	4553	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
CGCS2000_3_Degree_GK_CM_135E	4554	China - east of 133.5°E	45.85	133.5	48.4	134.77
CGCS2000_3_Degree_GK_CM_75E	4534	China - west of 76.5°E	35.81	73.62	40.65	76.5
CGCS2000_3_Degree_GK_CM_78E	4535	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
CGCS2000_3_Degree_GK_CM_81E	4536	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
CGCS2000_3_Degree_GK_CM_84E	4537	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
CGCS2000_3_Degree_GK_CM_87E	4538	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
CGCS2000_3_Degree_GK_CM_90E	4539	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
CGCS2000_3_Degree_GK_CM_93E	4540	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
CGCS2000_3_Degree_GK_CM_96E	4541	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
CGCS2000_3_Degree_GK_CM_99E	4542	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
CGCS2000_3_Degree_GK_Zone_25	4513	China - west of 76.5°E	35.81	73.62	40.65	76.5
CGCS2000_3_Degree_GK_Zone_26	4514	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
CGCS2000_3_Degree_GK_Zone_27	4515	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
CGCS2000_3_Degree_GK_Zone_28	4516	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
CGCS2000_3_Degree_GK_Zone_29	4517	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
CGCS2000_3_Degree_GK_Zone_30	4518	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
CGCS2000_3_Degree_GK_Zone_31	4519	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
CGCS2000_3_Degree_GK_Zone_32	4520	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
CGCS2000_3_Degree_GK_Zone_33	4521	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
CGCS2000_3_Degree_GK_Zone_34	4522	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
CGCS2000_3_Degree_GK_Zone_35	4523	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
CGCS2000_3_Degree_GK_Zone_36	4524	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
CGCS2000_3_Degree_GK_Zone_37	4525	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
CGCS2000_3_Degree_GK_Zone_38	4526	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
CGCS2000_3_Degree_GK_Zone_39	4527	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
CGCS2000_3_Degree_GK_Zone_40	4528	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
CGCS2000_3_Degree_GK_Zone_41	4529	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
CGCS2000_3_Degree_GK_Zone_42	4530	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
CGCS2000_3_Degree_GK_Zone_43	4531	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
CGCS2000_3_Degree_GK_Zone_44	4532	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
CGCS2000_3_Degree_GK_Zone_45	4533	China - east of 133.5°E	45.85	133.5	48.4	134.77
CGCS2000_GK_CM_105E	4507	China - 102°E to 108°E	17.75	102	42.47	108
CGCS2000_GK_CM_111E	4508	China - 108°E to 114°E	16.7	108	45.11	114
CGCS2000_GK_CM_117E	4509	China - 114°E to 120°E	19.02	114	51.52	120
CGCS2000_GK_CM_123E	4510	China - 120°E to 126°E	24.64	120	53.56	126
CGCS2000_GK_CM_129E	4511	China - 126°E to 132°E	29.7	126	52.79	132
CGCS2000_GK_CM_135E	4512	China - east of 132°E	45.02	132	48.4	134.77
CGCS2000_GK_CM_75E	4502	China - west of 78°E	35.42	73.62	41.07	78.01
CGCS2000_GK_CM_81E	4503	China - 78°E to 84°E	29.16	77.98	47.23	84
CGCS2000_GK_CM_87E	4504	China - 84°E to 90°E	27.32	84	49.18	90
CGCS2000_GK_CM_93E	4505	China - 90°E to 96°E	27.71	90	47.9	96.01
CGCS2000_GK_CM_99E	4506	China - 96°E to 102°E	21.13	96	43.18	102.01
CGCS2000_GK_Zone_13	4491	China - west of 78°E	35.42	73.62	41.07	78.01
CGCS2000_GK_Zone_14	4492	China - 78°E to 84°E	29.16	77.98	47.23	84
CGCS2000_GK_Zone_15	4493	China - 84°E to 90°E	27.32	84	49.18	90
CGCS2000_GK_Zone_16	4494	China - 90°E to 96°E	27.71	90	47.9	96.01
CGCS2000_GK_Zone_17	4495	China - 96°E to 102°E	21.13	96	43.18	102.01
CGCS2000_GK_Zone_18	4496	China - 102°E to 108°E	17.75	102	42.47	108
CGCS2000_GK_Zone_19	4497	China - 108°E to 114°E	16.7	108	45.11	114
CGCS2000_GK_Zone_20	4498	China - 114°E to 120°E	19.02	114	51.52	120
CGCS2000_GK_Zone_21	4499	China - 120°E to 126°E	24.64	120	53.56	126
CGCS2000_GK_Zone_22	4500	China - 126°E to 132°E	29.7	126	52.79	132
CGCS2000_GK_Zone_23	4501	China - east of 132°E	45.02	132	48.4	134.77
CGRS_1993_Cyprus_Local_Transverse_ Mercator	6312	Cyprus - onshore	34.59	32.2	35.74	34.65
CGRS_1993_LTM	102319	Cyprus - onshore	34.59	32.2	35.74	34.65
CH1903+_LV95	2056	Europe - Liechtenstein and Switzerland	45.82	5.96	47.81	10.49
CH1903_LV03	21781	Europe - Liechtenstein and Switzerland	45.82	5.96	47.81	10.49
CH1903_LV03C-G	21782	Liechtenstein	47.05	9.47	47.28	9.64
Chatham_Island_1971_Map_Grid	5518	New Zealand - Chatham Islands group	-44.64	-177.25	-43.3	-175.54
Chatham_Islands_1979_Map_Grid	5519	New Zealand - Chatham Islands group	-44.64	-177.25	-43.3	-175.54
Chos_Malal_1914_Argentina_2	2081	Argentina - Mendoza and Neuquen 70.5°W to 67.5°W	-43.41	-70.51	-31.91	-67.49
Chua_UTM_Zone_23S	4071	Brazil - Distrito Federal	-15.94	-48.1	-15.37	-47.1
COB_NAD83_2007	102041	USA - Washington - Bellevue	47.5	-122.26	47.69	-122.06
Colombia_Bogota_Zone	21897	Colombia - 75°35'W to 72°35'W	-2.51	-75.59	11.82	-72.58
Colombia_East_Central_Zone	21898	Colombia - 72°35'W to 69°35'W	-4.23	-72.59	12.52	-69.58
Colombia_East_Zone	21899	Colombia - east of 69°35'W	-2.25	-69.59	6.31	-66.87
Colombia_West_West_Zone	102231	Colombia - west of 78°35'W	1.23	-79.1	2.48	-78.58
Colombia_West_Zone	21896	Colombia - west of 75°35'W	0.03	-79.1	10.21	-75.58
Combani_1950_UTM_38S	2980	Mayotte - onshore	-13.05	44.98	-12.61	45.35
Conakry_1905_UTM_Zone_28N	31528	Guinea - west of 12°W	9.01	-15.13	12.68	-12
Conakry_1905_UTM_Zone_29N	31529	Guinea - east of 12°W	7.19	-12	12.51	-7.65
Corrego_Alegre_1961_UTM_Zone_21S	5536	Brazil - west of 54°W and south of 18°S	-31.91	-58.16	-17.99	-54
Corrego_Alegre_1961_UTM_Zone_22S	5537	Brazil - 54°W to 48°W and south of 15°S	-33.78	-54	-15	-48
Corrego_Alegre_1961_UTM_Zone_23S	5538	Brazil - 48°W to 42°W and south of 15°S	-25.29	-48	-15	-42
Corrego_Alegre_1961_UTM_Zone_24S	5539	Brazil - 42°W to 36°W and south of 15°S onshore	-22.96	-42	-14.99	-38.82
Corrego_Alegre_UTM_Zone_21S	22521	Brazil - west of 54°W and south of 18°S	-31.91	-58.16	-17.99	-54
Corrego_Alegre_UTM_Zone_22S	22522	Brazil - 54°W to 48°W and south of 15°S	-33.78	-54	-15	-48
Corrego_Alegre_UTM_Zone_23S	22523	Brazil - 48°W to 42°W and south of 15°S	-25.29	-48	-15	-42
Corrego_Alegre_UTM_Zone_24S	22524	Brazil - 42°W to 36°W onshore	-22.96	-42	-2.68	-36
Corrego_Alegre_UTM_Zone_25S	22525	Brazil - east of 36°W onshore	-10.1	-36	-4.99	-34.74
CR-SIRGAS_CRTM05	8908	Costa Rica - onshore	7.98	-85.97	11.22	-82.53
CR-SIRGAS_UTM_Zone_16N	8909	Costa Rica - offshore Pacific	2.15	-90.45	11.11	-82.92
CR-SIRGAS_UTM_Zone_17N	8910	Costa Rica - offshore Caribbean	9.6	-83.6	11.77	-81.43
CRTM05	5367	Costa Rica - onshore and offshore east of 86°30'W	2.21	-86.5	11.77	-81.43
CSG_1967_UTM_22N	2971	French Guiana - coastal area east of 54°W	3.43	-54	5.81	-51.61
CSG_1967_UTM_Zone_21N	3312	French Guiana - coastal area west of 54°W	4.84	-54.45	5.69	-54
D48_Slovenia_TM	102060	Slovenia	45.42	13.38	46.88	16.61
Dabola_1981_UTM_Zone_28N	3461	Guinea - west of 12°W	9.01	-15.13	12.68	-12
Dabola_1981_UTM_Zone_29N	3462	Guinea - east of 12°W	7.19	-12	12.51	-7.65
Datum_73_Hayford_Gauss_IGeoE	102160	Portugal	29.24	-35.58	43.07	-6.19
Datum_73_Hayford_Gauss_IPCC	102161	Portugal	29.24	-35.58	43.07	-6.19
Datum_73_Modified_Portuguese_Grid	27493	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
Datum_73_UTM_Zone_29N	27429	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
DB_REF_3-Degree_GK_Zone_2_(E-N)	5682	Germany - West Germany - west of 7.5°E	49.11	5.86	53.81	7.5
DB_REF_3-Degree_GK_Zone_3_(E-N)	5683	Germany - onshore 7.5°E to 10.5°E	47.27	7.5	55.09	10.51
DB_REF_3-Degree_GK_Zone_4_(E-N)	5684	Germany - onshore 10.5°E to 13.5°E	47.39	10.5	54.74	13.51
DB_REF_3-Degree_GK_Zone_5_(E-N)	5685	Germany - onshore east of 13.5°E	48.51	13.5	54.72	15.04
Deir_ez_Zor_Levant_Stereographic	22780	Asia - Middle East - Lebanon and Syria onshore	32.31	35.04	37.3	42.38
Deir_ez_Zor_Levant_Zone	22700	Asia - Middle East - Lebanon and Syria onshore	32.31	35.04	37.3	42.38
Deir_ez_Zor_Syria_Lambert	22770	Asia - Middle East - Lebanon and Syria onshore	32.31	35.04	37.3	42.38
DGN_1995_Indonesia_TM-3_Zone_46.2	23830	Indonesia - west of 96°E onshore	2.55	95.16	5.97	96
DGN_1995_Indonesia_TM-3_Zone_47.1	23831	Indonesia - 96°E to 99°E onshore	-1.81	96	5.42	99
DGN_1995_Indonesia_TM-3_Zone_47.2	23832	Indonesia - 99°E to 102°E onshore	-3.57	99	3.71	102
DGN_1995_Indonesia_TM-3_Zone_48.1	23833	Indonesia - 102°E to 105°E onshore	-5.99	102	1.68	105
DGN_1995_Indonesia_TM-3_Zone_48.2	23834	Indonesia - 105°E to 108°E onshore	-7.79	105	4.11	108
DGN_1995_Indonesia_TM-3_Zone_49.1	23835	Indonesia - 108°E to 111°E onshore	-8.31	108	4.25	111
DGN_1995_Indonesia_TM-3_Zone_49.2	23836	Indonesia - 111°E to 114°E onshore	-8.67	111	1.59	114
DGN_1995_Indonesia_TM-3_Zone_50.1	23837	Indonesia - 114°E to 117°E onshore	-9.15	114	4.37	117.01
DGN_1995_Indonesia_TM-3_Zone_50.2	23838	Indonesia - 117°E to 120°E onshore	-10.15	117	4.36	120
DGN_1995_Indonesia_TM-3_Zone_51.1	23839	Indonesia - 120°E to 123°E onshore	-10.98	120	1.4	123
DGN_1995_Indonesia_TM-3_Zone_51.2	23840	Indonesia - 123°E to 126°E onshore	-10.92	123	3.84	126
DGN_1995_Indonesia_TM-3_Zone_52.1	23841	Indonesia - 126°E to 129°E onshore	-8.32	126	4.59	129
DGN_1995_Indonesia_TM-3_Zone_52.2	23842	Indonesia - 129°E to 132°E onshore	-8.41	129	0.1	132
DGN_1995_Indonesia_TM-3_Zone_53.1	23843	Indonesia - 132°E to 135°E onshore	-7.3	132	-0.29	135
DGN_1995_Indonesia_TM-3_Zone_53.2	23844	Indonesia - 135°E to 138°E onshore	-8.49	135	-0.58	138
DGN_1995_Indonesia_TM-3_Zone_54.1	23845	Indonesia - east of 138°E onshore	-9.19	138	-1.49	141.01
DGN_1995_UTM_Zone_46N	23866	Indonesia - west of 96°E, N hemisphere	0	92.01	7.79	96
DGN_1995_UTM_Zone_47N	23867	Indonesia - 96°E to 102°E, N hemisphere	0	96	7.49	102
DGN_1995_UTM_Zone_47S	23877	Indonesia - 96°E to 102°E, S hemisphere	-8.86	96	0	102
DGN_1995_UTM_Zone_48N	23868	Indonesia - 102°E to 108°E, N hemisphere	0	102	6.94	108
DGN_1995_UTM_Zone_48S	23878	Indonesia - 102°E to 108°E, S hemisphere	-10.1	102	0	108.01
DGN_1995_UTM_Zone_49N	23869	Indonesia - 108°E to 114°E, N hemisphere	0	108	7.37	114
DGN_1995_UTM_Zone_49S	23879	Indonesia - 108°E to 114°E, S hemisphere	-12.07	108	0	114
DGN_1995_UTM_Zone_50N	23870	Indonesia - 114°E to 120°E, N hemisphere	0	114	4.37	120
DGN_1995_UTM_Zone_50S	23880	Indonesia - 114°E to 120°E, S hemisphere	-13.06	114	0	120.01
DGN_1995_UTM_Zone_51N	23871	Indonesia - 120°E to 126°E, N hemisphere	0	120	5.48	126
DGN_1995_UTM_Zone_51S	23881	Indonesia - 120°E to 126°E, S hemisphere	-13.95	120	0.01	126.01
DGN_1995_UTM_Zone_52N	23872	Indonesia - 126°E to 132°E, N hemisphere	0	126	6.68	132
DGN_1995_UTM_Zone_52S	23882	Indonesia - 126°E to 132°E, S hemisphere	-9.45	126	0	132
DGN_1995_UTM_Zone_53S	23883	Indonesia - 132°E to 138°E, S hemisphere	-10.06	132	0	138.01
DGN_1995_UTM_Zone_54S	23884	Indonesia - east of 138°E, S hemisphere	-10.84	138	0	141.46
DHDN_3_Degree_Gauss_Zone_1	5520	Germany - offshore North Sea west of 4.5°E	55.24	3.34	55.92	4.5
DHDN_3_Degree_Gauss_Zone_2	31466	Germany - West Germany - west of 7.5°E	49.11	5.86	53.81	7.5
DHDN_3_Degree_Gauss_Zone_3	31467	Germany - West- Germany - 7.5°E to 10.5°E	47.27	7.5	55.09	10.51
DHDN_3_Degree_Gauss_Zone_4	31468	Germany - West Germany - 10.5°E to 13.5°E	47.39	10.5	54.59	13.51
DHDN_3_Degree_Gauss_Zone_5	31469	Germany - West Germany - east of 13.5°E	48.51	13.5	48.98	13.84
DHDN_3_Degree_GK_Zone_1_E-N	5680	Germany - offshore North Sea west of 4.5°E	55.24	3.34	55.92	4.5
DHDN_3_Degree_GK_Zone_2_E-N	5676	Germany - West Germany - west of 7.5°E	49.11	5.86	53.81	7.5
DHDN_3_Degree_GK_Zone_3_E-N	5677	Germany - West- Germany - 7.5°E to 10.5°E	47.27	7.5	55.09	10.51
DHDN_3_Degree_GK_Zone_4_E-N	5678	Germany - West Germany - 10.5°E to 13.5°E	47.39	10.5	54.59	13.51
DHDN_3_Degree_GK_Zone_5_E-N	5679	Germany - West Germany - east of 13.5°E	48.51	13.5	48.98	13.84
DHDN_Soldner_Berlin	3068	Germany - Berlin	52.33	13.09	52.65	13.76
Dominica_1945_British_West_Indies_ Grid	2002	Dominica - onshore	15.14	-61.55	15.69	-61.2
Douala_1948_AEF_West	3119	Cameroon - coastal area	2.16	8.45	4.99	10.4
Douala_UTM_Zone_32N	22832	Cameroon	1.65	8.32	13.09	16.21
DRUKREF_03_Bhutan_National_Grid	5266	Bhutan	26.7	88.74	28.33	92.13
DRUKREF_03_Bumthang_TM	5292	Bhutan - Bumthang district	27.33	90.46	28.09	91.02
DRUKREF_03_Chhukha_TM	5293	Bhutan - Chhukha district	26.71	89.26	27.32	89.83
DRUKREF_03_Dagana_TM	5294	Bhutan - Dagana district	26.7	89.63	27.29	90.08
DRUKREF_03_Gasa_TM	5295	Bhutan - Gasa district	27.72	89.44	28.33	90.47
DRUKREF_03_Ha_TM	5296	Bhutan - Ha district	27.02	88.9	27.62	89.39
DRUKREF_03_Lhuentse_TM	5297	Bhutan - Lhuentse district	27.39	90.77	28.09	91.49
DRUKREF_03_Mongar_TM	5298	Bhutan - Mongar district	26.93	90.95	27.61	91.5
DRUKREF_03_Paro_TM	5299	Bhutan - Paro district	27.18	89.12	27.79	89.56
DRUKREF_03_Pemagatshel_TM	5300	Bhutan - Pemagatshel district	26.78	91	27.18	91.56
DRUKREF_03_Punakha_TM	5301	Bhutan - Punakha district	27.46	89.63	27.87	90.08
DRUKREF_03_Samdrup_Jongkhar_TM	5302	Bhutan - Samdrup Jongkhar district	26.79	91.39	27.25	92.13
DRUKREF_03_Samtse_TM	5303	Bhutan - Samtse district	26.8	88.74	27.28	89.38
DRUKREF_03_Sarpang_TM	5304	Bhutan - Sarpang district	26.73	90.01	27.23	90.78
DRUKREF_03_Thimphu_TM	5305	Bhutan - Thimphu district	27.14	89.22	28.01	89.77
DRUKREF_03_Trashigang_TM	5306	Bhutan - Trashigang district	27.01	91.37	27.49	92.13
DRUKREF_03_Trongsa_TM	5307	Bhutan - Trongsa district	27.13	90.26	27.79	90.76
DRUKREF_03_Tsirang_TM	5308	Bhutan - Tsirang district	26.81	90	27.2	90.35
DRUKREF_03_Wangdue_Phodrang_TM	5309	Bhutan - Wangdue Phodrang district	27.11	89.71	28.08	90.54
DRUKREF_03_Yangtse_TM	5310	Bhutan - Yangtse district	27.37	91.34	28	91.77
DRUKREF_03_Zhemgang_TM	5311	Bhutan - Zhemgang district	26.77	90.53	27.39	91.19
ECML14_NB_Grid	9761	UK - Newcastle to Ashington	54.85	-1.9	55.3	-1.3
ED_1950_3_Degree_GK_Zone_10	2207	Turkey - 28.5°E to 31.5°E onshore	36.06	28.5	41.46	31.5
ED_1950_3_Degree_GK_Zone_11	2208	Turkey - 31.5°E to 34.5°E onshore	35.97	31.5	42.07	34.5
ED_1950_3_Degree_GK_Zone_12	2209	Turkey - 34.5°E to 37.5°E onshore	35.81	34.5	42.15	37.5
ED_1950_3_Degree_GK_Zone_13	2210	Turkey - 37.5°E to 40.5°E onshore	36.66	37.5	41.19	40.5
ED_1950_3_Degree_GK_Zone_14	2211	Turkey - 40.5°E to 43.5°E onshore	37.02	40.5	41.6	43.5
ED_1950_3_Degree_GK_Zone_15	2212	Turkey - east of 43.5°E	36.97	43.5	41.02	44.83
ED_1950_3_Degree_GK_Zone_9	2206	Turkey - west of 28.5°E onshore	36.5	25.62	42.11	28.5
ED_1950_ED77_UTM_Zone_38N	2058	Iran - west of 48°E	30.99	44.03	39.78	48
ED_1950_ED77_UTM_Zone_39N	2059	Iran - 48°E to 54°E	25.47	48	39.71	54
ED_1950_ED77_UTM_Zone_40N	2060	Iran - 54°E to 60°E	25.32	54	38.29	60
ED_1950_ED77_UTM_Zone_41N	2061	Iran - east of 60°E onshore	25.02	60	37.06	63.34
ED_1950_France_EuroLambert	2192	France - mainland onshore	42.33	-4.87	51.14	8.23
ED_1950_Iraq_National_Grid	3893	Iraq - onshore	29.06	38.79	37.39	48.61
ED_1950_Jordan_TM	3066	Jordan	29.18	34.88	33.38	39.31
ED_1950_Southern_Permian_Basin_ Lambert	5643	Europe - South Permian basin	50.5	-1.67	56	22
ED_1950_TM_0_N	23090	UK - offshore - North Sea	51.03	-5.05	62.03	3.4
ED_1950_TM27	2319	Turkey - west of 28.5°E onshore	36.5	25.62	42.11	28.5
ED_1950_TM30	2320	Turkey - 28.5°E to 31.5°E onshore	36.06	28.5	41.46	31.5
ED_1950_TM33	2321	Turkey - 31.5°E to 34.5°E onshore	35.97	31.5	42.07	34.5
ED_1950_TM36	2322	Turkey - 34.5°E to 37.5°E onshore	35.81	34.5	42.15	37.5
ED_1950_TM39	2323	Turkey - 37.5°E to 40.5°E onshore	36.66	37.5	41.19	40.5
ED_1950_TM42	2324	Turkey - 40.5°E to 43.5°E onshore	37.02	40.5	41.6	43.5
ED_1950_TM45	2325	Turkey - east of 43.5°E	36.97	43.5	41.02	44.83
ED_1950_TM_5_NE	23095	Netherlands - offshore	51.45	2.53	55.77	6.41
ED_1950_TM_6_NE	5627	France - offshore Mediterranean	41.15	3.04	43.74	10.38
ED_1950_Turkey_10	102551	Turkey - 28.5°E to 31.5°E onshore	36.06	28.5	41.46	31.5
ED_1950_Turkey_11	102552	Turkey - 31.5°E to 34.5°E onshore	35.97	31.5	42.07	34.5
ED_1950_Turkey_12	102553	Turkey - 34.5°E to 37.5°E onshore	35.81	34.5	42.15	37.5
ED_1950_Turkey_13	102554	Turkey - 37.5°E to 40.5°E onshore	36.66	37.5	41.19	40.5
ED_1950_Turkey_14	102555	Turkey - 40.5°E to 43.5°E onshore	37.02	40.5	41.6	43.5
ED_1950_Turkey_15	102556	Turkey - east of 43.5°E	36.97	43.5	41.02	44.83
ED_1950_Turkey_9	102550	Turkey - west of 28.5°E onshore	36.5	25.62	42.11	28.5
ED_1950_UTM_Zone_28N	23028	Europe - 18°W to 12°W and ED50 by country	48.43	-16.1	56.57	-12
ED_1950_UTM_Zone_29N	23029	Europe - 12°W to 6°W and ED50 by country	36.13	-12	62.41	-6
ED_1950_UTM_Zone_30N	23030	Europe - 6°W to 0°W and ED50 by country	35.26	-6	80.49	0.01
ED_1950_UTM_Zone_31N	23031	Europe - 0°E to 6°E and ED50 by country	38.56	0	82.45	6.01
ED_1950_UTM_Zone_32N	23032	Europe - 6°E to 12°E and ED50 by country	36.53	5.99	84.33	12
ED_1950_UTM_Zone_33N	23033	Europe - 12°E to 18°E and ED50 by country	34.49	12	84.42	18
ED_1950_UTM_Zone_34N	23034	Europe - 18°E to 24°E and ED50 by country	33.59	18	84.54	24.01
ED_1950_UTM_Zone_35N	23035	Europe - 24°E to 30°E and ED50 by country	25.71	24	84.73	30.01
ED_1950_UTM_Zone_36N	23036	Europe - 30°E to 36°E and ED50 by country	29.19	30	84.7	36
ED_1950_UTM_Zone_37N	23037	Europe - 36°E to 42°E and ED50 by country	29.18	36	79.07	42
ED_1950_UTM_Zone_38N	23038	Europe - 42°E to 48°E and ED50 by country	36.97	42	41.6	44.83
Egypt_Blue_Belt	22991	Egypt - east of 33°E onshore	21.97	33	31.36	36.95
Egypt_Extended_Purple_Belt	22994	Egypt - west of 29°E; south of 28°11'N	21.99	24.99	28.19	29.01
Egypt_Gulf_of_Suez_S-650_TL_Red_Belt	3355	Egypt - Gulf of Suez	27.19	32.34	30.01	34.27
Egypt_Purple_Belt	22993	Egypt - west of 29°E; north of 28°11'N	28.18	24.7	31.68	29
Egypt_Red_Belt	22992	Egypt - 29°E to 33°E	21.99	29	33.82	34.27
ELD_1979_Libya_10	2073	Libya - 18°E to 20°E onshore	21.54	18	32.17	20
ELD_1979_Libya_11	2074	Libya - 20°E to 22°E onshore	20.54	20	33	22
ELD_1979_Libya_12	2075	Libya - 22°E to 24°E onshore	19.5	22	32.97	24
ELD_1979_Libya_13	2076	Libya - east of 24°E onshore	19.99	24	32.15	25.21
ELD_1979_Libya_5	2068	Libya - west of 10°E	25.37	9.31	30.49	10.01
ELD_1979_Libya_6	2069	Libya - 10°E to 12°E onshore	23.51	10	33.23	12
ELD_1979_Libya_7	2070	Libya - 12°E to 14°E onshore	22.8	12	33.06	14
ELD_1979_Libya_8	2071	Libya - 14°E to 16°E onshore	22.61	14	32.79	16
ELD_1979_Libya_9	2072	Libya - 16°E to 18°E onshore	22.51	16	31.34	18.01
ELD_1979_TM_12_NE	2087	Libya - west of 15°E onshore	22.61	9.31	33.23	15
ELD_1979_UTM_Zone_32N	2077	Libya - west of 12°E onshore	23.51	9.31	33.23	12
ELD_1979_UTM_Zone_33N	2078	Libya - 12°E to 18°E onshore	22.51	12	33.06	18.01
ELD_1979_UTM_Zone_34N	2079	Libya - 18°E to 24°E onshore	19.5	17.99	33	24
ELD_1979_UTM_Zone_35N	2080	Libya - east of 24°E onshore	19.99	24	32.15	25.21
EMEP_150_Kilometer_Grid	102069	Europe	34	-30	85	50
EMEP_50_Kilometer_Grid	102068	Europe	34	-30	85	50
EOS21_Grid	9741	UK - Tweedmouth to Aberdeen	55.55	-3.55	57.2	-1.95
Estonia_1997_Estonia_National_Grid	3301	Estonia	57.52	20.37	60	28.2
Estonian_Coordinate_System_of_1992	3300	Estonia - onshore	57.52	21.74	59.75	28.2
ETRS_1989_Albania_2010	6870	Albania - onshore	39.64	19.22	42.67	21.06
ETRS_1989_Albania_LCC_2010	6962	Albania - onshore	39.64	19.22	42.67	21.06
ETRS_1989_Austria_Lambert	3416	Austria	46.4	9.53	49.02	17.17
ETRS_1989_DKTM1	4093	Denmark - onshore Jutland west of 10°E	54.8	8	57.64	10
ETRS_1989_DKTM2	4094	Denmark - onshore Jutland east of 9°E and Funen	54.67	9	57.8	11.29
ETRS_1989_DKTM3	4095	Denmark - onshore Zealand and Lolland	54.51	10.79	56.79	12.69
ETRS_1989_DKTM4	4096	Denmark - onshore Bornholm	54.94	14.59	55.38	15.25
ETRS_1989_EPSG_Arctic_zone_2-22	6069	Arctic - 84°30'N to 79°30'N, 4°W to 36°E	79.5	-4	84.51	36.01
ETRS_1989_EPSG_Arctic_zone_3-11	6070	Arctic - 81°10'N to 76°10'N, 4°W to 38°E	76.16	-3.35	81.17	38
ETRS_1989_EPSG_Arctic_zone_4-26	6071	Arctic - 77°50'N to 72°50'N, 2°W to 22°E	72.83	-2	77.84	22.01
ETRS_1989_EPSG_Arctic_zone_4-28	6072	Arctic - 77°50'N to 72°50'N, 22°E to 46°E	72.83	22	77.84	46.01
ETRS_1989_EPSG_Arctic_zone_5-11	6073	Arctic - 74°30'N to 69°30'N, 4°E to 24°E	69.5	4	74.51	24.01
ETRS_1989_EPSG_Arctic_zone_5-13	6074	Arctic - 74°30'N to 69°30'N, 24°E to 44°E	69.5	24	74.51	44.01
ETRS_1989_EPSG_Arctic_zone_5-47	6125	Arctic - 74°30'N to 69°30'N, 15°W to 5°E	69.5	-15	74.51	5.01
ETRS_1989_ETRS-GK19FIN	3126	Finland - west of 19.5°E onshore	60.08	19.24	60.34	19.5
ETRS_1989_ETRS-GK20FIN	3127	Finland - 19.5°E to 20.5°E onshore	59.92	19.5	60.48	20.5
ETRS_1989_ETRS-GK21FIN	3128	Finland - 20.5°E to 21.5°E onshore	59.84	20.5	69.33	21.5
ETRS_1989_ETRS-GK22FIN	3129	Finland - 21.5°E to 22.5°E onshore	59.76	21.5	69.31	22.5
ETRS_1989_ETRS-GK23FIN	3130	Finland - 22.5°E to 23.5°E onshore	59.75	22.5	68.74	23.5
ETRS_1989_ETRS-GK24FIN	3131	Finland - 23.5°E to 24.5°E onshore	59.86	23.5	68.84	24.5
ETRS_1989_ETRS-GK25FIN	3132	Finland - 24.5°E to 25.5°E onshore	59.94	24.5	68.9	25.5
ETRS_1989_ETRS-GK26FIN	3133	Finland - 25.5°E to 26.5°E onshore	60.18	25.5	69.94	26.5
ETRS_1989_ETRS-GK27FIN	3134	Finland - 26.5°E to 27.5°E onshore	60.36	26.5	70.05	27.5
ETRS_1989_ETRS-GK28FIN	3135	Finland - 27.5°E to 28.5°E onshore	60.42	27.5	70.09	28.5
ETRS_1989_ETRS-GK29FIN	3136	Finland - 28.5°E to 29.5°E	60.94	28.5	69.81	29.5
ETRS_1989_ETRS-GK30FIN	3137	Finland - 29.5°E to 30.5°E	61.43	29.5	67.98	30.5
ETRS_1989_ETRS-GK31FIN	3138	Finland - east of 30.5°E	62.08	30.5	64.27	31.59
ETRS_1989_ETRS-TM26	3038	Europe - 30°W to 24°W	25.1	-30	65.8	-24
ETRS_1989_ETRS-TM27	3039	Europe - 24°W to 18°W	27.6	-24	66.5	-18
ETRS_1989_ETRS-TM28	3040	Europe - 18°W to 12°W and ETRS89 by country	34.93	-16.1	72.44	-11.99
ETRS_1989_ETRS-TM29	3041	Europe - 12°W to 6°W and ETRS89 by country	34.91	-12	74.13	-6
ETRS_1989_ETRS-TM30	3042	Europe - 6°W to 0°W and ETRS89 by country	35.26	-6	80.49	0.01
ETRS_1989_ETRS-TM31	3043	Germany - west of 6°E	50.97	3.34	55.92	6
ETRS_1989_ETRS-TM32	3044	Germany - 6°E to 12°E	47.27	6	55.47	12
ETRS_1989_ETRS-TM33	3045	Germany - east of 12°E	47.46	11.57	55.03	15.04
ETRS_1989_ETRS-TM34	3046	Europe - 18°E to 24°E and ETRS89 by country	58.84	18	84.54	24.01
ETRS_1989_ETRS-TM35	3047	Europe - 24°E to 30°E and ETRS89 by country	59.64	24	84.73	30.01
ETRS_1989_ETRS-TM36	3048	Europe - 30°E to 36°E and ETRS89 by country	61.73	30	84.7	36
ETRS_1989_ETRS-TM37	3049	Europe - 36°E to 42°E and ETRS89 by country	72.99	36	79.07	38
ETRS_1989_ETRS-TM38	3050	Europe - 42°E to 48°E	36.95	42	75	48
ETRS_1989_ETRS-TM39	3051	Europe - 48°E to 54°E	36	48	75	54
ETRS_1989_FAROE_TM	5316	Faroe Islands	59.94	-13.91	65.7	-0.48
ETRS_1989_GK_CM_9E	8395	Germany - Hamburg	53.36	8.33	53.99	10.41
ETRS_1989_GK19FIN	3873	Finland - west of 19.5°E onshore nominal	60.08	19.24	60.34	19.5
ETRS_1989_GK20FIN	3874	Finland - 19.5°E to 20.5°E onshore nominal	59.92	19.5	60.48	20.5
ETRS_1989_GK21FIN	3875	Finland - 20.5°E to 21.5°E onshore nominal	59.84	20.5	69.33	21.5
ETRS_1989_GK22FIN	3876	Finland - 21.5°E to 22.5°E onshore nominal	59.76	21.5	69.31	22.5
ETRS_1989_GK23FIN	3877	Finland - 22.5°E to 23.5°E onshore nominal	59.75	22.5	68.74	23.5
ETRS_1989_GK24FIN	3878	Finland - 23.5°E to 24.5°E onshore nominal	59.86	23.5	68.84	24.5
ETRS_1989_GK25FIN	3879	Finland - 24.5°E to 25.5°E onshore nominal	59.94	24.5	68.9	25.5
ETRS_1989_GK26FIN	3880	Finland - 25.5°E to 26.5°E onshore nominal	60.18	25.5	69.94	26.5
ETRS_1989_GK27FIN	3881	Finland - 26.5°E to 27.5°E onshore nominal	60.36	26.5	70.05	27.5
ETRS_1989_GK28FIN	3882	Finland - 27.5°E to 28.5°E onshore nominal	60.42	27.5	70.09	28.5
ETRS_1989_GK29FIN	3883	Finland - 28.5°E to 29.5°E nominal	60.94	28.5	69.81	29.5
ETRS_1989_GK30FIN	3884	Finland - 29.5°E to 30.5°E nominal	61.43	29.5	67.98	30.5
ETRS_1989_GK31FIN	3885	Finland - east of 30.5°E nominal	62.08	30.5	64.27	31.59
ETRS_1989_Guernsey_Grid	3108	Channel Islands - Guernsey, Alderney, Sark	49.11	-3.73	50.16	-2.02
ETRS_1989_Jersey_Transverse_Mercator	3109	Channel Islands - Jersey, Les Ecrehos and Les Minquiers	48.77	-2.72	49.44	-1.81
ETRS_1989_Kosovo_Grid	102157	Serbia and Kosovo	41.85	18.81	46.19	23.01
ETRS_1989_Kp2000_Bornholm	2198	Denmark - onshore Bornholm	54.94	14.59	55.38	15.25
ETRS_1989_Kp2000_Jutland	2196	Denmark - onshore Jutland and Funen	54.67	8	57.8	11.29
ETRS_1989_Kp2000_Zealand	2197	Denmark - onshore Zealand and Lolland	54.51	10.79	56.79	12.69
ETRS_1989_LAEA	3035	Europe - ETRF by country	32.88	-16.1	84.73	40.18
ETRS_1989_LCC	3034	Europe - ETRF by country	32.88	-16.1	84.73	40.18
ETRS_1989_LCC_Germany_E-N	5243	Germany - onshore	47.27	5.86	55.09	15.04
ETRS_1989_LCC_Germany_N-E	4839	Germany - onshore	47.27	5.86	55.09	15.04
ETRS_1989_NTM_Zone_10	5110	Norway - onshore - 10°E to 11°E	58.9	10	65.04	11
ETRS_1989_NTM_Zone_11	5111	Norway - onshore - 11°E to 12°E	58.88	11	65.76	12
ETRS_1989_NTM_Zone_12	5112	Norway - onshore - 12°E to 13°E	59.88	12	68.15	13
ETRS_1989_NTM_Zone_13	5113	Norway - onshore - 13°E to 14°E	64.01	13	68.37	14
ETRS_1989_NTM_Zone_14	5114	Norway - onshore - 14°E to 15°E	64.03	14	69.05	15
ETRS_1989_NTM_Zone_15	5115	Norway - onshore - 15°E to 16°E	66.14	15	69.35	16
ETRS_1989_NTM_Zone_16	5116	Norway - onshore - 16°E to 17°E	66.88	16	69.45	17
ETRS_1989_NTM_Zone_17	5117	Norway - onshore - 17°E to 18°E	67.94	17	69.68	18
ETRS_1989_NTM_Zone_18	5118	Norway - onshore - 18°E to 19°E	68.04	18	70.27	19
ETRS_1989_NTM_Zone_19	5119	Norway - onshore - 19°E to 20°E	68.33	19	70.34	20
ETRS_1989_NTM_Zone_20	5120	Norway - onshore - 20°E to 21°E	68.37	20	70.29	21
ETRS_1989_NTM_Zone_21	5121	Norway - onshore - 21°E to 22°E	69.03	21	70.71	22
ETRS_1989_NTM_Zone_22	5122	Norway - onshore - 22°E to 23°E	68.69	22	70.81	23
ETRS_1989_NTM_Zone_23	5123	Norway - onshore - 23°E to 24°E	68.62	23	71.08	24
ETRS_1989_NTM_Zone_24	5124	Norway - onshore - 24°E to 25°E	68.58	24	71.16	25
ETRS_1989_NTM_Zone_25	5125	Norway - onshore - 25°E to 26°E	68.59	25	71.21	26
ETRS_1989_NTM_Zone_26	5126	Norway - onshore - 26°E to 27°E	69.71	26	71.17	27
ETRS_1989_NTM_Zone_27	5127	Norway - onshore - 27°E to 28°E	69.9	27	71.17	28
ETRS_1989_NTM_Zone_28	5128	Norway - onshore - 28°E to 29°E	69.03	28	71.13	29
ETRS_1989_NTM_Zone_29	5129	Norway - onshore - 29°E to 30°E	69.02	29	70.93	30
ETRS_1989_NTM_Zone_30	5130	Norway - onshore - east of 30°E	69.46	30	70.77	31.22
ETRS_1989_NTM_Zone_5	5105	Norway - onshore - west of 6°E	58.32	4.68	62.49	6
ETRS_1989_NTM_Zone_6	5106	Norway - onshore - 6°E to 7°E	57.93	6	63.02	7
ETRS_1989_NTM_Zone_7	5107	Norway - onshore - 7°E to 8°E	57.93	7	63.52	8
ETRS_1989_NTM_Zone_8	5108	Norway - onshore - 8°E to 9°E	58.03	8	63.87	9
ETRS_1989_NTM_Zone_9	5109	Norway - onshore - 9°E to 10°E	58.52	9	64.16	10
ETRS_1989_Poland_CS2000_Zone_5	2176	Poland - west of 16.5°E	50.26	14.14	55.35	16.5
ETRS_1989_Poland_CS2000_Zone_6	2177	Poland - 16.5°E to 19.5°E	49.39	16.5	55.93	19.5
ETRS_1989_Poland_CS2000_Zone_7	2178	Poland - 19.5°E to 22.5°E	49.09	19.5	54.55	22.5
ETRS_1989_Poland_CS2000_Zone_8	2179	Poland - east of 22.5°E	49	22.5	54.41	24.15
ETRS_1989_Poland_CS92	2180	Poland	49	14.14	55.93	24.15
ETRS_1989_Portugal_TM06	3763	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
ETRS_1989_Slovenia_TM	102109	Slovenia	45.42	13.38	46.88	16.61
ETRS_1989_TM_30_NE	2213	Romania - offshore	43.44	28.64	45.2	31.41
ETRS_1989_TM35FIN_NE	5048	Finland	58.84	19.08	70.09	31.59
ETRS_1989_TM_Baltic_1993	25884	Europe - Estonia; Latvia; Lithuania	53.89	19.02	60	28.24
ETRS_1989_UTM_Zone_26N	102097	Europe - 30°W to 24°W	25.1	-30	65.8	-24
ETRS_1989_UTM_Zone_27N	102098	Europe - 24°W to 18°W	27.6	-24	66.5	-18
ETRS_1989_UTM_Zone_28N	25828	Europe - 18°W to 12°W and ETRS89 by country	34.93	-16.1	72.44	-11.99
ETRS_1989_UTM_Zone_29N	25829	Europe - 12°W to 6°W and ETRS89 by country	34.91	-12	74.13	-6
ETRS_1989_UTM_Zone_30N	25830	Europe - 6°W to 0°W and ETRS89 by country	35.26	-6	80.49	0
ETRS_1989_UTM_Zone_31N	25831	Europe - 0°E to 6°E and ETRS89 by country	37	0	82.45	6.01
ETRS_1989_UTM_Zone_31N_N-zE	5651	Germany - west of 6°E	50.97	3.34	55.92	6
ETRS_1989_UTM_Zone_31N_zE-N	5649	Germany - west of 6°E	50.97	3.34	55.92	6
ETRS_1989_UTM_Zone_32N	25832	Europe - 6°E to 12°E and ETRS89 by country	38.76	6	84.33	12
ETRS_1989_UTM_Zone_32N_7stellen	102328	Germany - west of 12°E	47.27	5.5	55.9	12
ETRS_1989_UTM_Zone_32N_8stellen	102329	Germany - east of 12°E	47.27	12	55.9	15.03
ETRS_1989_UTM_Zone_32N_N-zE	5652	Germany - 6°E to 12°E	47.27	6	55.47	12
ETRS_1989_UTM_Zone_33N	25833	Europe - 12°E to 18°E and ETRS89 by country	46.4	12	84.42	18
ETRS_1989_UTM_Zone_33N_7stellen	102359	Germany - west of 12°E	47.27	5.5	55.9	12
ETRS_1989_UTM_Zone_33N_8stellen	102360	Germany - east of 12°E	47.27	12	55.9	15.03
ETRS_1989_UTM_Zone_33N_N-zE	5653	Germany - east of 12°E	47.46	11.57	55.03	15.04
ETRS_1989_UTM_Zone_33N_zE-N	5650	Germany - east of 12°E	47.46	11.57	55.03	15.04
ETRS_1989_UTM_Zone_34N	25834	Europe - 18°E to 24°E and ETRS89 by country	58.84	18	84.54	24.01
ETRS_1989_UTM_Zone_35N	25835	Europe - 24°E to 30°E and ETRS89 by country	59.64	24	84.73	30.01
ETRS_1989_UTM_Zone_36N	25836	Europe - 30°E to 36°E and ETRS89 by country	61.73	30	84.7	36.01
ETRS_1989_UTM_Zone_37N	25837	Europe - 36°E to 42°E and ETRS89 by country	72.99	36	79.07	38
ETRS_1989_UTM_Zone_38N	25838	Europe - 42°E to 48°E and ETRS89 by country	37	42	41.65	48
ETRS_1989_UTM_Zone_39N	102099	Europe - 48°E to 54°E	36	48	75	54
ETRS_1989_UTM_Zone_N32	4647	Germany - 6°E to 12°E	47.27	6	55.47	12
ETRS_1989_UWPP_1992	102173	Poland	49	14.14	55.93	24.15
ETRS_1989_UWPP_2000_PAS_5	102174	Poland - west of 16.5°E	50.26	14.14	55.35	16.5
ETRS_1989_UWPP_2000_PAS_6	102175	Poland - 16.5°E to 19.5°E	49.39	16.5	55.93	19.5
ETRS_1989_UWPP_2000_PAS_7	102176	Poland - 19.5°E to 22.5°E	49.09	19.5	54.55	22.5
ETRS_1989_UWPP_2000_PAS_8	102177	Poland - east of 22.5°E	49	22.5	54.41	24.15
EUREF_FIN_TM35FIN	3067	Finland	58.84	19.08	70.09	31.59
Europe_Albers_Equal_Area_Conic	102013	Europe	34	-30	85	50
Europe_Equidistant_Conic	102031	Europe	34	-30	85	50
Europe_Lambert_Conformal_Conic	102014	Europe	34	-30	85	50
Everest_Modified_1969_RSO_Malaya_ Meters	102061	Malaysia - West Malaysia - onshore	1.21	99.59	6.72	104.6
EWR2_Grid	9766	UK - Oxford to Bedford	51.7	-1.43	52.24	-0.36
Fahud_UTM_Zone_39N	23239	Oman - onshore west of 54°E	16.59	51.99	19.67	54
Fahud_UTM_Zone_40N	23240	Oman - mainland east of 54°E	16.89	54	26.42	59.91
Fatu_Iva_1972_UTM_Zone_7S	3303	French Polynesia - Marquesas Islands - Fatu Hiva	-10.6	-138.75	-10.36	-138.54
FD_1954_UTM_Zone_29N	3374	Faroe Islands - onshore	61.33	-7.49	62.41	-6.33
FD_1958_Iraq	3200	Iran - FD58	26.21	47.13	33.22	53.61
FEH2010_Fehmarnbelt_TM	5596	Europe - Fehmarnbelt outer	54.33	10.66	54.83	12.01
Fiji_1956_UTM_Zone_1S	3142	Fiji - main islands - east of 180°	-17.04	-180	-16.1	-179.77
Fiji_1956_UTM_Zone_60S	3141	Fiji - main islands - west of 180°	-19.22	176.81	-16.1	180
Fiji_1986_Fiji_Map_Grid	3460	Fiji - onshore	-20.81	176.81	-12.42	-178.15
Finland_Zone_1	2391	Finland - 19.5°E to 22.5°E onshore	59.76	19.5	69.33	22.5
Finland_Zone_2	2392	Finland - 22.5°E to 25.5°E onshore	59.75	22.5	68.9	25.5
Finland_Zone_3	2393	Finland - 25.5°E to 28.5°E onshore	60.18	25.5	70.09	28.51
Finland_Zone_4	2394	Finland - 28.5°E to 31.5°E	60.94	28.5	69.81	31.5
Fort_Desaix_UTM_20N	2973	Martinique - onshore	14.35	-61.29	14.93	-60.76
Fort_Marigot_UTM_20N	2969	Guadeloupe - St Martin and St Barthelemy - onshore	17.82	-63.21	18.17	-62.73
Garoua_UTM_Zone_33N	2312	Cameroon - Garoua area	8.92	12.9	9.87	14.19
GD_1949_New_Zealand_Map_Grid	27200	New Zealand - onshore	-47.33	166.37	-34.1	178.63
GDA_1994_Australia_Albers	3577	Australia - onshore	-43.7	112.85	-9.86	153.69
GDA_1994_BCSG02	3113	Australia - Brisbane	-29.88	151.19	-24.64	153.69
GDA_1994_CIG94	6721	Christmas Island - onshore	-10.63	105.48	-10.36	105.77
GDA_1994_CKIG94	6723	Cocos (Keeling) Islands - onshore	-12.27	96.76	-11.76	96.99
GDA_1994_Geoscience_Australia_ Lambert	3112	Australia - onshore	-43.7	112.85	-9.86	153.69
GDA_1994_MGA_zone_41	6732	Heard Island and McDonald Islands - west of 66°E	-57.5	62.92	-53.43	66
GDA_1994_MGA_zone_42	6733	Heard Island and McDonald Islands - 66°E to 72°E	-58.96	66	-51.18	72.01
GDA_1994_MGA_zone_43	6734	Heard Island and McDonald Islands - 72°E to 78°E	-59.02	72	-49.5	78.01
GDA_1994_MGA_zone_44	6735	Heard Island and McDonald Islands - east of 78°E	-58.47	78	-50.65	83.57
GDA_1994_MGA_Zone_46	6736	Cocos (Keeling) Islands - west of 96°E	-15.46	93.41	-8.57	96.01
GDA_1994_MGA_Zone_47	6737	Cocos (Keeling) Islands - east of 96°E	-15.56	96	-8.47	100.34
GDA_1994_MGA_Zone_48	28348	Australasia - Australia and Christmas Island - west of 108°E	-34.82	102.14	-8.72	108
GDA_1994_MGA_Zone_49	28349	Australasia - Australia and Christmas Island - 108°E to 114°E	-37.84	108	-10.72	114.01
GDA_1994_MGA_Zone_50	28350	Australia - 114°E to 120°E	-38.53	114	-12.06	120.01
GDA_1994_MGA_Zone_51	28351	Australia - 120°E to 126°E	-38.07	120	-10.46	126.01
GDA_1994_MGA_Zone_52	28352	Australia - 126°E to 132°E	-37.38	125.99	-9.1	132
GDA_1994_MGA_Zone_53	28353	Australia - 132°E to 138°E	-40.71	132	-8.88	138.01
GDA_1994_MGA_Zone_54	28354	Australia - 138°E to 144°E	-48.19	138	-9.08	144.01
GDA_1994_MGA_Zone_55	28355	Australia - 144°E to 150°E	-50.89	144	-9.23	150.01
GDA_1994_MGA_Zone_56	28356	Australia - 150°E to 156°E	-58.96	150	-13.87	156
GDA_1994_MGA_Zone_57	28357	Australia - 156°E to 162°E including Macquarie	-60.55	156	-14.08	162.01
GDA_1994_MGA_Zone_58	28358	Australasia - Australia and Norfolk Island - 162°E to 168°E	-59.39	162	-25.94	168
GDA_1994_MGA_Zone_59	6738	Norfolk Island - east of 168°E	-32.48	168	-25.61	173.35
GDA_1994_NSW_Lambert	3308	Australia - New South Wales	-37.53	140.99	-28.15	153.69
GDA2020_ALB2020	8013	Australia - Western Australia - Albany	-35.21	117.55	-34.75	118.22
GDA2020_BCG2020	8016	Australia - Western Australia - Busselton	-33.75	115.18	-33.4	115.87
GDA2020_BIO2020	8014	Australia - Western Australia - Barrow	-22.2	114.9	-20.21	115.59
GDA2020_BRO2020	8015	Australia - Western Australia - Broome	-18.09	122.08	-16.75	122.62
GDA2020_CARN2020	8017	Australia - Western Australia - Carnarvon	-25.5	113.33	-23	114
GDA2020_CIG2020	8018	Christmas Island - onshore	-10.63	105.48	-10.36	105.77
GDA2020_CKIG2020	8019	Cocos (Keeling) Islands - onshore	-12.27	96.76	-11.76	96.99
GDA2020_COL2020	8020	Australia - Western Australia - Collie	-34.67	115.73	-33.25	116.4
GDA2020_ESP2020	8021	Australia - Western Australia - Esperance	-34.5	121.56	-33.33	122.2
GDA2020_EXM2020	8022	Australia - Western Australia - Exmouth	-22.42	113.75	-21.75	114.25
GDA2020_GA_LCC	7845	Australia - onshore	-43.7	112.85	-9.86	153.69
GDA2020_GCG2020	8023	Australia - Western Australia - Geraldton	-29.1	114.51	-28.48	115
GDA2020_GOLD2020	8024	Australia - Western Australia - Kalgoorlie	-32.25	121	-28.75	121.84
GDA2020_JCG2020	8025	Australia - Western Australia - Jurien Bay	-30.74	114.83	-29.08	115.34
GDA2020_KALB2020	8026	Australia - Western Australia - Kalbarri	-28.5	113.9	-27.16	114.75
GDA2020_KAR2020	8027	Australia - Western Australia - Karratha	-20.92	116.58	-20.25	117.25
GDA2020_KUN2020	8028	Australia - Western Australia - Kununurra	-16.75	128.5	-14.75	129
GDA2020_LCG2020	8029	Australia - Western Australia - Lancelin	-31.49	115.15	-30.71	115.62
GDA2020_MGA_Zone_46	7846	Cocos (Keeling) Islands - west of 96°E	-15.46	93.41	-8.57	96.01
GDA2020_MGA_Zone_47	7847	Cocos (Keeling) Islands - east of 96°E	-15.56	96	-8.47	100.34
GDA2020_MGA_Zone_48	7848	Australasia - Australia and Christmas Island - west of 108°E	-34.68	102.14	-8.87	108.01
GDA2020_MGA_Zone_49	7849	Australasia - Australia and Christmas Island - 108°E to 114°E	-37.84	108	-10.72	114.01
GDA2020_MGA_Zone_50	7850	Australia - 114°E to 120°E	-38.53	114	-12.06	120.01
GDA2020_MGA_Zone_51	7851	Australia - 120°E to 126°E	-38.07	120	-10.46	126.01
GDA2020_MGA_Zone_52	7852	Australia - 126°E to 132°E	-37.38	125.99	-9.1	132
GDA2020_MGA_Zone_53	7853	Australia - 132°E to 138°E	-40.71	132	-8.88	138.01
GDA2020_MGA_Zone_54	7854	Australia - 138°E to 144°E	-48.19	138	-9.08	144.01
GDA2020_MGA_Zone_55	7855	Australia - 144°E to 150°E	-50.89	144	-9.23	150
GDA2020_MGA_Zone_56	7856	Australia - 150°E to 156°E	-58.96	150	-13.87	156
GDA2020_MGA_Zone_57	7857	Australia - 156°E to 162°E including Macquarie	-60.56	156	-14.08	162.01
GDA2020_MGA_Zone_58	7858	Australasia - Australia and Norfolk Island - 162°E to 168°E	-59.39	162	-25.94	168
GDA2020_MGA_Zone_59	7859	Norfolk Island - east of 168°E	-32.48	168	-25.61	173.35
GDA2020_MRCG2020	8030	Australia - Western Australia - Margaret River	-34.42	114.96	-33.51	115.24
GDA2020_NSW_Lambert	8058	Australia - New South Wales	-37.53	140.99	-28.15	153.69
GDA2020_PCG2020	8031	Australia - Western Australia - Perth	-33.42	115.44	-31.33	116.09
GDA_1994_Perth_Coastal_Grid_1994	102216	Australia - Perth Coast	-33.417	115.442	-31.333	116.083
GDA_1994_WEIPA	8391	Australia - Queensland - Weipa	-13.5	141.5	-11.49	142.51
GDA2020_PHG2020	8032	Australia - Western Australia - Port Hedland	-20.79	118.25	-20.1	118.97
GDA_1994_South_Australia_Lambert	3107	Australia - SA	-38.13	128.99	-25.99	141.01
GDA2020_Vicgrid	7899	Australia - Victoria	-39.2	140.96	-33.98	150.04
GDA_1994_VICGRID94	3111	Australia - Victoria	-39.2	140.96	-33.98	150.04
GDBD2009_GEORSO	5247	Brunei	4.01	112.37	6.31	115.37
GDM_2000_BRSO_East_Malaysia	3376	Malaysia - East Malaysia	0.85	109.31	7.67	119.61
GDM_2000_MRSO_Peninsular_Malaysia	3375	Malaysia - West Malaysia	1.13	98.02	7.81	105.82
GDM_2000_State_Cassini_Johor	3377	Malaysia - West Malaysia - Johor	1.21	102.44	2.95	104.6
GDM_2000_State_Cassini_Kelantan	3385	Malaysia - West Malaysia - Kelantan	4.54	101.33	6.29	102.67
GDM_2000_State_Cassini_Negeri_ Sembilan_and_Melaka	3378	Malaysia - West Malaysia - Sembilan and Melaka	2.03	101.7	3.28	102.71
GDM_2000_State_Cassini_Pahang	3379	Malaysia - West Malaysia - Pahang	2.45	101.33	4.78	103.67
GDM_2000_State_Cassini_Perak	3384	Malaysia - West Malaysia - Perak	3.66	100.07	5.92	102
GDM_2000_State_Cassini_Perlis	3383	Malaysia - West Malaysia - Kedah and Perlis	5.08	99.59	6.72	101.12
GDM_2000_State_Cassini_Pulau_Pinang_ and_Seberang_Perai	3382	Malaysia - West Malaysia - Pulau Pinang	5.12	100.12	5.59	100.56
GDM_2000_State_Cassini_Selangor	3380	Malaysia - West Malaysia - Selangor	2.54	100.76	3.87	101.97
GDM_2000_State_Cassini_Terengganu	3381	Malaysia - West Malaysia - Terengganu	3.89	102.38	5.9	103.72
GDM2008_LGM2012	103872	Mauritius	-23.81	53.8	-8.43	67.05
Germany_Zone_1	31491	Germany - offshore North Sea west of 4.5°E	55.24	3.34	55.92	4.5
Germany_Zone_2	31492	Germany - West Germany - west of 7.5°E	49.11	5.86	53.81	7.5
Germany_Zone_3	31493	Germany - West- Germany - 7.5°E to 10.5°E	47.27	7.5	55.09	10.51
Germany_Zone_4	31494	Germany - West Germany - 10.5°E to 13.5°E	47.39	10.5	54.59	13.51
Germany_Zone_5	31495	Germany - West Germany - east of 13.5°E	48.51	13.5	48.98	13.84
Ghana_Metre_Grid	25000	Ghana	1.4	-3.79	11.16	2.1
GOES-16_East_ABI_Fixed_Grid_ITRF2008	102498	GOES-16 East Full disk	-81.3282	-156.2995	81.3282	6.2995
GR96_EPSG_Arctic_zone_1-25	6050	Arctic - 87°50'N to 82°50'N, 60°W to 0°E	82.83	-60	87.84	0
GR96_EPSG_Arctic_zone_2-18	6051	Arctic - 84°30'N to 79°30'N, 72°W to 32°W	79.5	-72	84.51	-32
GR96_EPSG_Arctic_zone_2-20	6052	Arctic - 84°30'N to 79°30'N, 32°W to 8°E	79.5	-32	84.51	8.01
GR96_EPSG_Arctic_zone_3-29	6053	Arctic - 81°10'N to 76°10'N, Greenland west of 54°W	76.16	-75	81.17	-54
GR96_EPSG_Arctic_zone_3-31	6054	Arctic - 81°10'N to 76°10'N, 54°W to 24°W	76.16	-54	81.17	-24
GR96_EPSG_Arctic_zone_3-33	6055	Arctic - 81°10'N to 76°10'N, 24°W to 3°E	76.16	-24	81.17	1.89
GR96_EPSG_Arctic_zone_4-20	6056	Arctic - 77°50'N to 72°50'N, 76°W to 51°W	72.83	-76	77.84	-51
GR96_EPSG_Arctic_zone_4-22	6057	Arctic - 77°50'N to 72°50'N, 51°W to 26°W	72.83	-51	77.84	-26
GR96_EPSG_Arctic_zone_4-24	6058	Arctic - 77°50'N to 72°50'N, 26°W to 2°W	72.83	-26	77.84	-2
GR96_EPSG_Arctic_zone_5-41	6059	Arctic - 74°30'N to 69°30'N, 72°W to 52°W	69.48	-71.89	74.51	-51.99
GR96_EPSG_Arctic_zone_5-43	6060	Arctic - 74°30'N to 69°30'N, 52°W to 32°W	69.5	-52	74.51	-32
GR96_EPSG_Arctic_zone_5-45	6061	Arctic - 74°30'N to 69°30'N, 32°W to 12°W	69.5	-32	74.51	-12
GR96_EPSG_Arctic_zone_6-26	6062	Arctic - 71°10'N to 66°10'N, 65°W to 47°W	66.16	-65	71.17	-47
GR96_EPSG_Arctic_zone_6-28	6063	Arctic - 71°10'N to 66°10'N, 47°W to 29°W	66.16	-47	71.17	-29
GR96_EPSG_Arctic_zone_6-30	6064	Arctic - 71°10'N to 66°10'N, 29°W to 11°W	66.16	-29	71.17	-11
GR96_EPSG_Arctic_zone_7-11	6065	Arctic - 67°50'N to 62°50'N, 59°W to 42°W	62.83	-59	67.84	-42
GR96_EPSG_Arctic_zone_7-13	6066	Arctic - 67°50'N to 62°50'N, 42°W to 25°W	62.83	-42	67.84	-25
GR96_EPSG_Arctic_zone_8-20	6067	Arctic - 64°30'N to 59°30'N, 59°W to 44°W	59.5	-59	64.51	-44
GR96_EPSG_Arctic_zone_8-22	6068	Arctic - 64°30'N to 59°30'N, 44°W to 29°W	59.5	-44	64.51	-29
Graciosa_Base_SW_1948_UTM_Zone_ 26N	102162	Portugal - Azores C - onshore	38.32	-28.9	39.14	-26.97
Grand_Cayman_1959_UTM_Zone_17N	3356	Cayman Islands - Grand Cayman	19.21	-81.46	19.41	-81.04
Grand_Cayman_National_Grid_1959	6128	Cayman Islands - Grand Cayman	19.21	-81.46	19.41	-81.04
Grand_Comoros_UTM_38S	2999	Comoros - Njazidja (Grande Comore)	-11.99	43.16	-11.31	43.55
Greek_Grid	2100	Greece - onshore	34.88	19.57	41.75	28.3
Greenland_1996_UTM_Zone_18N	3178	Greenland - west of 72°W	74.52	-75	79.04	-72
Greenland_1996_UTM_Zone_19N	3179	Greenland - 72°W to 66°W	73.24	-72	80.9	-66
Greenland_1996_UTM_Zone_20N	3180	Greenland - 66°W to 60°W	68.92	-66	82.22	-60
Greenland_1996_UTM_Zone_21N	3181	Greenland - 60°W to 54°W	58.91	-60	84	-54
Greenland_1996_UTM_Zone_22N	3182	Greenland - 54°W to 48°W	56.9	-54	84	-48
Greenland_1996_UTM_Zone_23N	3183	Greenland - 48°W to 42°W	56.38	-48	84	-42
Greenland_1996_UTM_Zone_24N	3184	Greenland - 42°W to 36°W	56.56	-42	84	-36
Greenland_1996_UTM_Zone_25N	3185	Greenland - 36°W to 30°W	60.16	-36	84	-30
Greenland_1996_UTM_Zone_26N	3186	Greenland - 30°W to 24°W	64.96	-30	84	-24
Greenland_1996_UTM_Zone_27N	3187	Greenland - 24°W to 18°W	67.7	-24	84	-18
Greenland_1996_UTM_Zone_28N	3188	Greenland - 18°W to 12°W	68.67	-18	84	-12
Greenland_1996_UTM_Zone_29N	3189	Greenland - 12°W to 6°W	72.43	-12	84	-6
Grenada_1953_British_West_Indies_Grid	2003	Grenada and southern Grenadines - onshore	11.94	-61.84	12.57	-61.35
GSK-2011_Gauss-Kruger_CM_105E	21018	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
GSK-2011_Gauss-Kruger_CM_111E	21019	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
GSK-2011_Gauss-Kruger_CM_117E	21020	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
GSK-2011_Gauss-Kruger_CM_123E	21021	Russia - 120°E to 126°E onshore	51.51	120	74	126
GSK-2011_Gauss-Kruger_CM_129E	21022	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
GSK-2011_Gauss-Kruger_CM_135E	21023	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
GSK-2011_Gauss-Kruger_CM_141E	21024	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
GSK-2011_Gauss-Kruger_CM_147E	21025	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
GSK-2011_Gauss-Kruger_CM_153E	21026	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
GSK-2011_Gauss-Kruger_CM_159E	21027	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
GSK-2011_Gauss-Kruger_CM_165E	21028	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
GSK-2011_Gauss-Kruger_CM_171E	21029	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
GSK-2011_Gauss-Kruger_CM_171W	21032	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
GSK-2011_Gauss-Kruger_CM_177E	21030	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
GSK-2011_Gauss-Kruger_CM_177W	21031	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
GSK-2011_Gauss-Kruger_CM_21E	21004	Russia - west of 24°E onshore	54.32	19.57	55.32	22.87
GSK-2011_Gauss-Kruger_CM_27E	21005	Russia - 24°E to 30°E onshore	55.69	26.61	69.47	30
GSK-2011_Gauss-Kruger_CM_33E	21006	Russia - 30°E to 36°E onshore	50.34	30	70.02	36
GSK-2011_Gauss-Kruger_CM_39E	21007	Russia - 36°E to 42°E onshore	43.18	36	69.23	42.01
GSK-2011_Gauss-Kruger_CM_45E	21008	Russia - 42°E to 48°E onshore	41.19	42	80.91	48
GSK-2011_Gauss-Kruger_CM_51E	21009	Russia - 48°E to 54°E onshore	41.39	48	81.4	54
GSK-2011_Gauss-Kruger_CM_57E	21010	Russia - 54°E to 60°E onshore	50.47	54	81.91	60
GSK-2011_Gauss-Kruger_CM_63E	21011	Russia - 60°E to 66°E onshore	50.66	60	81.77	66
GSK-2011_Gauss-Kruger_CM_69E	21012	Russia - 66°E to 72°E onshore	54.1	66	77.07	72
GSK-2011_Gauss-Kruger_CM_75E	21013	Russia - 72°E to 78°E onshore	53.17	72	79.71	78
GSK-2011_Gauss-Kruger_CM_81E	21014	Russia - 78°E to 84°E onshore	50.69	78	81.03	84
GSK-2011_Gauss-Kruger_CM_87E	21015	Russia - 84°E to 90°E onshore	49.07	84	81.27	90
GSK-2011_Gauss-Kruger_CM_93E	21016	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
GSK-2011_Gauss-Kruger_CM_99E	21017	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
GSK-2011_Gauss-Kruger_zone_10	20910	Russia - 54°E to 60°E onshore	50.47	54	81.91	60
GSK-2011_Gauss-Kruger_zone_11	20911	Russia - 60°E to 66°E onshore	50.66	60	81.77	66
GSK-2011_Gauss-Kruger_zone_12	20912	Russia - 66°E to 72°E onshore	54.1	66	77.07	72
GSK-2011_Gauss-Kruger_zone_13	20913	Russia - 72°E to 78°E onshore	53.17	72	79.71	78
GSK-2011_Gauss-Kruger_zone_14	20914	Russia - 78°E to 84°E onshore	50.69	78	81.03	84
GSK-2011_Gauss-Kruger_zone_15	20915	Russia - 84°E to 90°E onshore	49.07	84	81.27	90
GSK-2011_Gauss-Kruger_zone_16	20916	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
GSK-2011_Gauss-Kruger_zone_17	20917	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
GSK-2011_Gauss-Kruger_zone_18	20918	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
GSK-2011_Gauss-Kruger_zone_19	20919	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
GSK-2011_Gauss-Kruger_zone_20	20920	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
GSK-2011_Gauss-Kruger_zone_21	20921	Russia - 120°E to 126°E onshore	51.51	120	74	126
GSK-2011_Gauss-Kruger_zone_22	20922	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
GSK-2011_Gauss-Kruger_zone_23	20923	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
GSK-2011_Gauss-Kruger_zone_24	20924	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
GSK-2011_Gauss-Kruger_zone_25	20925	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
GSK-2011_Gauss-Kruger_zone_26	20926	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
GSK-2011_Gauss-Kruger_zone_27	20927	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
GSK-2011_Gauss-Kruger_zone_28	20928	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
GSK-2011_Gauss-Kruger_zone_29	20929	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
GSK-2011_Gauss-Kruger_zone_30	20930	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
GSK-2011_Gauss-Kruger_zone_31	20931	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
GSK-2011_Gauss-Kruger_zone_32	20932	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
GSK-2011_Gauss-Kruger_zone_4	20904	Russia - west of 24°E onshore	54.32	19.57	55.32	22.87
GSK-2011_Gauss-Kruger_zone_5	20905	Russia - 24°E to 30°E onshore	55.69	26.61	69.47	30
GSK-2011_Gauss-Kruger_zone_6	20906	Russia - 30°E to 36°E onshore	50.34	30	70.02	36
GSK-2011_Gauss-Kruger_zone_7	20907	Russia - 36°E to 42°E onshore	43.18	36	69.23	42.01
GSK-2011_Gauss-Kruger_zone_8	20908	Russia - 42°E to 48°E onshore	41.19	42	80.91	48
GSK-2011_Gauss-Kruger_zone_9	20909	Russia - 48°E to 54°E onshore	41.39	48	81.4	54
GSK-2011_GSK_3GK_CM_102E	21334	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
GSK-2011_GSK_3GK_CM_105E	21335	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
GSK-2011_GSK_3GK_CM_108E	21336	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
GSK-2011_GSK_3GK_CM_111E	21337	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
GSK-2011_GSK_3GK_CM_114E	21338	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
GSK-2011_GSK_3GK_CM_117E	21339	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
GSK-2011_GSK_3GK_CM_120E	21340	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
GSK-2011_GSK_3GK_CM_123E	21341	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
GSK-2011_GSK_3GK_CM_126E	21342	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
GSK-2011_GSK_3GK_CM_129E	21343	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
GSK-2011_GSK_3GK_CM_132E	21344	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
GSK-2011_GSK_3GK_CM_135E	21345	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
GSK-2011_GSK_3GK_CM_138E	21346	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
GSK-2011_GSK_3GK_CM_141E	21347	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
GSK-2011_GSK_3GK_CM_144E	21348	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
GSK-2011_GSK_3GK_CM_147E	21349	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
GSK-2011_GSK_3GK_CM_150E	21350	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
GSK-2011_GSK_3GK_CM_153E	21351	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
GSK-2011_GSK_3GK_CM_156E	21352	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
GSK-2011_GSK_3GK_CM_159E	21353	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
GSK-2011_GSK_3GK_CM_162E	21354	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
GSK-2011_GSK_3GK_CM_165E	21355	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
GSK-2011_GSK_3GK_CM_168E	21356	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
GSK-2011_GSK_3GK_CM_168W	21364	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
GSK-2011_GSK_3GK_CM_171E	21357	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
GSK-2011_GSK_3GK_CM_171W	21363	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
GSK-2011_GSK_3GK_CM_174E	21358	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
GSK-2011_GSK_3GK_CM_174W	21362	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
GSK-2011_GSK_3GK_CM_177E	21359	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
GSK-2011_GSK_3GK_CM_177W	21361	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
GSK-2011_GSK_3GK_CM_180E	21360	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
GSK-2011_GSK_3GK_CM_21E	21307	Russia - 19.5°E to 22.5°E onshore	54.32	19.57	55.32	22.5
GSK-2011_GSK_3GK_CM_24E	21308	Russia - 22.5°E to 25.5°E onshore	54.34	22.5	55.07	22.87
GSK-2011_GSK_3GK_CM_27E	21309	Russia - 25.5°E to 28.5°E onshore	56.05	26.61	68.93	28.51
GSK-2011_GSK_3GK_CM_30E	21310	Russia - 28.5°E to 31.5°E onshore	52.85	28.5	69.85	31.5
GSK-2011_GSK_3GK_CM_33E	21311	Russia - 31.5°E to 34.5°E onshore	51.24	31.5	70.02	34.5
GSK-2011_GSK_3GK_CM_36E	21312	Russia - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.51
GSK-2011_GSK_3GK_CM_39E	21313	Russia - 37.5°E to 40.5°E onshore	43.33	37.5	68.8	40.5
GSK-2011_GSK_3GK_CM_42E	21314	Russia - 40.5°E to 43.5°E onshore	42.87	40.5	68.74	43.5
GSK-2011_GSK_3GK_CM_45E	21315	Russia - 43.5°E to 46.5°E onshore	41.89	43.5	80.8	46.5
GSK-2011_GSK_3GK_CM_48E	21316	Russia - 46.5°E to 49.5°E onshore	41.19	46.5	80.91	49.5
GSK-2011_GSK_3GK_CM_51E	21317	Russia - 49.5°E to 52.5°E onshore	42.36	49.5	81.22	52.5
GSK-2011_GSK_3GK_CM_54E	21318	Russia - 52.5°E to 55.5°E onshore	50.52	52.5	81.41	55.5
GSK-2011_GSK_3GK_CM_57E	21319	Russia - 55.5°E to 58.5°E onshore	50.53	55.5	81.89	58.5
GSK-2011_GSK_3GK_CM_60E	21320	Russia - 58.5°E to 61.5°E onshore	50.47	58.5	81.91	61.5
GSK-2011_GSK_3GK_CM_63E	21321	Russia - 61.5°E to 64.5°E onshore	51.03	61.5	81.77	64.5
GSK-2011_GSK_3GK_CM_66E	21322	Russia - 64.5°E to 67.5°E onshore	54.31	64.5	81.25	67.5
GSK-2011_GSK_3GK_CM_69E	21323	Russia - 67.5°E to 70.5°E onshore	54.85	67.5	77.07	70.5
GSK-2011_GSK_3GK_CM_72E	21324	Russia - 70.5°E to 73.5°E onshore	53.43	70.5	73.57	73.5
GSK-2011_GSK_3GK_CM_75E	21325	Russia - 73.5°E to 76.5°E onshore	53.47	73.5	79.71	76.5
GSK-2011_GSK_3GK_CM_78E	21326	Russia - 76.5°E to 79.5°E onshore	51.49	76.5	81.03	79.5
GSK-2011_GSK_3GK_CM_81E	21327	Russia - 79.5°E to 82.5°E onshore	50.7	79.5	81.03	82.5
GSK-2011_GSK_3GK_CM_84E	21328	Russia - 82.5°E to 85.5°E onshore	49.58	82.5	77.56	85.5
GSK-2011_GSK_3GK_CM_87E	21329	Russia - 85.5°E to 88.5°E onshore	49.07	85.5	77.16	88.5
GSK-2011_GSK_3GK_CM_90E	21330	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
GSK-2011_GSK_3GK_CM_93E	21331	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
GSK-2011_GSK_3GK_CM_96E	21332	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
GSK-2011_GSK_3GK_CM_99E	21333	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
GSK-2011_GSK_3GK_zone_10	21210	Russia - 28.5°E to 31.5°E onshore	52.85	28.5	69.85	31.5
GSK-2011_GSK_3GK_zone_11	21211	Russia - 31.5°E to 34.5°E onshore	51.24	31.5	70.02	34.5
GSK-2011_GSK_3GK_zone_12	21212	Russia - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.51
GSK-2011_GSK_3GK_zone_13	21213	Russia - 37.5°E to 40.5°E onshore	43.33	37.5	68.8	40.5
GSK-2011_GSK_3GK_zone_14	21214	Russia - 40.5°E to 43.5°E onshore	42.87	40.5	68.74	43.5
GSK-2011_GSK_3GK_zone_15	21215	Russia - 43.5°E to 46.5°E onshore	41.89	43.5	80.8	46.5
GSK-2011_GSK_3GK_zone_16	21216	Russia - 46.5°E to 49.5°E onshore	41.19	46.5	80.91	49.5
GSK-2011_GSK_3GK_zone_17	21217	Russia - 49.5°E to 52.5°E onshore	42.36	49.5	81.22	52.5
GSK-2011_GSK_3GK_zone_18	21218	Russia - 52.5°E to 55.5°E onshore	50.52	52.5	81.41	55.5
GSK-2011_GSK_3GK_zone_19	21219	Russia - 55.5°E to 58.5°E onshore	50.53	55.5	81.89	58.5
GSK-2011_GSK_3GK_zone_20	21220	Russia - 58.5°E to 61.5°E onshore	50.47	58.5	81.91	61.5
GSK-2011_GSK_3GK_zone_21	21221	Russia - 61.5°E to 64.5°E onshore	51.03	61.5	81.77	64.5
GSK-2011_GSK_3GK_zone_22	21222	Russia - 64.5°E to 67.5°E onshore	54.31	64.5	81.25	67.5
GSK-2011_GSK_3GK_zone_23	21223	Russia - 67.5°E to 70.5°E onshore	54.85	67.5	77.07	70.5
GSK-2011_GSK_3GK_zone_24	21224	Russia - 70.5°E to 73.5°E onshore	53.43	70.5	73.57	73.5
GSK-2011_GSK_3GK_zone_25	21225	Russia - 73.5°E to 76.5°E onshore	53.47	73.5	79.71	76.5
GSK-2011_GSK_3GK_zone_26	21226	Russia - 76.5°E to 79.5°E onshore	51.49	76.5	81.03	79.5
GSK-2011_GSK_3GK_zone_27	21227	Russia - 79.5°E to 82.5°E onshore	50.7	79.5	81.03	82.5
GSK-2011_GSK_3GK_zone_28	21228	Russia - 82.5°E to 85.5°E onshore	49.58	82.5	77.56	85.5
GSK-2011_GSK_3GK_zone_29	21229	Russia - 85.5°E to 88.5°E onshore	49.07	85.5	77.16	88.5
GSK-2011_GSK_3GK_zone_30	21230	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
GSK-2011_GSK_3GK_zone_31	21231	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
GSK-2011_GSK_3GK_zone_32	21232	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
GSK-2011_GSK_3GK_zone_33	21233	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
GSK-2011_GSK_3GK_zone_34	21234	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
GSK-2011_GSK_3GK_zone_35	21235	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
GSK-2011_GSK_3GK_zone_36	21236	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
GSK-2011_GSK_3GK_zone_37	21237	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
GSK-2011_GSK_3GK_zone_38	21238	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
GSK-2011_GSK_3GK_zone_39	21239	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
GSK-2011_GSK_3GK_zone_40	21240	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
GSK-2011_GSK_3GK_zone_41	21241	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
GSK-2011_GSK_3GK_zone_42	21242	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
GSK-2011_GSK_3GK_zone_43	21243	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
GSK-2011_GSK_3GK_zone_44	21244	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
GSK-2011_GSK_3GK_zone_45	21245	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
GSK-2011_GSK_3GK_zone_46	21246	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
GSK-2011_GSK_3GK_zone_47	21247	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
GSK-2011_GSK_3GK_zone_48	21248	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
GSK-2011_GSK_3GK_zone_49	21249	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
GSK-2011_GSK_3GK_zone_50	21250	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
GSK-2011_GSK_3GK_zone_51	21251	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
GSK-2011_GSK_3GK_zone_52	21252	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
GSK-2011_GSK_3GK_zone_53	21253	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
GSK-2011_GSK_3GK_zone_54	21254	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
GSK-2011_GSK_3GK_zone_55	21255	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
GSK-2011_GSK_3GK_zone_56	21256	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
GSK-2011_GSK_3GK_zone_57	21257	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
GSK-2011_GSK_3GK_zone_58	21258	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
GSK-2011_GSK_3GK_zone_59	21259	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
GSK-2011_GSK_3GK_zone_60	21260	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
GSK-2011_GSK_3GK_zone_61	21261	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
GSK-2011_GSK_3GK_zone_62	21262	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
GSK-2011_GSK_3GK_zone_63	21263	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
GSK-2011_GSK_3GK_zone_64	21264	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
GSK-2011_GSK_3GK_zone_7	21207	Russia - 19.5°E to 22.5°E onshore	54.32	19.57	55.32	22.5
GSK-2011_GSK_3GK_zone_8	21208	Russia - 22.5°E to 25.5°E onshore	54.34	22.5	55.07	22.87
GSK-2011_GSK_3GK_zone_9	21209	Russia - 25.5°E to 28.5°E onshore	56.05	26.61	68.93	28.51
GTM	103598	Guatemala	10.6	-94.57	17.83	-88.16
Guam_1963_Yap_Islands	3295	Micronesia - Yap Islands	9.39	137.99	9.69	138.27
Guam_Geodetic_Network_1993	102240	Guam	10.95	141.19	15.91	148.18
Guam_Geodetic_Triangulation_Network_ 1963	102239	Guam	10.95	141.19	15.91	148.18
Guernsey_Grid	102070	Channel Islands - Guernsey, Alderney, Sark	49.11	-3.73	50.16	-2.02
Gulshan_303_Bangladesh_TM	3106	Bangladesh	18.56	88.01	26.64	92.67
Gunung_Segara_Jakarta_NEIEZ	5329	Indonesia - Kalimantan E	-4.24	114.55	4.29	119.06
Gunung_Segara_NEIEZ	3000	Indonesia - Kalimantan E	-4.24	114.55	4.29	119.06
Gunung_Segara_UTM_Zone_50S	2933	Indonesia - Kalimantan - Mahakam delta	-1.24	116.72	0	117.99
Hanoi_1972_GK_106_NE	2093	Vietnam - onshore Vung Tau area	9.03	105.49	11.04	107.58
Hanoi_1972_GK_Zone_18	2044	Vietnam - west of 108°E onshore	8.33	102.14	23.4	108
Hanoi_1972_GK_Zone_19	2045	Vietnam - east of 108°E onshore	10.43	108	21.56	109.53
Hartebeesthoek94_Lo15	102480	Namibia - Walvis Bay	-23.15	14.35	-22.68	14.6
Hartebeesthoek94_Lo17	102481	South Africa - west of 18°E	-33.1	16.45	-28.03	18
Hartebeesthoek94_Lo19	102482	South Africa - 18°E to 20°E	-34.88	17.99	-28.38	20
Hartebeesthoek94_Lo21	102483	South Africa - 20°E to 22°E	-34.88	19.99	-24.76	22.01
Hartebeesthoek94_Lo23	102484	South Africa - 22°E to 24°E	-34.26	22	-25.26	24.01
Hartebeesthoek94_Lo25	102485	South Africa - 24°E to 26°E	-34.26	24	-24.71	26.01
Hartebeesthoek94_Lo27	102486	South Africa - 26°E to 28°E	-33.83	26	-22.92	28
Hartebeesthoek94_Lo29	102487	South Africa - 28°E to 30°E	-33.03	27.99	-22.13	30
Hartebeesthoek94_Lo31	102488	South Africa - 30°E to 32°E	-31.38	29.99	-22.22	32.02
Hartebeesthoek94_Lo33	102489	South Africa - east of 32°E	-28.94	31.95	-26.8	32.95
Hartebeesthoek94_Lo19_(E-N)	102562	South Africa - 18°E to 20°E	-34.88	17.99	-28.38	20
Hartebeesthoek94_Lo21_(E-N)	102563	South Africa - 20°E to 22°E	-34.88	19.99	-24.76	22.01
Hartebeesthoek94_Lo23_(E-N)	102564	South Africa - 22°E to 24°E	-34.26	22	-25.26	24.01
Hartebeesthoek94_Lo25_(E-N)	102565	South Africa - 24°E to 26°E	-34.26	24	-24.71	26.01
Hartebeesthoek94_Lo27_(E-N)	102566	South Africa - 26°E to 28°E	-33.83	26	-22.92	28
Hartebeesthoek94_Lo29_(E-N)	102567	South Africa - 28°E to 30°E	-33.03	27.99	-22.13	30
Hartebeesthoek94_Lo31_(E-N)	102568	South Africa - 30°E to 32°E	-31.38	29.99	-22.22	32.02
Hartebeesthoek94_ZAF_BSU_Albers_25E	9221	South Africa - mainland - onshore and offshore	-38.17	13.33	-22.13	36.54
Hartebeesthoek94_ZAF_BSU_Albers_44E	9222	South Africa - Prince Edward islands - onshore and offshore	-50.32	32.71	-43.26	42.85
Hawaii_Albers_Equal_Area_Conic	102007	USA - Hawaii - onshore	18.87	-160.3	22.29	-154.74
Helle_1954_Jan_Mayen_Grid	3058	Jan Mayen - onshore	70.75	-9.17	71.24	-7.87
Hito_XVIII_1963_Argentina_2	2083	Argentina - Tierra del Fuego onshore west of 67.5°W	-54.9	-68.64	-52.59	-67.5
Hito_XVIII_1963_UTM_19S	2084	Argentina - Tierra del Fuego offshore west of 66°W	-54.61	-68.62	-51.65	-66
HJAIA_AirportGrid_2Mar10	102460	HJAIA - Hartsfield- Jackson Atlanta Intl Airport	33.591	-84.502	33.684	-84.351
Hjorsey_1955_UTM_Zone_26N	3054	Iceland - onshore west of 24°W	64.71	-24.66	65.86	-24
Hjorsey_1955_UTM_Zone_27N	3055	Iceland - onshore 24°W to 18°W	63.34	-24	66.52	-18
Hjorsey_1955_UTM_Zone_28N	3056	Iceland - onshore east of 18°W	63.45	-18	66.59	-13.38
Hong_Kong_1963_Grid_System	3407	China - Hong Kong	22.13	113.76	22.58	114.51
Hong_Kong_1980_Grid	2326	China - Hong Kong	22.13	113.76	22.58	114.51
Hong_Kong_1980_UTM_Zone_49N	102141	China - Hong Kong	22.13	113.76	22.58	114.51
Hong_Kong_1980_UTM_Zone_50N	102142	China - Hong Kong	22.13	113.76	22.58	114.51
HTRS96_Croatia_LCC	3766	Croatia	41.62	13	46.54	19.43
HTRS96_Croatia_TM	3765	Croatia - onshore	42.34	13.43	46.54	19.43
HTRS96_UTM_Zone_33N	3767	Croatia - west of 18°E	41.63	13	46.54	18
HTRS96_UTM_Zone_34N	3768	Croatia - east of 18°E	41.62	18	45.92	19.43
Hungarian_1972_Egyseges_Orszagos_ Vetuleti	23700	Hungary	45.74	16.11	48.58	22.9
Hu_Tzu_Shan_UTM_Zone_51N	3829	Taiwan - onshore - mainland and Penghu	21.87	119.25	25.34	122.06
IGC_1962_Congo_TM_Zone_12	3318	Congo DR (Zaire) - 11°E to 13°E onshore	-6.04	12.17	-4.67	13.01
IGC_1962_Congo_TM_Zone_14	3319	Congo DR (Zaire) - 13°E to 15°E	-5.91	13	-4.28	15.01
IGC_1962_Congo_TM_Zone_16	3320	Congo DR (Zaire) - 6th parallel south 15°E to 17°E	-5.87	15	-3.29	17
IGC_1962_Congo_TM_Zone_18	3321	Congo DR (Zaire) - 6th parallel south 17°E to 19°E	-5.38	17	-3.4	19
IGC_1962_Congo_TM_Zone_20	3322	Congo DR (Zaire) - 6th parallel south 19°E to 21°E	-7.29	19	-4.01	21
IGC_1962_Congo_TM_Zone_22	3323	Congo DR (Zaire) - 6th parallel south 21°E to 23°E	-7.31	21	-5.31	23
IGC_1962_Congo_TM_Zone_24	3324	Congo DR (Zaire) - 6th parallel south 23°E to 25°E	-6.99	23	-5.01	25
IGC_1962_Congo_TM_Zone_26	3325	Congo DR (Zaire) - 6th parallel south 25°E to 27°E	-7.26	25	-4.23	27
IGC_1962_Congo_TM_Zone_28	3326	Congo DR (Zaire) - 6th parallel south 27°E to 29°E	-7.36	27	-4.24	29
IGC_1962_Congo_TM_Zone_30	3327	Congo DR (Zaire) - 6th parallel south 29°E to 31°E	-6.04	29	-4.34	29.64
IGCB_1955_Congo_TM_Zone_12	3339	Congo DR (Zaire) - 11°E to 13°E onshore	-6.04	12.17	-4.67	13.01
IGCB_1955_Congo_TM_Zone_14	3340	Congo DR (Zaire) - 13°E to 15°E	-5.91	13	-4.28	15.01
IGCB_1955_Congo_TM_Zone_16	3341	Congo DR (Zaire) - Bas Congo east of 15°E	-5.87	14.99	-4.42	16.28
IGCB_1955_UTM_Zone_33S	3342	Congo DR (Zaire) - Bas Congo	-6.04	12.17	-4.28	16.28
IGM_1995_UTM_Zone_32N	3064	Italy - west of 12°E	36.53	5.94	47.04	12
IGM_1995_UTM_Zone_33N	3065	Italy - 12~E to 18~E	34.79	12	47.1	18
IGM95_UTM_Zone_34N	9716	Italy - east of 18°E	34.76	17.99	41.64	18.99
IGN53_Mare_UTM_58S	2995	New Caledonia - Mare - west of 168°E	-21.71	167.75	-21.32	168
IGN53_Mare_UTM_Zone_59S	3172	New Caledonia - Mare - east of 168°E	-21.71	168	-21.35	168.19
IGN56_Lifou_UTM_58S	2981	New Caledonia - Lifou	-21.24	166.98	-20.62	167.52
IGN63_Hiva_Oa_UTM_Zone_7S	3302	French Polynesia - Marquesas Islands - Hiva Oa and Tahuata	-10.08	-139.23	-9.64	-138.75
IGN72_Grande_Terre_UTM_58S	3060	New Caledonia - Grande Terre	-22.45	163.92	-20.03	167.09
IGN72_Nuku_Hiva_UTM_7S	2978	French Polynesia - Marquesas Islands - Nuku Hiva, Ua Huka and Ua Pou	-9.57	-140.31	-8.72	-139.44
IGN_Astro_1960_UTM_Zone_28N	3367	Mauritania - west of 12°W onshore	14.72	-17.08	23.46	-12
IGN_Astro_1960_UTM_Zone_29N	3368	Mauritania - 12°W to 6°W	14.75	-12	27.3	-6
IGN_Astro_1960_UTM_Zone_30N	3369	Mauritania - east of 6°W	15.49	-6	25.74	-4.8
IGRS_UTM_Zone_37N	3890	Iraq - west of 42°E	31.14	38.79	36.75	42
IGRS_UTM_Zone_38N	3891	Iraq - 42°E to 48°E	29.06	42	37.39	48
IGRS_UTM_Zone_39N	3892	Iraq - east of 48°E	29.6	48	31	48.75
Indian_1954_UTM_Zone_46N	23946	Myanmar (Burma) - onshore west of 96°E	15.66	92.2	27.14	96.01
Indian_1954_UTM_Zone_47N	23947	Asia - Myanmar and Thailand - 96°E to 102°E	5.63	95.99	28.55	102.01
Indian_1954_UTM_Zone_48N	23948	Thailand - onshore east of 102°E	6.02	102	18.44	105.64
Indian_1960_TM_106NE	3176	Vietnam - offshore Cuu Long basin	7.99	106.54	11.15	110
Indian_1960_UTM_Zone_48N	3148	Asia - Cambodia and Vietnam - west of 108°E	8.33	102.14	23.4	108
Indian_1960_UTM_Zone_49N	3149	Vietnam - east of 108°E onshore	10.43	108	21.56	109.53
Indian_1975_UTM_Zone_47N	24047	Thailand - onshore and GoT 96°E to102°E	5.63	97.34	20.46	102.01
Indian_1975_UTM_Zone_48N	24048	Thailand - east of 102°E	6.02	102	18.44	105.64
Indonesian_1974_UTM_Zone_46N	23846	Indonesia - west of 96°E onshore	2.55	95.16	5.97	96
Indonesian_1974_UTM_Zone_46S	23886	Indonesia - west of 96°E, S hemisphere	-5	88	0	96
Indonesian_1974_UTM_Zone_47N	23847	Indonesia - 96°E to 102°E, N hemisphere onshore	0	96	5.42	102
Indonesian_1974_UTM_Zone_47S	23887	Indonesia - 96°E to 102°E, S hemisphere onshore	-3.57	98.24	0	102
Indonesian_1974_UTM_Zone_48N	23848	Indonesia - 102°E to 108°E, N hemisphere onshore	0	102	4.11	108
Indonesian_1974_UTM_Zone_48S	23888	Indonesia - 102°E to 108°E, S hemisphere onshore	-7.79	102	0	108
Indonesian_1974_UTM_Zone_49N	23849	Indonesia - 108°E to 114°E, N hemisphere onshore	0	108	4.25	114
Indonesian_1974_UTM_Zone_49S	23889	Indonesia - 108°E to 114°E, S hemisphere onshore	-8.67	108	0	114
Indonesian_1974_UTM_Zone_50N	23850	Indonesia - 114°E to 120°E, N hemisphere onshore	0	114	4.37	120
Indonesian_1974_UTM_Zone_50S	23890	Indonesia - 114°E to 120°E, S hemisphere onshore	-10.15	114	0	120
Indonesian_1974_UTM_Zone_51N	23851	Indonesia - 120°E to 126°E, N hemisphere onshore	0	120	3.84	125.71
Indonesian_1974_UTM_Zone_51S	23891	Indonesia - 120°E to 126°E, S hemisphere onshore	-10.98	120	0	126
Indonesian_1974_UTM_Zone_52N	23852	Indonesia - 126°E to 132°E, N hemisphere onshore	0	126.55	4.59	131
Indonesian_1974_UTM_Zone_52S	23892	Indonesia - 126°E to 132°E, S hemisphere onshore	-8.41	126	0	132
Indonesian_1974_UTM_Zone_53N	23853	Indonesia - 132°E to 138°E, N hemisphere	0	132	2	138
Indonesian_1974_UTM_Zone_53S	23893	Indonesia - 132°E to 138°E, S hemisphere onshore	-8.49	132	-0.29	138
Indonesian_1974_UTM_Zone_54S	23894	Indonesia - east of 138°E onshore	-9.19	138	-1.49	141.01
IRENET95_Irish_Transverse_Mercator	2157	Europe - Ireland (Republic and Ulster) - onshore	51.39	-10.56	55.43	-5.34
IRENET95_UTM_Zone_29N	2158	Europe - Ireland (Republic and Ulster) - onshore	51.39	-10.56	55.43	-5.34
ISN_1993_Lambert_1993	3057	Iceland	59.96	-30.87	69.59	-5.55
ISN_2004_LAEA_Europe	5638	Iceland	59.96	-30.87	69.59	-5.55
ISN_2004_Lambert_2004	5325	Iceland	59.96	-30.87	69.59	-5.55
ISN_2004_LCC_Europe	5639	Iceland	59.96	-30.87	69.59	-5.55
ISN2016_LAEA_Europe	9039	Iceland	59.96	-30.87	69.59	-5.55
ISN2016_Lambert_2016	8088	Iceland	59.96	-30.87	69.59	-5.55
ISN2016_LCC_Europe	9040	Iceland	59.96	-30.87	69.59	-5.55
Israeli_Grid_05	6984	Asia - Middle East - Israel and Palestine Territory onshore	29.45	34.17	33.28	35.69
Israeli_Grid_05-12	6991	Asia - Middle East - Israel and Palestine Territory onshore	29.45	34.17	33.28	35.69
Israel_TM_Grid	2039	Asia - Middle East - Israel and Palestine Territory onshore	29.45	34.17	33.28	35.69
JAD_2001_Jamaica_Grid	3448	Jamaica - onshore	17.64	-78.43	18.58	-76.17
JAD_2001_UTM_Zone_17N	3449	Jamaica - west of 78°W	14.16	-80.6	19.36	-77.99
JAD_2001_UTM_Zone_18N	3450	Jamaica - east of 78°W	14.08	-78	19.2	-74.51
Jamaica_1875_Old_Grid	24100	Jamaica - onshore	17.64	-78.43	18.58	-76.17
Jamaica_Grid	24200	Jamaica - onshore	17.64	-78.43	18.58	-76.17
Japan_Zone_1	30161	Japan - zone I	26.96	128.17	34.74	130.46
Japan_Zone_10	30170	Japan - zone X	37.73	139.49	41.58	142.14
Japan_Zone_11	30171	Japan - zone XI	41.34	139.34	43.42	141.46
Japan_Zone_12	30172	Japan - zone XII	42.15	140.89	45.54	143.61
Japan_Zone_13	30173	Japan - zone XIII	41.87	142.61	44.4	145.87
Japan_Zone_14	30174	Japan - zone XIV	24.67	141.2	27.8	142.33
Japan_Zone_15	30175	Japan - zone XV	26.02	126.63	26.91	128.4
Japan_Zone_16	30176	Japan - zone XVI	23.98	122.83	24.94	125.51
Japan_Zone_17	30177	Japan - zone XVII	24.4	131.12	26.01	131.38
Japan_Zone_18	30178	Japan - zone XVIII	20.37	136.02	20.48	136.16
Japan_Zone_19	30179	Japan - Minamitori- shima (Marcus Island) - onshore	24.22	153.91	24.35	154.05
Japan_Zone_2	30162	Japan - zone II	30.18	129.76	33.99	132.05
Japan_Zone_3	30163	Japan - zone III	33.72	130.81	36.38	133.49
Japan_Zone_4	30164	Japan - zone IV	32.69	131.95	34.45	134.81
Japan_Zone_5	30165	Japan - zone V	34.13	133.13	35.71	135.47
Japan_Zone_6	30166	Japan - zone VI	33.4	134.86	36.33	136.99
Japan_Zone_7	30167	Japan - zone VII	34.51	136.22	37.58	137.84
Japan_Zone_8	30168	Japan - zone VIII	34.54	137.32	38.58	139.91
Japan_Zone_9	30169	Japan - zone IX	29.31	138.4	37.98	141.11
JAXA_Snow_Depth_Polar_Stereographic_ North	5890	World - N hemisphere - north of 60°N	60	-180	90	180
JGD_2000_Japan_Zone_1	2443	Japan - zone I	26.96	128.17	34.74	130.46
JGD_2000_Japan_Zone_10	2452	Japan - zone X	37.73	139.49	41.58	142.14
JGD_2000_Japan_Zone_11	2453	Japan - zone XI	41.34	139.34	43.42	141.46
JGD_2000_Japan_Zone_12	2454	Japan - zone XII	42.15	140.89	45.54	143.61
JGD_2000_Japan_Zone_13	2455	Japan - zone XIII	41.87	142.61	44.4	145.87
JGD_2000_Japan_Zone_14	2456	Japan - zone XIV	24.67	141.2	27.8	142.33
JGD_2000_Japan_Zone_15	2457	Japan - zone XV	26.02	126.63	26.91	128.4
JGD_2000_Japan_Zone_16	2458	Japan - zone XVI	23.98	122.83	24.94	125.51
JGD_2000_Japan_Zone_17	2459	Japan - zone XVII	24.4	131.12	26.01	131.38
JGD_2000_Japan_Zone_18	2460	Japan - zone XVIII	20.37	136.02	20.48	136.16
JGD_2000_Japan_Zone_19	2461	Japan - Minamitori- shima (Marcus Island) - onshore	24.22	153.91	24.35	154.05
JGD_2000_Japan_Zone_2	2444	Japan - zone II	30.18	129.76	33.99	132.05
JGD_2000_Japan_Zone_3	2445	Japan - zone III	33.72	130.81	36.38	133.49
JGD_2000_Japan_Zone_4	2446	Japan - zone IV	32.69	131.95	34.45	134.81
JGD_2000_Japan_Zone_5	2447	Japan - zone V	34.13	133.13	35.71	135.47
JGD_2000_Japan_Zone_6	2448	Japan - zone VI	33.4	134.86	36.33	136.99
JGD_2000_Japan_Zone_7	2449	Japan - zone VII	34.51	136.22	37.58	137.84
JGD_2000_Japan_Zone_8	2450	Japan - zone VIII	34.54	137.32	38.58	139.91
JGD_2000_Japan_Zone_9	2451	Japan - zone IX	29.31	138.4	37.98	141.11
JGD_2000_UTM_Zone_51N	3097	Japan - 120°E to 126°E	21.1	122.38	29.71	126
JGD_2000_UTM_Zone_52N	3098	Japan - 126°E to 132°E	21.12	126	38.63	132
JGD_2000_UTM_Zone_53N	3099	Japan - 132°E to 138°E	17.09	132	43.55	138
JGD_2000_UTM_Zone_54N	3100	Japan - 138°E to 144°E	17.63	138	46.05	144
JGD_2000_UTM_Zone_55N	3101	Japan - 144°E to 150°E	23.03	144	45.65	147.86
JGD_2000_UTM_Zone_56N	102150	World - N hemisphere - 150°E to 156°E	0	150	84	156
JGD_2011_Japan_Zone_1	6669	Japan - zone I	26.96	128.17	34.74	130.46
JGD_2011_Japan_Zone_10	6678	Japan - zone X	37.73	139.49	41.58	142.14
JGD_2011_Japan_Zone_11	6679	Japan - zone XI	41.34	139.34	43.42	141.46
JGD_2011_Japan_Zone_12	6680	Japan - zone XII	42.15	140.89	45.54	143.61
JGD_2011_Japan_Zone_13	6681	Japan - zone XIII	41.87	142.61	44.4	145.87
JGD_2011_Japan_Zone_14	6682	Japan - zone XIV	24.67	141.2	27.8	142.33
JGD_2011_Japan_Zone_15	6683	Japan - zone XV	26.02	126.63	26.91	128.4
JGD_2011_Japan_Zone_16	6684	Japan - zone XVI	23.98	122.83	24.94	125.51
JGD_2011_Japan_Zone_17	6685	Japan - zone XVII	24.4	131.12	26.01	131.38
JGD_2011_Japan_Zone_18	6686	Japan - zone XVIII	20.37	136.02	20.48	136.16
JGD_2011_Japan_Zone_19	6687	Japan - Minamitori- shima (Marcus Island) - onshore	24.22	153.91	24.35	154.05
JGD_2011_Japan_Zone_2	6670	Japan - zone II	30.18	129.76	33.99	132.05
JGD_2011_Japan_Zone_3	6671	Japan - zone III	33.72	130.81	36.38	133.49
JGD_2011_Japan_Zone_4	6672	Japan - zone IV	32.69	131.95	34.45	134.81
JGD_2011_Japan_Zone_5	6673	Japan - zone V	34.13	133.13	35.71	135.47
JGD_2011_Japan_Zone_6	6674	Japan - zone VI	33.4	134.86	36.33	136.99
JGD_2011_Japan_Zone_7	6675	Japan - zone VII	34.51	136.22	37.58	137.84
JGD_2011_Japan_Zone_8	6676	Japan - zone VIII	34.54	137.32	38.58	139.91
JGD_2011_Japan_Zone_9	6677	Japan - zone IX	29.31	138.4	37.98	141.11
JGD_2011_UTM_Zone_51N	6688	Japan - 120°E to 126°E	21.1	122.38	29.71	126
JGD_2011_UTM_Zone_52N	6689	Japan - 126°E to 132°E	21.12	126	38.63	132
JGD_2011_UTM_Zone_53N	6690	Japan - 132°E to 138°E	17.09	132	43.55	138
JGD_2011_UTM_Zone_54N	6691	Japan - 138°E to 144°E	17.63	138	46.05	144
JGD_2011_UTM_Zone_55N	6692	Japan - 144°E to 150°E	23.03	144	45.65	147.86
JGD_2011_UTM_Zone_56N	102598	World - N hemisphere - 150°E to 156°E	0	150	84	156
Jordan_JTM	102158	Jordan	29.18	34.88	33.38	39.31
Kalianpur_1880_India_Zone_0	24370	Pakistan - north of 35°35'N	35.58	71.18	37.07	77.01
Kalianpur_1880_India_Zone_I	24371	Asia - India; Pakistan - 28°N to 35°35'N	28	60.86	35.59	81.64
Kalianpur_1880_India_Zone_IIa	24372	Asia - India; Pakistan - onshore 21°N to 28°N and west of 82°E	21	61.59	28.01	82.01
Kalianpur_1880_India_Zone_IIb	24382	Asia - Bangladesh; India; Myanmar; Pakistan - zone Ilb	21	82	29.47	101.17
Kalianpur_1880_India_Zone_III	24373	India - onshore 15°N to 21°N	15	70.14	21.01	87.15
Kalianpur_1880_India_Zone_IV	24374	India - mainland south of 15°N	8.02	73.94	15.01	80.4
Kalianpur_1937_India_Zone_IIb	24375	Bangladesh - onshore	20.52	88.01	26.64	92.67
Kalianpur_1937_UTM_Zone_45N	24305	Bangladesh - onshore west of 90°E	21.59	88.01	26.64	90
Kalianpur_1937_UTM_Zone_46N	24306	Bangladesh - onshore east of 90°E	20.52	90	25.29	92.67
Kalianpur_1962_India_Zone_I	24376	Pakistan - 28°N to 35°35'N	28	60.86	35.59	77.83
Kalianpur_1962_India_Zone_IIa	24377	Pakistan - onshore south of 28°N	23.64	61.59	28.01	71.91
Kalianpur_1962_UTM_Zone_41N	24311	Pakistan - onshore west of 66°E	24.98	60.86	29.87	66.01
Kalianpur_1962_UTM_Zone_42N	24312	Pakistan - onshore 66°E to 72°E	23.64	66	36.56	72.01
Kalianpur_1962_UTM_Zone_43N	24313	Pakistan - east of 72°E	28.21	72	37.07	77.83
Kalianpur_1975_India_Zone_I	24378	India - north of 28°N	28	70.35	35.51	81.64
Kalianpur_1975_India_Zone_IIa	24379	India - onshore 21°N to 28°N and west of 82°E	21	68.13	28.01	82.01
Kalianpur_1975_India_Zone_IIb	24380	India - onshore north of 21°N and east of 82°E	21	82	29.47	97.42
Kalianpur_1975_India_Zone_III	24381	India - onshore 15°N to 21°N	15	70.14	21.01	87.15
Kalianpur_1975_India_Zone_IV	24383	India - mainland south of 15°N	8.02	73.94	15.01	80.4
Kalianpur_1975_UTM_Zone_42N	24342	India - onshore west of 72°E	20.64	68.13	28.22	72.01
Kalianpur_1975_UTM_Zone_43N	24343	India - mainland 72°E to 78°E	8.02	72	35.51	78.01
Kalianpur_1975_UTM_Zone_44N	24344	India - onshore 78°E to 84°E	8.29	78	35.5	84.01
Kalianpur_1975_UTM_Zone_45N	24345	India - onshore 84°E to 90°E	18.18	84	28.14	90.01
Kalianpur_1975_UTM_Zone_46N	24346	India - mainland 90°E to 96°E	21.94	90	29.42	96.01
Kalianpur_1975_UTM_Zone_47N	24347	India - east of 96°E	27.1	96	29.47	97.42
Kandawala_Ceylon_Belt_Indian_Yards_ 1937	102064	Sri Lanka	2.58	77.02	11.45	85.24
Kandawala_Ceylon_Belt_Meters	102063	Sri Lanka	2.58	77.02	11.45	85.24
Kandawala_Sri_Lanka_Grid	5234	Sri Lanka - onshore	5.86	79.64	9.88	81.95
Karbala_1979_Iraq_National_Grid	6646	Iraq - onshore	29.06	38.79	37.39	48.61
Karbala_1979_Polservice_UTM_Zone_ 37N	3391	Iraq - west of 42°E	31.14	38.79	36.75	42
Karbala_1979_Polservice_UTM_Zone_ 38N	3392	Iraq - 42°E to 48°E	29.06	42	37.39	48
Karbala_1979_Polservice_UTM_Zone_ 39N	3393	Iraq - east of 48°E onshore	29.87	48	31	48.61
Kasai_1953_Congo_TM_Zone_22	3316	Congo DR (Zaire) - 6th parallel south 21°E to 23°E	-7.31	21	-5.31	23
Kasai_1953_Congo_TM_Zone_24	3317	Congo DR (Zaire) - 6th parallel south 23°E to 25°E	-6.99	23	-5.01	25
Katanga_1955_Katanga_Gauss_Zone_A	3986	Congo DR (Zaire) - Katanga east of 28.5°E	-13.46	28.5	-4.99	30.78
Katanga_1955_Katanga_Gauss_Zone_B	3987	Congo DR (Zaire) - Katanga 26.5°E to 29.5°E	-13.44	26.5	-4.99	29.5
Katanga_1955_Katanga_Gauss_Zone_C	3988	Congo DR (Zaire) - Katanga 24.5°E to 27.5°E	-12.08	24.5	-4.99	27.5
Katanga_1955_Katanga_Gauss_Zone_D	3989	Congo DR (Zaire) - Katanga west of 25.5°E	-11.72	21.74	-6.32	25.51
Katanga_1955_Katanga_Lambert	4415	Congo DR (Zaire) - Katanga	-13.46	21.74	-4.99	30.78
Katanga_1955_Katanga_TM	3315	Congo DR (Zaire) - Katanga	-13.46	21.74	-4.99	30.78
Kerguelen_Island_1949_UTM_42S	3336	French Southern Territories - Kerguelen onshore	-49.78	68.69	-48.6	70.62
Kertau_1968_Johor_Grid	4390	Malaysia - West Malaysia - Johor	1.21	102.44	2.95	104.6
Kertau_1968_Kedah_and_Perlis_Grid	4396	Malaysia - West Malaysia - Kedah and Perlis	5.08	99.59	6.72	101.12
Kertau_1968_Kelantan_Grid	4398	Malaysia - West Malaysia - Kelantan	4.54	101.33	6.29	102.67
Kertau_1968_Pahang_Grid	4392	Malaysia - West Malaysia - Pahang	2.45	101.33	4.78	103.67
Kertau_1968_Perak_Revised_Grid	4397	Malaysia - West Malaysia - Perak	3.66	100.07	5.92	102
Kertau_1968_Pinang_Grid	4395	Malaysia - West Malaysia - Pulau Pinang	5.12	100.12	5.59	100.56
Kertau_1968_Selangor_Grid	4393	Malaysia - West Malaysia - Selangor	2.54	100.76	3.87	101.97
Kertau_1968_Sembilan_and_Melaka_ Grid	4391	Malaysia - West Malaysia - Sembilan and Melaka	2.03	101.7	3.28	102.71
Kertau_1968_Terengganu_Grid	4394	Malaysia - West Malaysia - Terengganu	3.89	102.38	5.9	103.72
Kertau_RSO_Malaya_Chains	24571	Malaysia - West Malaysia - onshore	1.21	99.59	6.72	104.6
Kertau_RSO_Malaya_Meters	102062	Malaysia - West Malaysia - onshore	1.21	99.59	6.72	104.6
Kertau_RSO_RSO_Malaya	3168	Malaysia - West Malaysia - onshore	1.21	99.59	6.72	104.6
Kertau_RSO_RSO_Malaya_ ChSears1922trunc	3167	Malaysia - West Malaysia - onshore	1.21	99.59	6.72	104.6
Kertau_Singapore_Grid	24500	Singapore	1.13	103.59	1.47	104.07
Kertau_UTM_Zone_47N	24547	Malaysia - West Malaysia - onshore west of 102°E	2.29	99.59	6.72	102.01
Kertau_UTM_Zone_48N	24548	Malaysia - West Malaysia - east of 102°E	1.21	102	7.81	105.82
KKJ_Finland_Zone_0	3386	Finland - west of 19.5°E onshore	60.08	19.24	60.34	19.5
KKJ_Finland_Zone_5	3387	Finland - east of 31.5°E	62.83	31.5	63	31.59
KOC_Lambert	24600	Kuwait - onshore	28.53	46.54	30.09	48.48
Korea_2000_Korea_Central_Belt	5181	Korea, Republic of (South Korea) - 126°E to 128°E mainland	33.96	126	38.33	128
Korea_2000_Korea_Central_Belt_2010	5186	Korea, Republic of (South Korea) - 126°E to 128°E onshore	33.14	126	38.33	128
Korea_2000_Korea_Central_Belt_Jeju	5182	Korea, Republic of (South Korea) - 126°E to 128°E Jeju	33.14	126.09	33.61	127.01
Korea_2000_Korea_East_Belt	5183	Korea, Republic of (South Korea) - east of 128°E onshore	34.49	128	38.64	129.65
Korea_2000_Korea_East_Belt_2010	5187	Korea, Republic of (South Korea) - east of 128°E onshore	34.49	128	38.64	129.65
Korea_2000_Korea_East_Sea_Belt	5184	Korea, Republic of (South Korea) - 130°E to 132°E onshore	37.39	130.71	37.62	131.01
Korea_2000_Korea_East_Sea_Belt_2010	5188	Korea, Republic of (South Korea) - 130°E to 132°E onshore	37.39	130.71	37.62	131.01
Korea_2000_Korea_Unified_Coordinate_ System	5179	Korea, Republic of (South Korea)	28.6	122.71	40.27	134.28
Korea_2000_Korea_West_Belt	5180	Korea, Republic of (South Korea) - 124°E to 126°E onshore	33.99	124.53	38.04	126
Korea_2000_Korea_West_Belt_2010	5185	Korea, Republic of (South Korea) - 124°E to 126°E onshore	33.99	124.53	38.04	126
Korean_1985_Korea_Central_Belt	2097	Korea, Republic of (South Korea) - 126°E to 128°E mainland	33.96	126	38.33	128
Korean_1985_Korea_Central_Belt_Jeju	5168	Korea, Republic of (South Korea) - 126°E to 128°E Jeju	33.14	126.09	33.61	127.01
Korean_1985_Korea_East_Belt	2096	Korea, Republic of (South Korea) - east of 128°E onshore	34.49	128	38.64	129.65
Korean_1985_Korea_East_Sea_Belt	5167	Korea, Republic of (South Korea) - 130°E to 132°E onshore	37.39	130.71	37.62	131.01
Korean_1985_Korea_Unified_Coordinate _System	5178	Korea, Republic of (South Korea) - onshore	33.14	124.53	38.64	131.01
Korean_1985_Korea_West_Belt	2098	Korea, Republic of (South Korea) - 124°E to 126°E onshore	33.99	124.53	38.04	126
Korean_1985_Modified_Korea_Central_ Belt	5174	Korea, Republic of (South Korea) - 126°E to 128°E mainland	33.96	126	38.33	128
Korean_1985_Modified_Korea_Central_ Belt_Jeju	5175	Korea, Republic of (South Korea) - 126°E to 128°E Jeju	33.14	126.09	33.61	127.01
Korean_1985_Modified_Korea_East_Belt	5176	Korea, Republic of (South Korea) - east of 128°E onshore	34.49	128	38.64	129.65
Korean_1985_Modified_Korea_East_Sea_ Belt	5177	Korea, Republic of (South Korea) - 130°E to 132°E onshore	37.39	130.71	37.62	131.01
Korean_1985_Modified_Korea_West_ Belt	5173	Korea, Republic of (South Korea) - 124°E to 126°E onshore	33.99	124.53	38.04	126
KOSOVAREF01_Balkans_Zone_7	9141	Kosovo	41.85	19.97	43.25	21.8
Kousseri_UTM_Zone_33N	2313	Cameroon - N'Djamena area	11.7	14.17	12.77	15.09
KUDAMS_KTM	31901	Kuwait - Kuwait City	29.17	47.78	29.45	48.16
Kyrg-06_TM_Zone_1	7692	Kyrgyz Republic - 67°01'E to 70°01'E	39.4	67.017	40.3	70.017
Kyrg-06_TM_Zone_2	7693	Kyrgyz Republic - 70°01'E to 73°01'E	39.133	70.017	42.9	73.017
Kyrg-06_TM_Zone_3	7694	Kyrgyz Republic - 73°01'E to 76°01'E	39.25	73.017	43.333	76.017
Kyrg-06_TM_Zone_4	7695	Kyrgyz Republic - 76°01'E to 79°01'E	40.167	76.017	43	79.017
Kyrg-06_TM_Zone_5	7696	Kyrgyz Republic - 79°01'E to 82°01'E	41.5	79.017	43	82.017
La_Canoa_UTM_Zone_18N	24718	Venezuela - west of 72°W	7.02	-73.38	11.62	-71.99
La_Canoa_UTM_Zone_19N	24719	Venezuela - 72°W and 66°W onshore	0.73	-72	12.25	-66
La_Canoa_UTM_Zone_20N	24720	Venezuela - east of 66°W onshore	0.64	-66	11.23	-59.8
La_Canoa_UTM_Zone_21N	24721	Venezuela - east of 60°W, N hemisphere	7.6	-61	10	-58
Lake_Maracaibo_Grid	2102	Venezuela - Maracaibo area	10	-72.25	11	-71.5
Lake_Maracaibo_Grid_M1	2101	Venezuela - Maracaibo area	10	-72.25	11	-71.5
Lake_Maracaibo_Grid_M3	2103	Venezuela - Maracaibo area	10	-72.25	11	-71.5
Lake_Maracaibo_La_Rosa_Grid	2104	Venezuela - Maracaibo - blocks I II and III	10	-71.5	10.51	-71.17
Le_Pouce_1934_Mauritius_Grid	3337	Mauritius - mainland	-20.57	57.25	-19.94	57.85
LCC_Bangladesh	102951	Bangladesh	18.56	88.01	26.64	92.67
LCC_Gulshan	102952	Bangladesh	18.56	88.01	26.64	92.67
LGD2006_Libya_TM	3177	Libya	19.5	9.31	35.23	26.21
LGD2006_Libya_TM_Zone_10	3195	Libya - 18°E to 20°E onshore	21.54	18	32.17	20
LGD2006_Libya_TM_Zone_11	3196	Libya - 20°E to 22°E onshore	20.54	20	33	22
LGD2006_Libya_TM_Zone_12	3197	Libya - 22°E to 24°E onshore	19.5	22	32.97	24
LGD2006_Libya_TM_Zone_13	3198	Libya - east of 24°E onshore	19.99	24	32.15	25.21
LGD2006_Libya_TM_Zone_5	3190	Libya - west of 10°E	25.37	9.31	30.49	10.01
LGD2006_Libya_TM_Zone_6	3191	Libya - 10°E to 12°E onshore	23.51	10	33.23	12
LGD2006_Libya_TM_Zone_7	3192	Libya - 12°E to 14°E onshore	22.8	12	33.06	14
LGD2006_Libya_TM_Zone_8	3193	Libya - 14°E to 16°E onshore	22.61	14	32.79	16
LGD2006_Libya_TM_Zone_9	3194	Libya - 16°E to 18°E onshore	22.51	16	31.34	18.01
LGD2006_UTM_Zone_32N	3199	Libya - west of 12°E	23.51	9.31	33.92	12
LGD2006_UTM_Zone_33N	3201	Libya - 12°E to 18°E	22.51	12	35.23	18
LGD2006_UTM_Zone_34N	3202	Libya - 18°E to 24°E	19.5	17.99	35.03	24.01
LGD2006_UTM_Zone_35N	3203	Libya - east of 24°E	19.99	24	33.6	26.21
Lisboa_Bessel_Bonne	102163	Portugal	29.24	-35.58	43.07	-6.19
Lisboa_Hayford_Gauss_IGeoE	102164	Portugal	29.24	-35.58	43.07	-6.19
Lisboa_Hayford_Gauss_IPCC	102165	Portugal	29.24	-35.58	43.07	-6.19
Lisbon_Lisbon_Portuguese_Grid	20791	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
Lisbon_Portuguese_Grid_New	5018	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
Little_Cayman_1961_UTM_Zone_17N	3357	Cayman Islands - Little Cayman and Cayman Brac	19.63	-80.14	19.78	-79.69
LKS_1992_Latvia_TM	3059	Latvia	55.67	19.06	58.09	28.24
LKS_1992_Latvia_TM_0	102440	Latvia	55.67	19.06	58.09	28.24
LKS_1994_Lithuania_TM	3346	Lithuania	53.89	19.02	56.45	26.82
Locodjo_1965_TM_5_NW	2164	Cote d'Ivoire (Ivory Coast) - offshore	1.02	-7.55	5.19	-3.11
Locodjo_1965_UTM_Zone_29N	2042	Cote d'Ivoire (Ivory Coast) - west of 6°W	4.29	-8.61	10.74	-6
Locodjo_1965_UTM_Zone_30N	2040	Cote d'Ivoire (Ivory Coast) - east of 6°W	4.92	-6	10.46	-2.48
Lome_UTM_Zone_31N	25231	Togo	2.91	-0.15	11.14	2.42
London_Survey_Grid	102400	UK - London	51.2	-0.7	51.8	0.6
LUREF_Luxembourg_TM	2169	Luxembourg	49.44	5.73	50.19	6.53
Luzon_1911_UTM_Zone_50N	102453	Philippines - West of 120°E, N hemisphere	3	114	22	120
Luzon_1911_UTM_Zone_51N	102454	Philippines - 120°E to 126°E, N hemisphere	3	120	24	126
Luzon_1911_UTM_Zone_52N	102455	Philippines - East of 126°E, N hemisphere	4	126	20	132
Macao_1920_Macao_Grid	8433	China - Macao	22.06	113.52	22.23	113.68
Macao_2008_Macao_Grid	102448	Macao	22.1	113.52	22.22	113.6
Macedonian_State_Coordinate_System	6204	North Macedonia	40.85	20.45	42.36	23.04
Madeira_1936_UTM_Zone_28N	2191	Portugal - Madeira archipelago onshore	32.35	-17.31	33.15	-16.23
Madrid_1870_Madrid_Spain	2062	Spain - mainland onshore	35.95	-9.37	43.82	3.39
MAGNA-SIRGAS_CMT12	103599	Colombia	-4.23	-84.77	15.51	-66.87
MAGNA_Arauca_2007	6244	Colombia - Arauca - Arauca	6.583	-71.267	7.6	-70.25
MAGNA_Armenia_Quindio_2006	6245	Colombia - Armenia - Quindio	4.017	-76.183	5.033	-75.167
MAGNA_Barranquilla_Atlantico_1997	6246	Colombia - Barranquilla - Atlantico	10.417	-75.35	11.433	-74.333
MAGNA_Bogota_DC_2005	6247	Colombia - Bogota D.C. - Bogota D.C.	4.167	-74.65	5.183	-73.633
MAGNA_Bucaramanga_Santander_2008	6248	Colombia - Bucaramanga - Santander	6.567	-73.7	7.583	-72.683
MAGNA_Cali_Valle_del_Cauca_2009	6249	Colombia - Cali - Valle del Cauca	2.933	-77.033	3.95	-76.017
MAGNA_Cartagena_Bolivar_2005	6250	Colombia - Cartagena_Bolivar	9.883	-76.017	10.9	-75
MAGNA_Ciudad_Bogota	102233	Colombia region 8	-4.23	-74.4	7.1	-66.87
MAGNA_Colombia_Bogota	3116	Colombia - 75°35'W to 72°35'W	-2.51	-75.59	11.82	-72.58
MAGNA_Colombia_Este	3117	Colombia - 72°35'W to 69°35'W	-4.23	-72.59	12.52	-69.58
MAGNA_Colombia_Este_Este	3118	Colombia - east of 69°35'W	-2.25	-69.59	6.31	-66.87
MAGNA_Colombia_Oeste	3115	Colombia - 78°35'W to 75°35'W	0.03	-78.59	10.21	-75.58
MAGNA_Colombia_Oeste_Oeste	3114	Colombia - west of 78°35'W	1.23	-79.1	2.48	-78.58
MAGNA_Cucuta_Norte_de_Santander_ 2011	6251	Colombia - Cucuta - Norte de Santander	7.383	-73.017	8.4	-72
MAGNA_Florencia_Caqueta_2007	6252	Colombia - Florencia - Caqueta	1.117	-76.133	2.133	-75.117
MAGNA_Ibague_Tolima_2007	6253	Colombia - Ibague - Tolima	3.917	-75.683	4.933	-74.667
MAGNA_Inirida_Guainia_2008	6254	Colombia - Inirida - Guainia	3.333	-68.417	4.35	-67.4
MAGNA_Leticia_Amazonas_1994	6255	Colombia - Leticia - Amazonas	-4.7	-70.45	-3.683	-69.433
MAGNA_Manizales_Caldas_2011	6256	Colombia - Manizales - Caldas	4.567	-76.017	5.583	-75
MAGNA_Medellin_Antioquia_2010	6257	Colombia - Medellin - Antioquia	5.717	-76.067	6.733	-75.05
MAGNA_Mitu_Vaupes_2011	6258	Colombia - Mitu - Vaupes	0.733	-70.75	1.75	-69.733
MAGNA_Mocoa_Putumayo_2011	6259	Colombia - Mocoa - Putumayo	0.633	-77.167	1.65	-76.15
MAGNA_Monteria_Cordoba_2006	6260	Colombia - Monteria - Cordoba	8.267	-76.383	9.283	-75.367
MAGNA_Neiva_Huila_2006	6261	Colombia - Neiva - Huila	2.433	-75.8	3.45	-74.783
MAGNA_Pasto_Narino_2008	6262	Colombia - Pasto - Narino	0.7	-77.767	1.717	-76.75
MAGNA_Pereira_Risaralda_2007	6263	Colombia - Pereira - Risaralda	4.3	-76.2	5.317	-75.183
MAGNA_Popayan_Cauca_2006	6264	Colombia - Popayan - Cauca	2.95	-77.117	2.967	-76.1
MAGNA_Puerto_Carreno_Vichada_2011	6265	Colombia - Puerto - Carreno - Vichada	5.667	-68.017	6.683	-67
MAGNA_Quibdo_Choco_2011	6266	Colombia - Quibdo - Choco	5.183	-77.167	6.2	-76.15
MAGNA_Riohacha_La_Guajira_2006	6267	Colombia - Riohacha - La Guajira	11.033	-73.417	12.05	-72.4
MAGNA_San_Andres_2007	6268	Colombia - San_Andres - San_Andres	12.017	-82.233	13.033	-81.217
MAGNA_San_Jose_del_Guaviare_2011	6269	Colombia - San Jose del Guaviare - Guaviare	2.05	-73.15	3.067	-72.133
MAGNA_Santa_Marta_Magdalena_2007	6270	Colombia - Santa Marta - Magdalena	10.717	-74.733	11.733	-73.717
MAGNA_Sucre_2006	6271	Colombia - Sucre - Sucre	8.3	-75.233	9.317	-74.217
MAGNA_Tunja_Boyaca_1997	6272	Colombia - Tunja - Boyaca	5.033	-73.867	6.05	-72.85
MAGNA_Valledupar_Cesar_2011	6273	Colombia - Valledupar - Cesar	9.933	-73.583	10.95	-73.567
MAGNA_Villavicencio_Meta_2011	6274	Colombia - Villavicencio - Meta	3.65	-74.133	4.667	-73.117
MAGNA_Yopal_Casanare_2006	6275	Colombia - Yopal - Casanare	4.85	-72.933	5.867	-71.917
Makassar_Jakarta_NEIEZ	5331	Indonesia - Sulawesi SW	-6.54	118.71	-1.88	120.78
Makassar_NEIEZ	3002	Indonesia - Sulawesi SW	-6.54	118.71	-1.88	120.78
Malongo_1987_UTM_Zone_32S	25932	Africa - Angola (Cabinda) and DR Congo (Zaire) - offshore	-6.04	10.53	-5.05	12.37
Malongo_1987_UTM_zone_33S	7992	DR Congo (Zaire) - offshore	-6.04	11.79	-5.79	12.37
Manoca_1962_UTM_Zone_32N	2215	Cameroon - coastal area	2.16	8.45	4.99	10.4
MARGEN_UTM_Zone_19S	5356	Bolivia - west of 66°W	-22.91	-69.66	-9.77	-66
MARGEN_UTM_Zone_20S	5355	Bolivia - 66°W to 60°W	-22.87	-66	-9.67	-60
MARGEN_UTM_Zone_21S	5357	Bolivia - east of 60°W	-20.17	-60	-16.27	-57.52
Mars_2000_Equidistant_Cylindrical_sphe re	103885	World	-90	-180	90	180
Mars_2000_North_Pole_Stereographic_ sphere	103883	World - N hemisphere - north of 60~N	60	-180	90	180
Mars_2000_Sinusoidal_sphere	103886	World	-90	-180	90	180
Mars_2000_South_Pole_Stereographic_ sphere	103884	World - S hemisphere - south of 60~S	-90	-180	-60	180
Mars_2000_Winkel_Tripel_sphere	103887	World	-90	-180	90	180
Massawa_UTM_Zone_37N	26237	Eritrea	12.36	36.44	18.1	43.31
Maupiti_1983_UTM_Zone_5S	3306	French Polynesia - Society Islands - Maupiti	-16.57	-152.39	-16.34	-152.14
Mauritania_1999_UTM_Zone_28N	3343	Mauritania - 18°W to 12°W	14.72	-18	23.46	-12
Mauritania_1999_UTM_Zone_29N	3344	Mauritania - 12°W to 6°W	14.75	-12	27.3	-6
Mauritania_1999_UTM_Zone_30N	3345	Mauritania - east of 6°W	15.49	-6	25.74	-4.8
Merchich_Degree_UTM_Zone_28N	102144	Western Sahara	18.98	-20.68	27.67	-8.66
Merchich_Sahara_Nord	26194	Western Sahara - north of 24.3°N	24.29	-15.42	27.67	-8.66
Merchich_Sahara_Sud	26195	Western Sahara - south of 24.3°N	20.71	-17.16	24.31	-12
Mexican_Datum_1993_UTM_Zone_11N	4484	Mexico - west of 114°W	15.01	-122.19	32.72	-114
Mexican_Datum_1993_UTM_Zone_12N	4485	Mexico - 114°W to 108°W	15.09	-114	32.27	-108
Mexican_Datum_1993_UTM_Zone_13N	4486	Mexico - 108°W to 102°W	14.05	-108	31.79	-102
Mexican_Datum_1993_UTM_Zone_14N	4487	Mexico - 102°W to 96°W	12.3	-102	29.81	-96
Mexican_Datum_1993_UTM_Zone_15N	4488	Mexico - 96°W to 90°W	12.1	-96	26	-90
Mexican_Datum_1993_UTM_Zone_16N	4489	Mexico - east of 90°W	17.81	-90	25.77	-84.64
Mexico_ITRF2008_LCC	6372	Mexico	12.1	-122.19	32.72	-84.64
Mexico_ITRF2008_UTM_Zone_11N	6366	Mexico - west of 114°W	15.01	-122.19	32.72	-114
Mexico_ITRF2008_UTM_Zone_12N	6367	Mexico - 114°W to 108°W	15.09	-114	32.27	-108
Mexico_ITRF2008_UTM_Zone_13N	6368	Mexico - 108°W to 102°W	14.05	-108	31.79	-102
Mexico_ITRF2008_UTM_Zone_14N	6369	Mexico - 102°W to 96°W	12.3	-102	29.81	-96
Mexico_ITRF2008_UTM_Zone_15N	6370	Mexico - 96°W to 90°W	12.1	-96	26	-90
Mexico_ITRF2008_UTM_Zone_16N	6371	Mexico - east of 90°W	17.81	-90	25.77	-84.64
Mexico_ITRF92_LCC	6362	Mexico	12.1	-122.19	32.72	-84.64
MGI_1901_Balkans_zone_5	8677	Europe - former Yugoslavia onshore west of 16.5°E	42.95	13.38	46.88	16.5
MGI_1901_Balkans_zone_6	8678	Europe - former Yugoslavia onshore 16.5°E to 19.5°E	41.79	16.5	46.55	19.51
MGI_1901_Balkans_zone_7	6316	Europe - former Yugoslavia onshore 19.5°E to 22.5°E	40.85	19.5	46.19	22.51
MGI_1901_Balkans_zone_8	8679	Europe - former Yugoslavia onshore east of 22.5°E	41.11	22.5	44.7	23.04
MGI_1901_Slovene_National_Grid	3912	Slovenia	45.42	13.38	46.88	16.61
MGI_1901_Slovenia_Grid	8686	Slovenia	45.42	13.38	46.88	16.61
MGI_3_Degree_Gauss_Zone_5	31265	Europe - former Yugoslavia onshore west of 16.5°E	42.95	13.38	46.88	16.5
MGI_3_Degree_Gauss_Zone_6	31266	Europe - former Yugoslavia onshore 16.5°E to 19.5°E	41.79	16.5	46.55	19.51
MGI_3_Degree_Gauss_Zone_7	31267	Europe - former Yugoslavia onshore 19.5°E to 22.5°E	40.85	19.5	46.19	22.51
MGI_3_Degree_Gauss_Zone_8	31268	Europe - former Yugoslavia onshore east of 22.5°E	41.11	22.5	44.7	23.04
MGI_Austria_Central	9272	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_Austria_East	9273	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_Austria_GK_Central	31255	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_Austria_GK_East	31256	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_Austria_GK_M28	31257	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_Austria_GK_M31	31258	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_Austria_GK_M34	31259	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_Austria_GK_West	31254	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_Austria_Lambert	31287	Austria	46.4	9.53	49.02	17.17
MGI_Austria_West	9271	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_Balkans_5	31275	Europe - former Yugoslavia onshore west of 16.5°E	42.95	13.38	46.88	16.5
MGI_Balkans_6	31276	Europe - former Yugoslavia onshore 16.5°E to 19.5°E	41.79	16.5	46.55	19.51
MGI_Balkans_7	31277	Europe - former Yugoslavia onshore 19.5°E to 22.5°E	40.85	19.5	46.19	22.51
MGI_Balkans_8	31279	Europe - former Yugoslavia onshore east of 22.5°E	41.11	22.5	44.7	23.04
MGI_Ferro_Austria_GK_Central	31252	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_Ferro_Austria_GK_East	31253	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_Ferro_Austria_GK_West	31251	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_Ferro_M28	31288	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_Ferro_M31	31289	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_Ferro_M34	31290	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_M28	31284	Austria - west of 11°50'E	46.77	9.53	47.61	11.84
MGI_M31	31285	Austria - 11°50'E to 14°50'E	46.4	11.83	48.79	14.84
MGI_M34	31286	Austria - east of 14°50'E	46.56	14.83	49.02	17.17
MGI_Slovenia_Grid	2170	Slovenia	45.42	13.38	46.88	16.61
Mhast_Offshore_UTM_Zone_32S	3354	Africa - Angola (Cabinda) and DR Congo (Zaire) - offshore	-6.04	10.53	-5.05	12.37
Mhast_Onshore_UTM_Zone_32S	3353	Africa - Angola (Cabinda) and DR Congo (Zaire) - coastal	-6.04	10.53	-4.38	13.1
Minna_UTM_Zone_31N	26331	Nigeria - offshore deep water - west of 6°E	1.92	2.66	6.14	6
Minna_UTM_Zone_32N	26332	Nigeria - offshore deep water - east of 6°E	2.61	6	3.68	7.82
MML07_Grid	9373	UK - London to Sheffield	51.46	-1.89	53.41	0.15
MMN_Argentina_2	9252	Argentina - Tierra del Fuego onshore	-55.11	-68.64	-52.59	-63.73
MMS_Argentina_2	9254	Argentina - Tierra del Fuego onshore	-55.11	-68.64	-52.59	-63.73
MOLDREF99_Moldova_TM	4026	Moldova	45.44	26.63	48.47	30.13
MONREF_1997_UTM_Zone_46N	102224	Mongolia - west of 96°E	43.01	87.76	50.89	96
MONREF_1997_UTM_Zone_47N	102225	Mongolia - between 96°E and 102°E	42.14	96	52.15	102
MONREF_1997_UTM_Zone_48N	102226	Mongolia - between 102°E and 108°E	41.58	102	51.42	108
MONREF_1997_UTM_Zone_49N	102227	Mongolia - between 108°E and 114°E	42.35	108	50.23	114
MONREF_1997_UTM_Zone_50N	102228	Mongolia - east of 114°E	44.9	114	50.32	119.94
Monte_Mario_Italy_1	3003	Italy - west of 12°E	36.53	5.94	47.04	12
Monte_Mario_Italy_2	3004	Italy - east of 12°E	34.76	12	47.1	18.99
Monte_Mario_Rome_Italy_1	26591	Italy - west of 12°E	36.53	5.94	47.04	12
Monte_Mario_Rome_Italy_2	26592	Italy - east of 12°E	34.76	12	47.1	18.99
Monte_Mario_TM_Emilia-Romagna	5659	Italy - Emilia-Romagna	43.73	9.19	45.14	12.76
Montserrat_1958_British_West_Indies_ Grid	2004	Montserrat - onshore	16.62	-62.29	16.87	-62.08
Moon_2000_Equidistant_Cylindrical	103881	World	-90	-180	90	180
Moon_2000_Far_Side_Lambert_Azimuth al_Equal_Area	103879	Moon - Far Side	-90	90	90	-90
Moon_2000_Near_Side_Lambert_ Azimuthal_Equal_Area	103880	Moon - Near Side	-90	-90	90	90
Moon_2000_North_Pole_Stereographic	103877	World - N hemisphere - north of 60~N	60	-180	90	180
Moon_2000_Sinusoidal	103882	World	-90	-180	90	180
Moon_2000_South_Pole_Stereographic	103878	World - S hemisphere - south of 60~S	-90	-180	-60	180
Moorea_1987_UTM_Zone_6S	3305	French Polynesia - Society Islands - Moorea	-17.63	-150	-17.41	-149.73
MOP78_UTM_1S	2988	Wallis and Futuna - Wallis	-13.41	-176.25	-13.16	-176.07
Mount_Dillon_Tobago_Grid	2066	Trinidad and Tobago - Tobago - onshore	11.08	-60.9	11.41	-60.44
Moznet_UTM_Zone_36S	3036	Mozambique - west of 36°E	-27.58	30.21	-11.41	36
Moznet_UTM_Zone_37S	3037	Mozambique - 36°E to 42°E	-27.71	36	-10.09	42
Moznet_UTM_Zone_38S	5629	Mozambique - onshore east of 36°E	-18.98	35.99	-10.42	40.9
Mporaloko_UTM_Zone_32N	26632	Gabon - north of equator and west of 12°E onshore	0	9.25	2.32	12
Mporaloko_UTM_Zone_32S	26692	Gabon - west of 12°E	-6.37	7.03	2.32	12.01
MTRF-2000_UTM_zone_36N	8836	Saudi Arabia - west of 36°E	24.92	34.44	29.38	36.01
MTRF-2000_UTM_zone_37N	8837	Saudi Arabia - 36°E to 42°E	16.29	36	32.16	42
MTRF-2000_UTM_zone_38N	8838	Saudi Arabia - 42°E to 48°E	16.35	41.99	31.15	48
MTRF-2000_UTM_zone_39N	8839	Saudi Arabia - 48°E to 54°E	17.94	47.99	28.94	54.01
MTRF-2000_UTM_zone_40N	8840	Saudi Arabia - east of 54°E	19.66	54	22.77	55.67
NAD_1927_10TM_AEP_Forest	102178	Canada - Alberta	48.99	-120	60	-109.98
NAD_1927_10TM_AEP_Resource	102179	Canada - Alberta	48.99	-120	60	-109.98
NAD_1927_3TM_111	3771	Canada - Alberta - east of 112.5°W	48.99	-112.5	60	-109.98
NAD_1927_3TM_114	3772	Canada - Alberta - 115.5°W to 112.5°W	48.99	-115.5	60	-112.5
NAD_1927_3TM_117	3773	Canada - Alberta - 118.5°W to 115.5°W	50.77	-118.5	60	-115.5
NAD_1927_3TM_120	3800	Canada - Alberta - west of 118.5°W	52.88	-120	60	-118.5
NAD_1927_Alaska_Albers_Feet	2964	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1927_Alaska_Albers_Meters	102117	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1927_BLM_Zone_10N	4410	USA - 126°W to 120°W	30.54	-126	49.09	-119.99
NAD_1927_BLM_Zone_11N	4411	USA - 120°W to 114°W	30.88	-120	49.01	-114
NAD_1927_BLM_Zone_12N	4412	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1927_BLM_Zone_13N	4413	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1927_BLM_Zone_14N	32064	USA - 102°W to 96°W and GoM OCS	25.83	-102	49.01	-95.87
NAD_1927_BLM_Zone_15N	32065	USA - 96°W to 90°W and GoM OCS	25.61	-96.01	49.38	-89.86
NAD_1927_BLM_Zone_16N	32066	USA - 90°W to 84°W and GoM OCS	23.95	-90.01	48.32	-83.91
NAD_1927_BLM_Zone_17N	32067	USA - 84°W to 78°W and GoM OCS	23.81	-84.09	46.13	-77.99
NAD_1927_BLM_Zone_18N	4418	USA - 78°W to 72°W	28.28	-78	45.03	-72
NAD_1927_BLM_Zone_19N	4419	USA - 72°W to 66°W	33.61	-72	47.47	-65.99
NAD_1927_BLM_Zone_1N	4401	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1927_BLM_Zone_2N	4402	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1927_BLM_Zone_3N	4403	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1927_BLM_Zone_4N	4404	USA - 162°W to 156°W - AK, OCS	50.98	-162	74.71	-155.99
NAD_1927_BLM_Zone_59N	4399	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1927_BLM_Zone_5N	4405	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1927_BLM_Zone_60N	4400	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1927_BLM_Zone_6N	4406	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1927_BLM_Zone_7N	4407	USA - 144°W to 138°W	53.47	-144	73.59	-137.99
NAD_1927_BLM_Zone_8N	4408	USA - 138°W to 132°W	53.6	-138	73.04	-131.99
NAD_1927_BLM_Zone_9N	4409	USA - 132°W to 126°W	35.38	-132	56.84	-126
NAD_1927_California_Teale_Albers	3309	USA - California	32.53	-124.45	42.01	-114.12
NAD_1927_CGQ77_MTM_10_SCoPQ	2016	Canada - Quebec - west of 78°W	46.23	-79.85	62.45	-78
NAD_1927_CGQ77_MTM_2_SCoPQ	2008	Canada - Quebec - east of 57°W	46.6	-57	53.76	-54
NAD_1927_CGQ77_MTM_3_SCoPQ	2009	Canada - Quebec - east of 60°W	50.2	-60	52.01	-57.1
NAD_1927_CGQ77_MTM_4_SCoPQ	2010	Canada - Quebec - 63°W to 60°W	47.16	-63	52.01	-60
NAD_1927_CGQ77_MTM_5_SCoPQ	2011	Canada - Quebec - 66°W to 63°W	47.95	-66	60.42	-63
NAD_1927_CGQ77_MTM_6_SCoPQ	2012	Canada - Quebec - 69°W to 66°W	47.31	-69	59	-66
NAD_1927_CGQ77_MTM_7_SCoPQ	2013	Canada - Quebec - 72°W to 69°W	45.01	-72	61.8	-69
NAD_1927_CGQ77_MTM_8_SCoPQ	2014	Canada - Quebec - 75°W to 72°W	44.99	-75	62.53	-72
NAD_1927_CGQ77_MTM_9_SCoPQ	2015	Canada - Quebec - 78°W to 75°W	45.37	-78	62.62	-75
NAD_1927_CGQ77_Quebec_Lambert	2138	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1927_CGQ77_UTM_Zone_17N	2031	Canada - Quebec - west of 78°W	46.23	-79.85	62.45	-78
NAD_1927_CGQ77_UTM_Zone_18N	2032	Canada - Quebec - 78°W to 72°W	44.99	-78	62.62	-72
NAD_1927_CGQ77_UTM_Zone_19N	2033	Canada - Quebec - 72°W to 66°W	45.01	-72	61.8	-66
NAD_1927_CGQ77_UTM_Zone_20N	2034	Canada - Quebec - 66°W to 60°W	47.16	-66	60.42	-60
NAD_1927_CGQ77_UTM_Zone_21N	2035	Canada - Quebec - east of 60°W	50.2	-60	52.01	-57.1
NAD_1927_Contiguous_USA_Albers	5069	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
NAD_1927_Cuba_Norte	2085	Cuba - onshore north of 21°30'N	21.38	-85.01	23.25	-76.91
NAD_1927_Cuba_Sur	2086	Cuba - onshore south of 21°30'N	19.77	-78.69	21.5	-74.07
NAD_1927_DEF_1976_MTM_10	2019	Canada - Ontario - MTM zone 10	42.26	-81	47.33	-77.99
NAD_1927_DEF_1976_MTM_11	2020	Canada - Ontario - MTM zone 11	41.67	-83.6	46	-81
NAD_1927_DEF_1976_MTM_12	2021	Canada - Ontario - MTM zone 12	46	-82.5	55.21	-79.5
NAD_1927_DEF_1976_MTM_13	2022	Canada - Ontario - MTM zone 13	46	-85.5	55.59	-82.5
NAD_1927_DEF_1976_MTM_14	2023	Canada - Ontario - 88.5°W to 85.5°W	47.17	-88.5	56.7	-85.5
NAD_1927_DEF_1976_MTM_15	2024	Canada - Ontario - 91.5°W to 88.5°W	47.97	-91.5	56.9	-88.5
NAD_1927_DEF_1976_MTM_16	2025	Canada - Ontario - 94.5°W to 91.5°W	48.06	-94.5	55.2	-91.5
NAD_1927_DEF_1976_MTM_17	2026	Canada - Ontario - west of 94.5°W	48.69	-95.16	53.24	-94.5
NAD_1927_DEF_1976_MTM_8	2017	Canada - Ontario - east of 75°W	44.98	-75	45.65	-74.35
NAD_1927_DEF_1976_MTM_9	2018	Canada - Ontario - 78°W to 75°W	43.63	-78	46.25	-75
NAD_1927_DEF_1976_UTM_Zone_15N	2027	Canada - Ontario - west of 90°W	48.03	-95.16	56.2	-90
NAD_1927_DEF_1976_UTM_Zone_16N	2028	Canada - Ontario - 90°W to 84°W	46.11	-90	56.9	-84
NAD_1927_DEF_1976_UTM_Zone_17N	2029	Canada - Ontario - 84°W to 78°W	41.67	-84	55.37	-78
NAD_1927_DEF_1976_UTM_Zone_18N	2030	Canada - Ontario - east of 78°W	43.63	-78	46.25	-74.35
NAD_1927_Georgia_Statewide_Albers	102118	USA - Georgia	30.36	-85.61	35.01	-80.77
NAD_1927_Guatemala_Norte	32061	Guatemala - north of 15°51'30''N	15.85	-91.86	17.83	-88.34
NAD_1927_Guatemala_Sur	32062	Guatemala - south of 15°51'30''N	13.69	-92.29	15.86	-88.19
NAD_1927_Michigan_GeoRef_Feet_US	102120	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1927_Michigan_GeoRef_Meters	102122	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1927_MTM_1	32081	Canada - Newfoundland - east of 54.5°W	46.56	-54.5	49.89	-52.54
NAD27_MTM_zone_10	7991	Canada - Ontario - MTM zone 10	42.26	-81	47.33	-77.99
NAD_1927_MTM_2	32082	Canada - Newfoundland and Labrador - 57.5°W to 54.5°W	46.81	-57.5	54.71	-54.5
NAD_1927_MTM_3	32083	Canada - Newfoundland and Labrador - 60°W to 57.5°W	47.5	-59.48	50.54	-57.5
NAD_1927_MTM_4	32084	Canada - Labrador - 63°W to 60°W	52	-63	58.92	-60
NAD_1927_MTM_5	32085	Canada - Labrador - 66°W to 63°W	51.58	-66	60.52	-63
NAD_1927_MTM_6	32086	Canada - Labrador - west of 66°W	52.05	-67.81	55.34	-66
NAD_1927_MTQ_Lambert	3797	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1927_New_Brunswick_ Stereographic	5588	Canada - New Brunswick	44.56	-69.05	48.07	-63.7
NAD_1927_Quebec_Lambert	32098	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1927_StatePlane_Alabama_East_ FIPS_0101	26729	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1927_StatePlane_Alabama_West_ FIPS_0102	26730	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1927_StatePlane_Alaska_10_FIPS_ 5010	26740	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1927_StatePlane_Alaska_1_FIPS_ 5001	26731	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1927_StatePlane_Alaska_2_FIPS_ 5002	26732	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1927_StatePlane_Alaska_3_FIPS_ 5003	26733	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1927_StatePlane_Alaska_4_FIPS_ 5004	26734	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1927_StatePlane_Alaska_5_FIPS_ 5005	26735	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1927_StatePlane_Alaska_6_FIPS_ 5006	26736	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1927_StatePlane_Alaska_7_FIPS_ 5007	26737	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1927_StatePlane_Alaska_8_FIPS_ 5008	26738	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1927_StatePlane_Alaska_9_FIPS_ 5009	26739	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1927_StatePlane_Arizona_Central_ FIPS_0202	26749	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1927_StatePlane_Arizona_East_ FIPS_0201	26748	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1927_StatePlane_Arizona_West_ FIPS_0203	26750	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1927_StatePlane_Arkansas_North_ FIPS_0301	26751	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1927_StatePlane_Arkansas_South_ FIPS_0302	26752	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1927_StatePlane_California_I_FIPS_ 0401	26741	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1927_StatePlane_California_II_FIPS _0402	26742	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1927_StatePlane_California_III_FIPS _0403	26743	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1927_StatePlane_California_IV_FIPS _0404	26744	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1927_StatePlane_California_V_FIPS _0405	26745	USA - California - SPCS27 - 5	32.76	-121.43	35.81	-114.12
NAD_1927_StatePlane_California_VI_FIPS _0406	26746	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1927_StatePlane_California_VII_ FIPS_0407	26799	USA - California - SPCS27 - 7	33.66	-118.96	34.83	-117.63
NAD_1927_StatePlane_California_V_ Ventura	102699	USA - California - SPCS27 - 5	32.76	-121.43	35.81	-114.12
NAD_1927_StatePlane_Colorado_Central _FIPS_0502	26754	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1927_StatePlane_Colorado_North_ FIPS_0501	26753	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1927_StatePlane_Colorado_South_ FIPS_0503	26755	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1927_StatePlane_Connecticut_FIPS _0600	26756	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1927_StatePlane_Delaware_FIPS_ 0700	26757	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1927_StatePlane_Florida_East_FIPS _0901	26758	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1927_StatePlane_Florida_North_ FIPS_0903	26760	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1927_StatePlane_Florida_West_ FIPS_0902	26759	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1927_StatePlane_Georgia_East_ FIPS_1001	26766	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1927_StatePlane_Georgia_West_ FIPS_1002	26767	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1927_StatePlane_Guam_FIPS_5400	65061	Guam	10.95	141.19	15.91	148.18
NAD_1927_StatePlane_Idaho_Central_ FIPS_1102	26769	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1927_StatePlane_Idaho_East_FIPS_ 1101	26768	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1927_StatePlane_Idaho_West_FIPS _1103	26770	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1927_StatePlane_Illinois_East_FIPS _1201	26771	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1927_StatePlane_Illinois_West_FIPS _1202	26772	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1927_StatePlane_Indiana_East_FIPS _1301	26773	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1927_StatePlane_Indiana_West_ FIPS_1302	26774	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1927_StatePlane_Iowa_North_FIPS _1401	26775	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1927_StatePlane_Iowa_South_FIPS _1402	26776	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1927_StatePlane_Kansas_North_ FIPS_1501	26777	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1927_StatePlane_Kansas_South_ FIPS_1502	26778	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1927_StatePlane_Kentucky_North_ FIPS_1601	26779	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1927_StatePlane_Kentucky_South_ FIPS_1602	26780	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1927_StatePlane_Louisiana_North_ FIPS_1701	26781	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1927_StatePlane_Louisiana_ Offshore_FIPS_1703	32099	USA - Louisiana	28.85	-94.05	33.03	-88.75
NAD_1927_StatePlane_Louisiana_South_ FIPS_1702	26782	USA - Louisiana - SPCS27 - S	27.82	-93.94	31.07	-87.76
NAD_1927_StatePlane_Maine_East_FIPS _1801	26783	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1927_StatePlane_Maine_West_FIPS _1802	26784	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1927_StatePlane_Maryland_FIPS_ 1900	26785	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1927_StatePlane_Massachusetts_ Island_FIPS_2002	26787	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1927_StatePlane_Massachusetts_ Mainland_FIPS_2001	26786	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1927_StatePlane_Michigan_Central _FIPS_2112	26789	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1927_StatePlane_Michigan_Central _Old_FIPS_2102	5624	USA - Michigan - SPCS - old central	41.75	-87.61	46.11	-84.6
NAD_1927_StatePlane_Michigan_East_ Old_FIPS_2101	5623	USA - Michigan - SPCS - E	41.69	-84.87	46.04	-82.13
NAD_1927_StatePlane_Michigan_North_ FIPS_2111	26788	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1927_StatePlane_Michigan_South_ FIPS_2113	26790	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1927_StatePlane_Michigan_West_ Old_FIPS_2103	5625	USA - Michigan - SPCS - W	45.09	-90.42	48.32	-83.44
NAD_1927_StatePlane_Minnesota_ Central_FIPS_2202	26792	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1927_StatePlane_Minnesota_North _FIPS_2201	26791	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1927_StatePlane_Minnesota_South _FIPS_2203	26793	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1927_StatePlane_Mississippi_East_ FIPS_2301	26794	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1927_StatePlane_Mississippi_West _FIPS_2302	26795	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1927_StatePlane_Missouri_Central _FIPS_2402	26797	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1927_StatePlane_Missouri_East_ FIPS_2401	26796	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1927_StatePlane_Missouri_West_ FIPS_2403	26798	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1927_StatePlane_Montana_Central _FIPS_2502	32002	USA - Montana - SPCS27 - C	46.17	-116.06	48.26	-104.04
NAD_1927_StatePlane_Montana_North_ FIPS_2501	32001	USA - Montana - SPCS27 - N	47.41	-116.07	49.01	-104.04
NAD_1927_StatePlane_Montana_South_ FIPS_2503	32003	USA - Montana - SPCS27 - S	44.35	-114.57	46.87	-104.04
NAD_1927_StatePlane_Nebraska_North_ FIPS_2601	32005	USA - Nebraska - SPCS27 - N	41.68	-104.06	43.01	-96.07
NAD_1927_StatePlane_Nebraska_South_ FIPS_2602	32006	USA - Nebraska - SPCS27 - S	39.99	-104.06	42.01	-95.3
NAD_1927_StatePlane_Nevada_Central_ FIPS_2702	32008	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1927_StatePlane_Nevada_East_ FIPS_2701	32007	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1927_StatePlane_Nevada_West_ FIPS_2703	32009	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1927_StatePlane_New_Hampshire_ FIPS_2800	32010	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1927_StatePlane_New_Jersey_FIPS _2900	32011	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1927_StatePlane_New_Mexico_ Central_FIPS_3002	32013	USA - New Mexico - SPCS27 - C	31.78	-107.73	37	-104.83
NAD_1927_StatePlane_New_Mexico_ East_FIPS_3001	32012	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1927_StatePlane_New_Mexico_ West_FIPS_3003	32014	USA - New Mexico - SPCS27 - W	31.33	-109.06	37	-106.32
NAD_1927_StatePlane_New_York_ Central_FIPS_3102	32016	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1927_StatePlane_New_York_East_ FIPS_3101	32015	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1927_StatePlane_New_York_Long_ Island_FIPS_3104	4456	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1927_StatePlane_New_York_West_ FIPS_3103	32017	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1927_StatePlane_North_Carolina_ FIPS_3200	32019	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1927_StatePlane_North_Dakota_ North_FIPS_3301	32020	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1927_StatePlane_North_Dakota_ South_FIPS_3302	32021	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1927_StatePlane_Ohio_North_FIPS _3401	32022	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1927_StatePlane_Ohio_South_FIPS _3402	32023	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1927_StatePlane_Oklahoma_North _FIPS_3501	32024	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1927_StatePlane_Oklahoma_South _FIPS_3502	32025	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1927_StatePlane_Oregon_North_ FIPS_3601	32026	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1927_StatePlane_Oregon_South_ FIPS_3602	32027	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1927_StatePlane_Pennsylvania_ North_FIPS_3701	32028	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1927_StatePlane_Pennsylvania_ South_FIPS_3702	4455	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1927_StatePlane_Puerto_Rico_FIPS _5201	32059	Puerto Rico	14.92	-68.49	21.86	-65.04
NAD_1927_StatePlane_Rhode_Island_ FIPS_3800	32030	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1927_StatePlane_South_Carolina_ North_FIPS_3901	32031	USA - South Carolina - SPCS27 - N	33.46	-83.36	35.21	-78.52
NAD_1927_StatePlane_South_Carolina_ South_FIPS_3902	32033	USA - South Carolina - SPCS27 - S	32.05	-82.03	33.95	-78.95
NAD_1927_StatePlane_South_Dakota_ North_FIPS_4001	32034	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1927_StatePlane_South_Dakota_ South_FIPS_4002	32035	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1927_StatePlane_Tennessee_FIPS_ 4100	2204	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1927_StatePlane_Texas_Central_ FIPS_4203	32039	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1927_StatePlane_Texas_North_ Central_FIPS_4202	32038	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1927_StatePlane_Texas_North_FIPS _4201	32037	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1927_StatePlane_Texas_South_ Central_FIPS_4204	32040	USA - Texas - SPCS27 - SC	27.78	-105	30.67	-93.41
NAD_1927_StatePlane_Texas_South_FIPS _4205	32041	USA - Texas - SPCS27 - S	25.83	-100.2	28.21	-95.37
NAD_1927_StatePlane_Utah_Central_ FIPS_4302	32043	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1927_StatePlane_Utah_North_FIPS _4301	32042	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1927_StatePlane_Utah_South_FIPS _4303	32044	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1927_StatePlane_Vermont_FIPS_ 4400	32045	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1927_StatePlane_Virginia_North_ FIPS_4501	32046	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1927_StatePlane_Virginia_South_ FIPS_4502	32047	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1927_StatePlane_Virgin_Islands_ St_Croix_FIPS_5202	32060	Virgin Islands, US	16.22	-66.05	21.83	-63.88
NAD_1927_StatePlane_Washington_ North_FIPS_4601	32048	USA - Washington - SPCS27 - N	47.08	-124.79	49.05	-117.02
NAD_1927_StatePlane_Washington_ South_FIPS_4602	32049	USA - Washington - SPCS27 - S	45.54	-124.4	47.96	-116.91
NAD_1927_StatePlane_West_Virginia_ North_FIPS_4701	32050	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1927_StatePlane_West_Virginia_ South_FIPS_4702	32051	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1927_StatePlane_Wisconsin_Centra l_FIPS_4802	32053	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1927_StatePlane_Wisconsin_North _FIPS_4801	32052	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1927_StatePlane_Wisconsin_South _FIPS_4803	32054	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1927_StatePlane_Wyoming_East_ Central_FIPS_4902	32056	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1927_StatePlane_Wyoming_East_ FIPS_4901	32055	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1927_StatePlane_Wyoming_West_ Central_FIPS_4903	32057	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1927_StatePlane_Wyoming_West_ FIPS_4904	32058	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1927_Texas_Statewide_Mapping_ System	3080	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1927_UTM_Zone_10N	26710	North America - 126°W to 120°W and NAD27 by country - onshore	34.4	-126	77.13	-120
NAD_1927_UTM_Zone_11N	26711	North America - 120°W to 114°W and NAD27 by country - onshore	26.93	-120	78.13	-114
NAD_1927_UTM_Zone_12N	26712	North America - 114°W to 108°W and NAD27 by country	18.66	-114	78.81	-108
NAD_1927_UTM_Zone_13N	26713	North America - 108°W to 102°W and NAD27 by country	17.86	-108	79.42	-102
NAD_1927_UTM_Zone_14N	26714	North America - 102°W to 96°W and NAD27 by country	15.59	-102	80.74	-96
NAD_1927_UTM_Zone_15N	26715	North America - 96°W to 90°W and NAD27 by country	13.63	-96	81.96	-90
NAD_1927_UTM_Zone_16N	26716	North America - 90°W to 84°W and NAD27 by country	9.27	-90.01	82.54	-84
NAD_1927_UTM_Zone_17N	26717	North America - 84°W to 78°W and NAD27 by country	7.98	-84	83.03	-78
NAD_1927_UTM_Zone_18N	26718	North America - 78°W to 72°W and NAD27 by country	18.83	-78	83.16	-72
NAD_1927_UTM_Zone_19N	26719	North America - 72°W to 66°W and NAD27 by country	33.61	-72	83.17	-66
NAD_1927_UTM_Zone_1N	26701	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1927_UTM_Zone_20N	26720	North America - 66°W to 60°W and NAD27 by country	38.21	-66	82.97	-60
NAD_1927_UTM_Zone_21N	26721	Canada - 60°W to 54°W and NAD27	40.57	-60	68.93	-54
NAD_1927_UTM_Zone_22N	26722	Canada - 54°W to 48°W	39.5	-54	57.65	-48
NAD_1927_UTM_Zone_2N	26702	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1927_UTM_Zone_3N	26703	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1927_UTM_Zone_4N	26704	USA - 162°W to 156°W - AK, OCS	50.98	-162	74.71	-155.99
NAD_1927_UTM_Zone_59N	3370	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1927_UTM_Zone_5N	26705	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1927_UTM_Zone_60N	3371	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1927_UTM_Zone_6N	26706	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1927_UTM_Zone_7N	26707	North America - 144°W to 138°W and NAD27 by country	53.47	-144	73.59	-138
NAD_1927_UTM_Zone_8N	26708	North America - 138°W to 132°W and NAD27 by country - onshore	52.58	-138	73.04	-132
NAD_1927_UTM_Zone_9N	26709	North America - 132°W to 126°W and NAD27 by country - onshore	49.18	-132	72.03	-126
NAD_1927_Wisconsin_TM	3069	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_10TM_AEP_Forest	3400	Canada - Alberta	48.99	-120	60	-109.98
NAD_1983_10TM_AEP_Resource	3401	Canada - Alberta	48.99	-120	60	-109.98
NAD_1983_2011_Alaska_Albers	6393	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1983_2011_California_Teale_Albers	6414	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_2011_Contiguous_USA_ Albers	6350	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
NAD_1983_2011_EPSG_Arctic_zone_5-29	6351	Arctic - 74°30'N to 69°30'N, 173°W to 153°W	69.5	-173	74.51	-153
NAD_1983_2011_EPSG_Arctic_zone_5-31	6352	Arctic - 74°30'N to 69°30'N, 157°W to 137°W	69.5	-157	74.51	-137
NAD_1983_2011_EPSG_Arctic_zone_6-14	6353	Arctic - 71°10'N to 66°10'N, 174°W to 156°W	66.16	-174	71.17	-156
NAD_1983_2011_EPSG_Arctic_zone_6-16	6354	Arctic - 71°10'N to 66°10'N, 156°W to 138°W	66.16	-156	71.17	-138
NAD_1983_2011_Fargo_Ground_ Coordinate_System	102391	USA - North Dakota - Fargo	46.7	-96.93	47	-96.75
NAD_1983_2011_Florida_GDL_Albers	6439	USA - Florida	24.41	-87.63	31.01	-79.97
NAD_1983_(2011)_IaRCS_zone_1	7057	USA - Iowa - Spencer	42.9	-96.6	43.51	-93.97
NAD_1983_(2011)_IaRCS_zone_10	7066	USA - Iowa - Cedar Rapids	41.42	-92.31	42.3	-90.89
NAD_1983_(2011)_IaRCS_zone_11	7067	USA - Iowa - Dubuque- Davenport	41.44	-91.14	42.68	-90.14
NAD_1983_(2011)_IaRCS_zone_12	7068	USA - Iowa - Red Oak- Ottumwa	40.57	-95.39	41.17	-92.17
NAD_1983_(2011)_IaRCS_zone_13	7069	USA - Iowa - Fairfield	40.59	-92.42	41.52	-91.48
NAD_1983_(2011)_IaRCS_zone_14	7070	USA - Iowa - Burlington	40.37	-91.72	41.6	-90.78
NAD_1983_(2011)_IaRCS_zone_2	7058	USA - Iowa - Mason City	42.9	-93.98	43.51	-91.6
NAD_1983_(2011)_IaRCS_zone_3	7059	USA - Iowa - Elkader	42.29	-91.62	43.51	-90.89
NAD_1983_(2011)_IaRCS_zone_4	7060	USA - Iowa - Sioux City- Iowa Falls	42.2	-96.65	42.92	-93
NAD_1983_(2011)_IaRCS_zone_5	7061	USA - Iowa - Waterloo	42.2	-93.03	43.09	-91.59
NAD_1983_(2011)_IaRCS_zone_6	7062	USA - Iowa - Council Bluffs	40.58	-96.37	42.22	-95.04
NAD_1983_(2011)_IaRCS_zone_7	7063	USA - Iowa - Carroll- Atlantic	41.15	-95.16	42.22	-94.16
NAD_1983_(2011)_IaRCS_zone_8	7064	USA - Iowa - Ames-Des Moines	41.15	-94.29	42.22	-93.23
NAD_1983_(2011)_IaRCS_zone_9	7065	USA - Iowa - Newton	41.16	-93.35	42.3	-92.29
NAD_1983_(2011)_ICS_Aurora_ (US_Feet)	102901	Illinois - Aurora	41.45	-88.95	42.5	-88.19
NAD_1983_(2011)_ICS_Belleville_ (US_Feet)	102929	Illinois - Belleville	38.08	-90.38	39.01	-89.59
NAD_1983_(2011)_ICS_Bloomington_ (US_Feet)	102914	Illinois - Bloomington	40.28	-89.27	40.76	-88.45
NAD_1983_(2011)_ICS_Carbondale_ (US_Feet)	102932	Illinois - Carbondale	37.56	-90.21	38.26	-87.91
NAD_1983_(2011)_ICS_Carlinville_ (US_Feet)	102925	Illinois - Carlinville	38.99	-90.63	39.53	-89.69
NAD_1983_(2011)_ICS_Champaign_ (US_Feet)	102916	Illinois - Champaign	39.86	-88.47	40.5	-87.52
NAD_1983_(2011)_ICS_Charleston_ (US_Feet)	102924	Illinois - Charleston	39.37	-88.48	39.89	-87.53
NAD_1983_(2011)_ICS_Chicago_ (US_Feet)	102903	Illinois - Chicago	41.46	-88.27	42.5	-87.52
NAD_1983_(2011)_ICS_Decatur_ (US_Feet)	102917	Illinois - Decatur	39.21	-89.22	40.29	-88.46
NAD_1983_(2011)_ICS_Effingham_ (US_Feet)	102928	Illinois - Effingham	38.73	-89.64	39.22	-88.36
NAD_1983_(2011)_ICS_Eureka_ (US_Feet)	102909	Illinois - Eureka	40.59	-89.64	41.15	-88.92
NAD_1983_(2011)_ICS_Freeport_ (US_Feet)	102902	Illinois - Freeport	41.92	-90.66	42.51	-89.39
NAD_1983_(2011)_ICS_Galesburg_ (US_Feet)	102915	Illinois - Galesburg	40.18	-90.46	41.24	-89.63
NAD_1983_(2011)_ICS_Jacksonville_ (US_Feet)	102922	Illinois - Jacksonville	39.39	-91.38	39.88	-89.92
NAD_1983_(2011)_ICS_Jerseyville_ (US_Feet)	102927	Illinois - Jerseyville	38.86	-90.94	39.41	-90.14
NAD_1983_(2011)_ICS_Joliet_ (US_Feet)	102908	Illinois - Joliet	40.99	-88.27	41.73	-87.52
NAD_1983_(2011)_ICS_Lincoln_ (US_Feet)	102919	Illinois - Lincoln	39.87	-90.59	40.44	-89.14
NAD_1983_(2011)_ICS_Macomb_ (US_Feet)	102920	Illinois - Macomb	39.83	-90.92	40.64	-90.18
NAD_1983_(2011)_ICS_Metropolis_ (US_Feet)	102933	Illinois - Metropolis	36.97	-89.53	37.61	-88.05
NAD_1983_(2011)_ICS_Moline_ (US_Feet)	102905	Illinois - Moline	41.32	-91.08	41.79	-90.15
NAD_1983_(2011)_ICS_Monmouth_ (US_Feet)	102911	Illinois - Monmouth	40.62	-91.19	41.34	-90.43
NAD_1983_(2011)_ICS_Mount_ Vernon_(US_Feet)	102931	Illinois - Mount Vernon	38.12	-89.71	38.83	-88.69
NAD_1983_(2011)_ICS_Olney_ (US_Feet)	102930	Illinois - Olney	38.23	-88.71	38.92	-87.49
NAD_1983_(2011)_ICS_Ottawa_ (US_Feet)	102906	Illinois - Ottawa	40.92	-89.87	41.64	-88.24
NAD_1983_(2011)_ICS_Peoria_ (US_Feet)	102913	Illinois - Peoria	40.31	-90.01	40.98	-89.26
NAD_1983_(2011)_ICS_Pontiac_ (US_Feet)	102910	Illinois - Pontiac	40.61	-88.94	41.12	-88.23
NAD_1983_(2011)_ICS_Quincy_ (US_Feet)	102918	Illinois - Quincy	39.75	-91.52	40.64	-90.9
NAD_1983_(2011)_ICS_Robinson_ (US_Feet)	102926	Illinois - Robinson	38.84	-88.48	39.49	-87.51
NAD_1983_(2011)_ICS_Rockford_ (US_Feet)	102904	Illinois - Rockford	41.58	-89.69	42.51	-88.93
NAD_1983_(2011)_ICS_Springfield_ (US_Feet)	102921	Illinois - Springfield	39.52	-90.01	39.98	-89.21
NAD_1983_(2011)_ICS_Sterling_ (US_Feet)	102907	Illinois - Sterling	41.14	-90.44	41.94	-89.62
NAD_1983_(2011)_ICS_Taylorville_ (US_Feet)	102923	Illinois - Taylorville	38.99	-89.71	39.83	-89.02
NAD_1983_(2011)_ICS_Watseka_ (US_Feet)	102912	Illinois - Watseka	40.39	-88.47	41.02	-87.52
NAD_1983_2011_InGCS_Adams_(ftUS)	7258	USA - Indiana - Adams	40.56	-85.08	40.93	-84.8
NAD_1983_2011_InGCS_Adams_(m)	7257	USA - Indiana - Adams	40.56	-85.08	40.93	-84.8
NAD_1983_2011_InGCS_Allen_(ftUS)	7260	USA - Indiana - Allen	40.91	-85.34	41.28	-84.8
NAD_1983_2011_InGCS_Allen_(m)	7259	USA - Indiana - Allen	40.91	-85.34	41.28	-84.8
NAD_1983_2011_InGCS_Bartholomew_ (ftUS)	7262	USA - Indiana - Bartholomew	39.03	-86.09	39.36	-85.68
NAD_1983_2011_InGCS_Bartholomew_ (m)	7261	USA - Indiana - Bartholomew	39.03	-86.09	39.36	-85.68
NAD_1983_2011_InGCS_Benton_(ftUS)	7264	USA - Indiana - Benton	40.47	-87.53	40.74	-87.09
NAD_1983_2011_InGCS_Benton_(m)	7263	USA - Indiana - Benton	40.47	-87.53	40.74	-87.09
NAD_1983_2011_InGCS_Blackford- Delaware_(ftUS)	7266	USA - Indiana - Blackford and Delaware	40.07	-85.58	40.57	-85.2
NAD_1983_2011_InGCS_Blackford- Delaware_(m)	7265	USA - Indiana - Blackford and Delaware	40.07	-85.58	40.57	-85.2
NAD_1983_2011_InGCS_Boone- Hendricks_(ftUS)	7268	USA - Indiana - Boone and Hendricks	39.6	-86.7	40.19	-86.24
NAD_1983_2011_InGCS_Boone- Hendricks_(m)	7267	USA - Indiana - Boone and Hendricks	39.6	-86.7	40.19	-86.24
NAD_1983_2011_InGCS_Brown_(ftUS)	7270	USA - Indiana - Brown	39.04	-86.39	39.35	-86.07
NAD_1983_2011_InGCS_Brown_(m)	7269	USA - Indiana - Brown	39.04	-86.39	39.35	-86.07
NAD_1983_2011_InGCS_Carroll_(ftUS)	7272	USA - Indiana - Carroll	40.43	-86.78	40.74	-86.37
NAD_1983_2011_InGCS_Carroll_(m)	7271	USA - Indiana - Carroll	40.43	-86.78	40.74	-86.37
NAD_1983_2011_InGCS_Cass_(ftUS)	7274	USA - Indiana - Cass	40.56	-86.59	40.92	-86.16
NAD_1983_2011_InGCS_Cass_(m)	7273	USA - Indiana - Cass	40.56	-86.59	40.92	-86.16
NAD_1983_2011_InGCS_Clark-Floyd- Scott_(ftUS)	7276	USA - Indiana - Clark, Floyd, Scott	38.17	-86.04	38.84	-85.41
NAD_1983_2011_InGCS_Clark-Floyd- Scott_(m)	7275	USA - Indiana - Clark, Floyd, Scott	38.17	-86.04	38.84	-85.41
NAD_1983_2011_InGCS_Clay_(ftUS)	7278	USA - Indiana - Clay	39.16	-87.25	39.61	-86.93
NAD_1983_2011_InGCS_Clay_(m)	7277	USA - Indiana - Clay	39.16	-87.25	39.61	-86.93
NAD_1983_2011_InGCS_Clinton_(ftUS)	7280	USA - Indiana - Clinton	40.17	-86.7	40.44	-86.24
NAD_1983_2011_InGCS_Clinton_(m)	7279	USA - Indiana - Clinton	40.17	-86.7	40.44	-86.24
NAD_1983_2011_InGCS_Crawford- Lawrence-Orange_(ftUS)	7282	USA - Indiana - Crawford, Lawrence, Orange	38.1	-86.69	39	-86.24
NAD_1983_2011_InGCS_Crawford- Lawrence-Orange_(m)	7281	USA - Indiana - Crawford, Lawrence, Orange	38.1	-86.69	39	-86.24
NAD_1983_2011_InGCS_Daviess- Greene_(ftUS)	7284	USA - Indiana - Daviess and Greene	38.49	-87.28	39.18	-86.68
NAD_1983_2011_InGCS_Daviess- Greene_(m)	7283	USA - Indiana - Daviess and Greene	38.49	-87.28	39.18	-86.68
NAD_1983_2011_InGCS_Dearborn-Ohio- Switzerland_(ftUS)	7286	USA - Indiana - Dearborn, Ohio, Switzerland	38.68	-85.21	39.31	-84.78
NAD_1983_2011_InGCS_Dearborn-Ohio- Switzerland_(m)	7285	USA - Indiana - Dearborn, Ohio, Switzerland	38.68	-85.21	39.31	-84.78
NAD_1983_2011_InGCS_Decatur- Rush_(ftUS)	7288	USA - Indiana - Decatur and Rush	39.13	-85.69	39.79	-85.29
NAD_1983_2011_InGCS_Decatur- Rush_(m)	7287	USA - Indiana - Decatur and Rush	39.13	-85.69	39.79	-85.29
NAD_1983_2011_InGCS_DeKalb_(ftUS)	7290	USA - Indiana - DeKalb	41.26	-85.2	41.54	-84.8
NAD_1983_2011_InGCS_DeKalb_(m)	7289	USA - Indiana - DeKalb	41.26	-85.2	41.54	-84.8
NAD_1983_2011_InGCS_Dubois- Martin_(ftUS)	7292	USA - Indiana - Dubois and Martin	38.2	-87.08	38.91	-86.67
NAD_1983_2011_InGCS_Dubois- Martin_(m)	7291	USA - Indiana - Dubois and Martin	38.2	-87.08	38.91	-86.67
NAD_1983_2011_InGCS_Elkhart- Kosciusko-Wabash_(ftUS)	7294	USA - Indiana - Elkhart, Kosciusko, Wabash	40.65	-86.08	41.77	-85.63
NAD_1983_2011_InGCS_Elkhart- Kosciusko-Wabash_(m)	7293	USA - Indiana - Elkhart, Kosciusko, Wabash	40.65	-86.08	41.77	-85.63
NAD_1983_2011_InGCS_Fayette- Franklin-Union_(ftUS)	7296	USA - Indiana - Fayette, Franklin, Union	39.26	-85.31	39.79	-84.81
NAD_1983_2011_InGCS_Fayette- Franklin-Union_(m)	7295	USA - Indiana - Fayette, Franklin, Union	39.26	-85.31	39.79	-84.81
NAD_1983_2011_InGCS_Fountain- Warren_(ftUS)	7298	USA - Indiana - Fountain and Warren	39.95	-87.54	40.48	-87.09
NAD_1983_2011_InGCS_Fountain- Warren_(m)	7297	USA - Indiana - Fountain and Warren	39.95	-87.54	40.48	-87.09
NAD_1983_2011_InGCS_Fulton-Marshall- St_Joseph_(ftUS)	7300	USA - Indiana - Fulton, Marshall, St Joseph	40.9	-86.53	41.77	-85.94
NAD_1983_2011_InGCS_Fulton-Marshall- St_Joseph_(m)	7299	USA - Indiana - Fulton, Marshall, St Joseph	40.9	-86.53	41.77	-85.94
NAD_1983_2011_InGCS_Gibson_(ftUS)	7302	USA - Indiana - Gibson	38.16	-87.98	38.54	-87.31
NAD_1983_2011_InGCS_Gibson_(m)	7301	USA - Indiana - Gibson	38.16	-87.98	38.54	-87.31
NAD_1983_2011_InGCS_Grant_(ftUS)	7304	USA - Indiana - Grant	40.37	-85.87	40.66	-85.44
NAD_1983_2011_InGCS_Grant_(m)	7303	USA - Indiana - Grant	40.37	-85.87	40.66	-85.44
NAD_1983_2011_InGCS_Hamilton- Tipton_(ftUS)	7306	USA - Indiana - Hamilton and Tipton	39.92	-86.25	40.41	-85.86
NAD_1983_2011_InGCS_Hamilton- Tipton_(m)	7305	USA - Indiana - Hamilton and Tipton	39.92	-86.25	40.41	-85.86
NAD_1983_2011_InGCS_Hancock- Madison_(ftUS)	7308	USA - Indiana - Hancock and Madison	39.69	-85.96	40.38	-85.57
NAD_1983_2011_InGCS_Hancock- Madison_(m)	7307	USA - Indiana - Hancock and Madison	39.69	-85.96	40.38	-85.57
NAD_1983_2011_InGCS_Harrison- Washington_(ftUS)	7310	USA - Indiana - Harrison and Washington	37.95	-86.33	38.79	-85.84
NAD_1983_2011_InGCS_Harrison- Washington_(m)	7309	USA - Indiana - Harrison and Washington	37.95	-86.33	38.79	-85.84
NAD_1983_2011_InGCS_Henry_(ftUS)	7312	USA - Indiana - Henry	39.78	-85.6	40.08	-85.2
NAD_1983_2011_InGCS_Henry_(m)	7311	USA - Indiana - Henry	39.78	-85.6	40.08	-85.2
NAD_1983_2011_InGCS_Howard- Miami_(ftUS)	7314	USA - Indiana - Howard and Miami	40.37	-86.38	41	-85.86
NAD_1983_2011_InGCS_Howard- Miami_(m)	7313	USA - Indiana - Howard and Miami	40.37	-86.38	41	-85.86
NAD_1983_2011_InGCS_Huntington- Whitley_(ftUS)	7316	USA - Indiana - Huntington and Whitley	40.65	-85.69	41.3	-85.3
NAD_1983_2011_InGCS_Huntington- Whitley_(m)	7315	USA - Indiana - Huntington and Whitley	40.65	-85.69	41.3	-85.3
NAD_1983_2011_InGCS_Jackson_(ftUS)	7318	USA - Indiana - Jackson	38.72	-86.32	39.08	-85.79
NAD_1983_2011_InGCS_Jackson_(m)	7317	USA - Indiana - Jackson	38.72	-86.32	39.08	-85.79
NAD_1983_2011_InGCS_Jasper- Porter_(ftUS)	7320	USA - Indiana - Jasper and Porter	40.73	-87.28	41.77	-86.92
NAD_1983_2011_InGCS_Jasper- Porter_(m)	7319	USA - Indiana - Jasper and Porter	40.73	-87.28	41.77	-86.92
NAD_1983_2011_InGCS_Jay_(ftUS)	7322	USA - Indiana - Jay	40.3	-85.22	40.58	-84.8
NAD_1983_2011_InGCS_Jay_(m)	7321	USA - Indiana - Jay	40.3	-85.22	40.58	-84.8
NAD_1983_2011_InGCS_Jefferson_(ftUS)	7324	USA - Indiana - Jefferson	38.58	-85.69	38.92	-85.2
NAD_1983_2011_InGCS_Jefferson_(m)	7323	USA - Indiana - Jefferson	38.58	-85.69	38.92	-85.2
NAD_1983_2011_InGCS_Jennings_(ftUS)	7326	USA - Indiana - Jennings	38.8	-85.8	39.2	-85.43
NAD_1983_2011_InGCS_Jennings_(m)	7325	USA - Indiana - Jennings	38.8	-85.8	39.2	-85.43
NAD_1983_2011_InGCS_Johnson- Marion_(ftUS)	7328	USA - Indiana - Johnson and Marion	39.34	-86.33	39.93	-85.93
NAD_1983_2011_InGCS_Johnson- Marion_(m)	7327	USA - Indiana - Johnson and Marion	39.34	-86.33	39.93	-85.93
NAD_1983_2011_InGCS_Knox_(ftUS)	7330	USA - Indiana - Knox	38.41	-87.75	38.91	-87.09
NAD_1983_2011_InGCS_Knox_(m)	7329	USA - Indiana - Knox	38.41	-87.75	38.91	-87.09
NAD_1983_2011_InGCS_LaGrange- Noble_(ftUS)	7332	USA - Indiana - LaGrange and Noble	41.26	-85.66	41.77	-85.19
NAD_1983_2011_InGCS_LaGrange- Noble_(m)	7331	USA - Indiana - LaGrange and Noble	41.26	-85.66	41.77	-85.19
NAD_1983_2011_InGCS_Lake- Newton_(ftUS)	7334	USA - Indiana - Lake and Newton	40.73	-87.53	41.77	-87.21
NAD_1983_2011_InGCS_Lake- Newton_(m)	7333	USA - Indiana - Lake and Newton	40.73	-87.53	41.77	-87.21
NAD_1983_2011_InGCS_LaPorte-Pulaski- Starke_(ftUS)	7336	USA - Indiana - LaPorte, Pulaski, Starke	40.9	-86.94	41.77	-86.46
NAD_1983_2011_InGCS_LaPorte-Pulaski- Starke_(m)	7335	USA - Indiana - LaPorte, Pulaski, Starke	40.9	-86.94	41.77	-86.46
NAD_1983_2011_InGCS_Monroe- Morgan_(ftUS)	7338	USA - Indiana - Monroe and Morgan	38.99	-86.69	39.64	-86.24
NAD_1983_2011_InGCS_Monroe- Morgan_(m)	7337	USA - Indiana - Monroe and Morgan	38.99	-86.69	39.64	-86.24
NAD_1983_2011_InGCS_Montgomery- Putnam_(ftUS)	7340	USA - Indiana - Montgomery and Putnam	39.47	-87.1	40.22	-86.64
NAD_1983_2011_InGCS_Montgomery- Putnam_(m)	7339	USA - Indiana - Montgomery and Putnam	39.47	-87.1	40.22	-86.64
NAD_1983_2011_InGCS_Owen_(ftUS)	7342	USA - Indiana - Owen	39.16	-87.06	39.48	-86.63
NAD_1983_2011_InGCS_Owen_(m)	7341	USA - Indiana - Owen	39.16	-87.06	39.48	-86.63
NAD_1983_2011_InGCS_Parke- Vermillion_(ftUS)	7344	USA - Indiana - Parke and Vermillion	39.6	-87.54	40.15	-87
NAD_1983_2011_InGCS_Parke- Vermillion_(m)	7343	USA - Indiana - Parke and Vermillion	39.6	-87.54	40.15	-87
NAD_1983_2011_InGCS_Perry_(ftUS)	7346	USA - Indiana - Perry	37.84	-86.82	38.27	-86.43
NAD_1983_2011_InGCS_Perry_(m)	7345	USA - Indiana - Perry	37.84	-86.82	38.27	-86.43
NAD_1983_2011_InGCS_Pike- Warrick_(ftUS)	7348	USA - Indiana - Pike and Warrick	37.87	-87.48	38.56	-87.01
NAD_1983_2011_InGCS_Pike- Warrick_(m)	7347	USA - Indiana - Pike and Warrick	37.87	-87.48	38.56	-87.01
NAD_1983_2011_InGCS_Posey_(ftUS)	7350	USA - Indiana - Posey	37.77	-88.06	38.24	-87.68
NAD_1983_2011_InGCS_Posey_(m)	7349	USA - Indiana - Posey	37.77	-88.06	38.24	-87.68
NAD_1983_2011_InGCS_Randolph- Wayne_(ftUS)	7352	USA - Indiana - Randolph and Wayne	39.71	-85.23	40.32	-84.8
NAD_1983_2011_InGCS_Randolph- Wayne_(m)	7351	USA - Indiana - Randolph and Wayne	39.71	-85.23	40.32	-84.8
NAD_1983_2011_InGCS_Ripley_(ftUS)	7354	USA - Indiana - Ripley	38.91	-85.45	39.32	-85.06
NAD_1983_2011_InGCS_Ripley_(m)	7353	USA - Indiana - Ripley	38.91	-85.45	39.32	-85.06
NAD_1983_2011_InGCS_Shelby_(ftUS)	7356	USA - Indiana - Shelby	39.34	-85.96	39.7	-85.62
NAD_1983_2011_InGCS_Shelby_(m)	7355	USA - Indiana - Shelby	39.34	-85.96	39.7	-85.62
NAD_1983_2011_InGCS_Spencer_(ftUS)	7358	USA - Indiana - Spencer	37.78	-87.27	38.21	-86.76
NAD_1983_2011_InGCS_Spencer_(m)	7357	USA - Indiana - Spencer	37.78	-87.27	38.21	-86.76
NAD_1983_2011_InGCS_Steuben_(ftUS)	7360	USA - Indiana - Steuben	41.52	-85.2	41.77	-84.8
NAD_1983_2011_InGCS_Steuben_(m)	7359	USA - Indiana - Steuben	41.52	-85.2	41.77	-84.8
NAD_1983_2011_InGCS_Sullivan_(ftUS)	7362	USA - Indiana - Sullivan	38.9	-87.65	39.26	-87.24
NAD_1983_2011_InGCS_Sullivan_(m)	7361	USA - Indiana - Sullivan	38.9	-87.65	39.26	-87.24
NAD_1983_2011_InGCS_Tippecanoe- White_(ftUS)	7364	USA - Indiana - Tippecanoe and White	40.21	-87.1	40.92	-86.58
NAD_1983_2011_InGCS_Tippecanoe- White_(m)	7363	USA - Indiana - Tippecanoe and White	40.21	-87.1	40.92	-86.58
NAD_1983_2011_InGCS_Vanderburgh_ (ftUS)	7366	USA - Indiana - Vanderburgh	37.82	-87.71	38.17	-87.44
NAD_1983_2011_InGCS_Vanderburgh_ (m)	7365	USA - Indiana - Vanderburgh	37.82	-87.71	38.17	-87.44
NAD_1983_2011_InGCS_Vigo_(ftUS)	7368	USA - Indiana - Vigo	39.25	-87.62	39.61	-87.19
NAD_1983_2011_InGCS_Vigo_(m)	7367	USA - Indiana - Vigo	39.25	-87.62	39.61	-87.19
NAD_1983_2011_InGCS_Wells_(ftUS)	7370	USA - Indiana - Wells	40.56	-85.45	40.92	-85.06
NAD_1983_2011_InGCS_Wells_(m)	7369	USA - Indiana - Wells	40.56	-85.45	40.92	-85.06
NAD_1983_2011_Kansas_LCC	6924	USA - Kansas	36.99	-102.06	40.01	-94.58
NAD_1983_2011_Kansas_LCC_ftUS	6925	USA - Kansas	36.98	-102.06	40.01	-94.58
NAD_1983_2011_KS_RCS_Zone_1	8518	USA - Kansas - Goodland	38.69	-102.06	40.01	-101.38
NAD_1983_2011_KS_RCS_Zone_2	8519	USA - Kansas - Colby	38.69	-101.49	40.01	-100.71
NAD_1983_2011_KS_RCS_Zone_3	8520	USA - Kansas - Oberlin	38.69	-100.82	40.01	-100.14
NAD_1983_2011_KS_RCS_Zone_4	8521	USA - Kansas - Hays	38.69	-100.19	40.01	-99.03
NAD_1983_2011_KS_RCS_Zone_5	8522	USA - Kansas - Great Bend	38.26	-99.07	40.01	-98.47
NAD_1983_2011_KS_RCS_Zone_6	8523	USA - Kansas - Beloit	38.15	-98.51	40.01	-97.92
NAD_1983_2011_KS_RCS_Zone_7	8524	USA - Kansas - Salina	38.08	-97.94	40.01	-96.8
NAD_1983_2011_KS_RCS_Zone_8	8525	USA - Kansas - Manhattan	38.73	-96.97	39.57	-95.94
NAD_1983_2011_KS_RCS_Zone_9	8526	USA - Kansas - Emporia	38.08	-96.94	38.88	-95.94
NAD_1983_2011_KS_RCS_Zone_10	8527	USA - Kansas - Atchison	39.21	-96.81	40.01	-94.85
NAD_1983_2011_KS_RCS_Zone_11	8528	USA - Kansas - Kansas City	38.73	-96.04	39.43	-94.58
NAD_1983_2011_KS_RCS_Zone_12	8529	USA - Kansas - Ulysses	36.99	-102.05	38.71	-101.06
NAD_1983_2011_KS_RCS_Zone_13	8531	USA - Kansas - Garden City	36.99	-101.13	38.71	-100.08
NAD_1983_2011_KS_RCS_Zone_14	8533	USA - Kansas - Dodge City	36.99	-100.25	38.7	-99.54
NAD_1983_2011_KS_RCS_Zone_15	8534	USA - Kansas - Larned	36.99	-99.59	38.7	-98.91
NAD_1983_2011_KS_RCS_Zone_16	8535	USA - Kansas - Pratt	36.99	-99.03	38.27	-98.34
NAD_1983_2011_KS_RCS_Zone_17	8536	USA - Kansas - Wichita	37.38	-98.48	38.18	-96.52
NAD_1983_2011_KS_RCS_Zone_18	8538	USA - Kansas - Arkansas City	36.99	-98.35	37.48	-96.52
NAD_1983_2011_KS_RCS_Zone_19	8539	USA - Kansas - Coffeyville	36.99	-96.53	38.88	-95.5
NAD_1983_2011_KS_RCS_Zone_20	8540	USA - Kansas - Pittsburg	36.99	-95.53	38.74	-94.6
NAD_1983_2011_Maine_2000_Central_ Zone	6480	USA - Maine - CS2000 - C	43.75	-70.03	47.47	-68.33
NAD_1983_2011_Maine_2000_East_ Zone	6481	USA - Maine - CS2000 - E	44.18	-68.58	47.37	-66.91
NAD_1983_2011_Maine_2000_West_ Zone	6482	USA - Maine - CS2000 - W	43.07	-71.09	46.58	-69.61
NAD_1983_2011_Michigan_GeoRef_ Meters	6497	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1983_2011_Mississippi_TM	6508	USA - Mississippi	30.01	-91.65	35.01	-88.09
NAD_1983_(2011)_Navajo_Nation_ Coordinate_System_Meters	103592	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_(2011)_Navajo_Nation_ Coordinate_System_US_Feet	103593	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_(2011)_Navajo_Nation_ Coordinate_System_Intl_Feet	103594	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_(2011)_NCRS_Las_Vegas_ (ftUS)	8384	USA - Nevada - Las Vegas	35.89	-115.5	36.43	-114.72
NAD_1983_(2011)_NCRS_Las_Vegas_high (ftUS)	8387	USA - Nevada - Las Vegas - high elevation	35.89	-115.5	36.43	-114.72
NAD_1983_(2011)_NCRS_Las_Vegas_high _(m)	8385	USA - Nevada - Las Vegas - high elevation	35.89	-115.5	36.43	-114.72
NAD_1983_(2011)_NCRS_Las_Vegas_(m)	8383	USA - Nevada - Las Vegas	35.89	-115.5	36.43	-114.72
NAD_1983_2011_Oregon_Statewide_ Lambert	6556	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_2011_Oregon_Statewide_ Lambert_Ft_Intl	6557	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_(2011)_PCCS_zone_1_(ft)	8065	USA - Arizona - Pima county east	31.43	-111.57	32.52	-110.44
NAD_1983_(2011)_PCCS_zone_2_(ft)	8066	USA - Arizona - Pima county central	31.5	-112.52	32.51	-111.56
NAD_1983_(2011)_PCCS_zone_3_(ft)	8067	USA - Arizona - Pima county west	31.8	-113.33	32.51	-112.51
NAD_1983_(2011)_PCCS_zone_4_(ft)	8068	USA - Arizona - Pima county Mt. Lemmon	32.33	-110.87	32.49	-110.61
NAD_1983_2011_RMTCRS_Billings_Ft_ Intl	7127	USA - Montana - Billings	44.99	-109.42	47.41	-107.99
NAD_1983_2011_RMTCRS_Billings_ Meters	7117	USA - Montana - Billings	44.99	-109.42	47.41	-107.99
NAD_1983_2011_RMTCRS_Blackfeet_Ft_ Intl	7120	USA - Montana - Blackfeet reservation	48	-113.84	49.01	-112
NAD_1983_2011_RMTCRS_Blackfeet_ Meters	7110	USA - Montana - Blackfeet reservation	48	-113.84	49.01	-112
NAD_1983_2011_RMTCRS_Bobcat_Ft_ Intl	7126	USA - Montana - Three Forks	45.36	-112.34	46.59	-110.75
NAD_1983_2011_RMTCRS_Bobcat_ Meters	7116	USA - Montana - Three Forks	45.36	-112.34	46.59	-110.75
NAD_1983_2011_RMTCRS_Crow_Ft_Intl	7125	USA - Montana - Crow reservation	44.99	-108.84	46.09	-106.66
NAD_1983_2011_RMTCRS_Crow_Meters	7115	USA - Montana - Crow reservation	44.99	-108.84	46.09	-106.66
NAD_1983_2011_RMTCRS_Fort_Belknap _Ft_Intl	7122	USA - Montana - Fort Belknap	47.78	-110.84	49.01	-106.99
NAD_1983_2011_RMTCRS_Fort_Belknap _Meters	7112	USA - Montana - Fort Belknap	47.78	-110.84	49.01	-106.99
NAD_1983_2011_RMTCRS_Fort_Peck_ Assiniboine_Ft_Intl	7123	USA - Montana - Fort Peck higher areas	48.01	-107.57	48.88	-104.78
NAD_1983_2011_RMTCRS_Fort_Peck_ Assiniboine_Meters	7113	USA - Montana - Fort Peck higher areas	48.01	-107.57	48.88	-104.78
NAD_1983_2011_RMTCRS_Fort_Peck_ Sioux_Ft_Intl	7124	USA - Montana - Fort Peck lower areas	47.75	-107.76	49.01	-104.04
NAD_1983_2011_RMTCRS_Fort_Peck_ Sioux_Meters	7114	USA - Montana - Fort Peck lower areas	47.75	-107.76	49.01	-104.04
NAD_1983_2011_RMTCRS_Milk_River_Ft _Intl	7121	USA - Montana - Milk River	47.78	-112.5	49.01	-108.74
NAD_1983_2011_RMTCRS_Milk_River_ Meters	7111	USA - Montana - Milk River	47.78	-112.5	49.01	-108.74
NAD_1983_2011_RMTCRS_St_Mary_Ft_ Intl	7119	USA - Montana - St Mary valley	48.55	-113.97	49.01	-113
NAD_1983_2011_RMTCRS_St_Mary_ Meters	7109	USA - Montana - St Mary valley	48.55	-113.97	49.01	-113
NAD_1983_2011_RMTCRS_Wind_River_ (ftUS)	7128	USA - Wyoming - Wind River reservation	42.69	-109.5	43.86	-107.94
NAD_1983_2011_RMTCRS_Wind_River_ Meters	7118	USA - Wyoming - Wind River reservation	42.69	-109.5	43.86	-107.94
NAD_1983_2011_San_Francisco_CS13_ ftUS	7132	USA - California - San Francisco Bay Area	36.85	-123.56	38.87	-121.2
NAD_1983_2011_San_Francisco_CS13_ Meters	7131	USA - California - San Francisco Bay Area	36.85	-123.56	38.87	-121.2

Projected Coordinate Systems Part Two

Name	WKID	Area of Use	Minimum Latitude	Minimum Longitude	Maximum Latitude	Maximum Longitude
NAD_1983_2011_StatePlane_Alabama_ East_FIPS_0101	6355	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_2011_StatePlane_Alabama_ West_FIPS_0102	6356	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_2011_StatePlane_Alabama_ East_(ftUS)	9748	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_2011_StatePlane_Alabama_ West_(ftUS)	9749	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_2011_StatePlane_Alaska_10_ FIPS_5010	6403	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_2011_StatePlane_Alaska_10_ FIPS_5010_Feet	102398	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_2011_StatePlane_Alaska_1_ FIPS_5001	6394	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_2011_StatePlane_Alaska_1_ FIPS_5001_Feet	102445	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_2011_StatePlane_Alaska_2_ FIPS_5002	6395	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_2011_StatePlane_Alaska_2_ FIPS_5002_Feet	102446	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_2011_StatePlane_Alaska_3_ FIPS_5003	6396	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_2011_StatePlane_Alaska_3_ FIPS_5003_Feet	102447	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_2011_StatePlane_Alaska_4_ FIPS_5004	6397	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_2011_StatePlane_Alaska_4_ FIPS_5004_Feet	102392	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_2011_StatePlane_Alaska_5_ FIPS_5005	6398	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_2011_StatePlane_Alaska_5_ FIPS_5005_Feet	102393	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_2011_StatePlane_Alaska_6_ FIPS_5006	6399	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_2011_StatePlane_Alaska_6_ FIPS_5006_Feet	102394	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_2011_StatePlane_Alaska_7_ FIPS_5007	6400	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_2011_StatePlane_Alaska_7_ FIPS_5007_Feet	102395	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_2011_StatePlane_Alaska_8_ FIPS_5008	6401	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_2011_StatePlane_Alaska_8_ FIPS_5008_Feet	102396	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_2011_StatePlane_Alaska_9_ FIPS_5009	6402	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_2011_StatePlane_Alaska_9_ FIPS_5009_Feet	102397	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_2011_StatePlane_Arizona_ Central_FIPS_0202	6404	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_2011_StatePlane_Arizona_ Central_FIPS_0202_Ft_Intl	6405	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_2011_StatePlane_Arizona_ East_FIPS_0201	6406	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_2011_StatePlane_Arizona_ East_FIPS_0201_Ft_Intl	6407	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_2011_StatePlane_Arizona_ West_FIPS_0203	6408	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_2011_StatePlane_Arizona_ West_FIPS_0203_Ft_Intl	6409	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_2011_StatePlane_Arkansas_ North_FIPS_0301	6410	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_2011_StatePlane_Arkansas_ North_FIPS_0301_Ft_US	6411	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_2011_StatePlane_Arkansas_ South_FIPS_0302	6412	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_2011_StatePlane_Arkansas_ South_FIPS_0302_Ft_US	6413	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_2011_StatePlane_California_ I_FIPS_0401	6415	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_2011_StatePlane_California_ I_FIPS_0401_Ft_US	6416	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_2011_StatePlane_California_II _FIPS_0402	6417	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_2011_StatePlane_California_II _FIPS_0402_Ft_US	6418	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_2011_StatePlane_California_ III_FIPS_0403	6419	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_2011_StatePlane_California_ III_FIPS_0403_Ft_US	6420	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_2011_StatePlane_California_ IV_FIPS_0404	6421	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_2011_StatePlane_California_ IV_FIPS_0404_Ft_US	6422	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_2011_StatePlane_California_ V_FIPS_0405	6423	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_2011_StatePlane_California_ V_FIPS_0405_Ft_US	6424	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_2011_StatePlane_California_ VI_FIPS_0406	6425	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_2011_StatePlane_California_ VI_FIPS_0406_Ft_US	6426	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_2011_StatePlane_Colorado_ Central_FIPS_0502	6427	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_2011_StatePlane_Colorado_ Central_FIPS_0502_Ft_US	6428	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_2011_StatePlane_Colorado_ North_FIPS_0501	6429	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_2011_StatePlane_Colorado_ North_FIPS_0501_Ft_US	6430	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_2011_StatePlane_Colorado_ South_FIPS_0503	6431	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_2011_StatePlane_Colorado_ South_FIPS_0503_Ft_US	6432	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_2011_StatePlane_Connecticut _FIPS_0600	6433	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_2011_StatePlane_Connecticut _FIPS_0600_Ft_US	6434	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_2011_StatePlane_Delaware_ FIPS_0700	6435	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_2011_StatePlane_Delaware_ FIPS_0700_Ft_US	6436	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_2011_StatePlane_Florida_ East_FIPS_0901	6437	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_2011_StatePlane_Florida_ East_FIPS_0901_Ft_US	6438	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_2011_StatePlane_Florida_ North_FIPS_0903	6440	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_2011_StatePlane_Florida_ North_FIPS_0903_Ft_US	6441	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_2011_StatePlane_Florida_ West_FIPS_0902	6442	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_2011_StatePlane_Florida_ West_FIPS_0902_Ft_US	6443	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_2011_StatePlane_Georgia_ East_FIPS_1001	6444	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_2011_StatePlane_Georgia_ East_FIPS_1001_Ft_US	6445	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_2011_StatePlane_Georgia_ West_FIPS_1002	6446	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_2011_StatePlane_Georgia_ West_FIPS_1002_Ft_US	6447	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_2011_StatePlane_Idaho_ Central_FIPS_1102	6448	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_2011_StatePlane_Idaho_ Central_FIPS_1102_Ft_US	6449	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_2011_StatePlane_Idaho_ East_FIPS_1101	6450	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_2011_StatePlane_Idaho_ East_FIPS_1101_Ft_US	6451	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_2011_StatePlane_Idaho_ West_FIPS_1103	6452	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_2011_StatePlane_Idaho_ West_FIPS_1103_Ft_US	6453	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_2011_StatePlane_Illinois_East _FIPS_1201	6454	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_2011_StatePlane_Illinois_East _FIPS_1201_Ft_US	6455	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_2011_StatePlane_Illinois_ West_FIPS_1202	6456	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_2011_StatePlane_Illinois_ West_FIPS_1202_Ft_US	6457	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_2011_StatePlane_Indiana_ East_FIPS_1301	6458	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_2011_StatePlane_Indiana_ East_FIPS_1301_Ft_US	6459	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_2011_StatePlane_Indiana_ West_FIPS_1302	6460	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_2011_StatePlane_Indiana_ West_FIPS_1302_Ft_US	6461	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_2011_StatePlane_Iowa_North _FIPS_1401	6462	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_2011_StatePlane_Iowa_North _FIPS_1401_Ft_US	6463	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_2011_StatePlane_Iowa_South _FIPS_1402	6464	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_2011_StatePlane_Iowa_South _FIPS_1402_Ft_US	6465	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_2011_StatePlane_Kansas_ North_FIPS_1501	6466	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_2011_StatePlane_Kansas_ North_FIPS_1501_Ft_US	6467	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_2011_StatePlane_Kansas_ South_FIPS_1502	6468	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_2011_StatePlane_Kansas_ South_FIPS_1502_Ft_US	6469	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_2011_StatePlane_Kentucky_ FIPS_1600	6472	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_2011_StatePlane_Kentucky_ FIPS_1600_Ft_US	6473	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_2011_StatePlane_Kentucky_ North_FIPS_1601	6470	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_2011_StatePlane_Kentucky_ North_FIPS_1601_Ft_US	6471	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_2011_StatePlane_Kentucky_ South_FIPS_1602	6474	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_2011_StatePlane_Kentucky_ South_FIPS_1602_Ft_US	6475	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_2011_StatePlane_Louisiana_ North_FIPS_1701	6476	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_2011_StatePlane_Louisiana_ North_FIPS_1701_Ft_US	6477	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_2011_StatePlane_Louisiana_ South_FIPS_1702	6478	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_2011_StatePlane_Louisiana_ South_FIPS_1702_Ft_US	6479	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_2011_StatePlane_Maine_East _FIPS_1801	6483	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_2011_StatePlane_Maine_East _FIPS_1801_Ft_US	6484	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_2011_StatePlane_Maine_ West_FIPS_1802	6485	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_2011_StatePlane_Maine_ West_FIPS_1802_Ft_US	6486	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_2011_StatePlane_Maryland_ FIPS_1900	6487	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_2011_StatePlane_Maryland_ FIPS_1900_Ft_US	6488	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_2011_StatePlane_ Massachusetts_Island_FIPS_2002	6489	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_2011_StatePlane_ Massachusetts_Isl_FIPS_2002_FtUS	6490	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_2011_StatePlane_ Massachusetts_Mainland_FIPS_2001	6491	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_2011_StatePlane_ Massachusetts_Mnld_FIPS_2001_FtUS	6492	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_2011_StatePlane_Michigan_ Central_FIPS_2112	6493	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_2011_StatePlane_Michigan_ Central_FIPS_2112_Ft_Intl	6494	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_2011_StatePlane_Michigan_ North_FIPS_2111	6495	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_2011_StatePlane_Michigan_ North_FIPS_2111_Ft_Intl	6496	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_2011_StatePlane_Michigan_ South_FIPS_2113	6498	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_2011_StatePlane_Michigan_ South_FIPS_2113_Ft_Intl	6499	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_2011_StatePlane_Minnesota_ Central_FIPS_2202	6500	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_2011_StatePlane_Minnesota_ Central_FIPS_2202_Ft_US	6501	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_2011_StatePlane_Minnesota_ North_FIPS_2201	6502	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_2011_StatePlane_Minnesota_ North_FIPS_2201_Ft_US	6503	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_2011_StatePlane_Minnesota_ South_FIPS_2203	6504	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_2011_StatePlane_Minnesota_ South_FIPS_2203_Ft_US	6505	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_2011_StatePlane_Mississippi_ East_FIPS_2301	6506	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_2011_StatePlane_Mississippi_ East_FIPS_2301_Ft_US	6507	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_2011_StatePlane_Mississippi_ West_FIPS_2302	6509	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_2011_StatePlane_Mississippi_ West_FIPS_2302_Ft_US	6510	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_2011_StatePlane_Missouri_ Central_FIPS_2402	6511	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_2011_StatePlane_Missouri_ East_FIPS_2401	6512	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_2011_StatePlane_Missouri_ West_FIPS_2403	6513	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_2011_StatePlane_Montana_ FIPS_2500	6514	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_2011_StatePlane_Montana_ FIPS_2500_Ft_Intl	6515	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_2011_StatePlane_Nebraska_ FIPS_2600	6516	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_2011_StatePlane_Nebraska_ FIPS_2600_Ft_US	6880	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_2011_StatePlane_Nevada_ Central_FIPS_2702	6518	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_2011_StatePlane_Nevada_ Central_FIPS_2702_Ft_US	6519	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_2011_StatePlane_Nevada_ East_FIPS_2701	6520	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_2011_StatePlane_Nevada_ East_FIPS_2701_Ft_US	6521	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_2011_StatePlane_Nevada_ West_FIPS_2703	6522	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_2011_StatePlane_Nevada_ West_FIPS_2703_Ft_US	6523	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_2011_StatePlane_New_ Hampshire_FIPS_2800	6524	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_2011_StatePlane_New_ Hampshire_FIPS_2800_Ft_US	6525	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_2011_StatePlane_New_Jersey _FIPS_2900	6526	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_2011_StatePlane_New_Jersey _FIPS_2900_Ft_US	6527	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_2011_StatePlane_New_ Mexico_Central_FIPS_3002	6528	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_2011_StatePlane_New_ Mexico_Central_FIPS_3002_Ft_US	6529	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_2011_StatePlane_New_ Mexico_East_FIPS_3001	6530	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_2011_StatePlane_New_ Mexico_East_FIPS_3001_Ft_US	6531	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_2011_StatePlane_New_ Mexico_West_FIPS_3003	6532	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_2011_StatePlane_New_ Mexico_West_FIPS_3003_Ft_US	6533	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_2011_StatePlane_New_York_ Central_FIPS_3102	6534	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_2011_StatePlane_New_York_ Central_FIPS_3102_Ft_US	6535	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_2011_StatePlane_New_York_ East_FIPS_3101	6536	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_2011_StatePlane_New_York_ East_FIPS_3101_Ft_US	6537	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_2011_StatePlane_New_York_ Long_Island_FIPS_3104	6538	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_2011_StatePlane_New_York_ Long_Isl_FIPS_3104_Ft_US	6539	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_2011_StatePlane_New_York_ West_FIPS_3103	6540	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_2011_StatePlane_New_York_ West_FIPS_3103_Ft_US	6541	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_2011_StatePlane_North_ Carolina_FIPS_3200	6542	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_2011_StatePlane_North_ Carolina_FIPS_3200_Ft_US	6543	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_2011_StatePlane_North_ Dakota_North_FIPS_3301	6544	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_2011_StatePlane_North_ Dakota_North_FIPS_3301_FtI	6545	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_2011_StatePlane_North_ Dakota_South_FIPS_3302	6546	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_2011_StatePlane_North_ Dakota_South_FIPS_3302_FtI	6547	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_2011_StatePlane_Ohio_North _FIPS_3401	6548	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_2011_StatePlane_Ohio_North _FIPS_3401_Ft_US	6549	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_2011_StatePlane_Ohio_South _FIPS_3402	6550	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_2011_StatePlane_Ohio_South _FIPS_3402_Ft_US	6551	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_2011_StatePlane_Oklahoma_ North_FIPS_3501	6552	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_2011_StatePlane_Oklahoma_ North_FIPS_3501_Ft_US	6553	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_2011_StatePlane_Oklahoma_ South_FIPS_3502	6554	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_2011_StatePlane_Oklahoma_ South_FIPS_3502_Ft_US	6555	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_2011_StatePlane_Oregon_ North_FIPS_3601	6558	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_2011_StatePlane_Oregon_ North_FIPS_3601_Ft_Intl	6559	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_2011_StatePlane_Oregon_ South_FIPS_3602	6560	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_2011_StatePlane_Oregon_ South_FIPS_3602_Ft_Intl	6561	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_2011_StatePlane_ Pennsylvania_North_FIPS_3701	6562	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_2011_StatePlane_ Pennsylvania_North_FIPS_3701_Ft_US	6563	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_2011_StatePlane_ Pennsylvania_South_FIPS_3702	6564	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_2011_StatePlane_ Pennsylvania_South_FIPS_3702_Ft_US	6565	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_2011_StatePlane_Puerto_ Rico_Virgin_Isls_FIPS_5200	6566	Caribbean - Puerto Rico and US Virgin Islands - onshore	17.62	-67.97	18.57	-64.51
NAD_1983_2011_StatePlane_Rhode_ Island_FIPS_3800	6567	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_2011_StatePlane_Rhode_ Island_FIPS_3800_Ft_US	6568	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_2011_StatePlane_South_ Carolina_FIPS_3900	6569	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_2011_StatePlane_South_ Carolina_FIPS_3900_Ft_Intl	6570	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_2011_StatePlane_South_ Dakota_North_FIPS_4001	6571	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_2011_StatePlane_South_ Dakota_North_FIPS_4001_Ft_US	6572	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_2011_StatePlane_South_ Dakota_South_FIPS_4002	6573	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_2011_StatePlane_South_ Dakota_South_FIPS_4002_Ft_US	6574	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_2011_StatePlane_Tennessee_ FIPS_4100	6575	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_2011_StatePlane_Tennessee_ FIPS_4100_Ft_US	6576	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_2011_StatePlane_Texas_ Central_FIPS_4203	6577	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_2011_StatePlane_Texas_ Central_FIPS_4203_Ft_US	6578	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_2011_StatePlane_Texas_ North_Central_FIPS_4202	6583	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_2011_StatePlane_Texas_ North_Central_FIPS_4202_FtUS	6584	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_2011_StatePlane_Texas_ North_FIPS_4201	6581	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_2011_StatePlane_Texas_ North_FIPS_4201_Ft_US	6582	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_2011_StatePlane_Texas_ South_Central_FIPS_4204	6587	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_2011_StatePlane_Texas_ South_Central_FIPS_4204_FtUS	6588	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_2011_StatePlane_Texas_ South_FIPS_4205	6585	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_2011_StatePlane_Texas_ South_FIPS_4205_Ft_US	6586	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_2011_StatePlane_Utah_ Central_FIPS_4302	6619	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_2011_StatePlane_Utah_ Central_FIPS_4302_Ft_Intl	103167	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_2011_StatePlane_Utah_ Central_FIPS_4302_Ft_US	6625	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_2011_StatePlane_Utah_North _FIPS_4301	6620	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_2011_StatePlane_Utah_North _FIPS_4301_Ft_Intl	103166	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_2011_StatePlane_Utah_North _FIPS_4301_Ft_US	6626	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_2011_StatePlane_Utah_South _FIPS_4303	6621	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_2011_StatePlane_Utah_South _FIPS_4303_Ft_Intl	103168	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_2011_StatePlane_Utah_South _FIPS_4303_Ft_US	6627	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_2011_StatePlane_Vermont_ FIPS_4400	6589	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_2011_StatePlane_Vermont_ FIPS_4400_Ft_US	6590	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_2011_StatePlane_Virginia_ North_FIPS_4501	6592	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_2011_StatePlane_Virginia_ North_FIPS_4501_Ft_US	6593	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_2011_StatePlane_Virginia_ South_FIPS_4502	6594	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_2011_StatePlane_Virginia_ South_FIPS_4502_Ft_US	6595	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_2011_StatePlane_Washington _North_FIPS_4601	6596	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_2011_StatePlane_Washington _North_FIPS_4601_Ft_US	6597	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_2011_StatePlane_Washington _South_FIPS_4602	6598	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_2011_StatePlane_Washington _South_FIPS_4602_Ft_US	6599	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_2011_StatePlane_West_ Virginia_North_FIPS_4701	6600	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_2011_StatePlane_West_ Virginia_North_FIPS_4701_FtUS	6601	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_2011_StatePlane_West_ Virginia_South_FIPS_4702	6602	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_2011_StatePlane_West_ Virginia_South_FIPS_4702_FtUS	6603	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_2011_StatePlane_Wisconsin_ Central_FIPS_4802	6879	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_2011_StatePlane_Wisconsin_ Central_FIPS_4802_Ft_US	6605	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_2011_StatePlane_Wisconsin_ North_FIPS_4801	6606	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_2011_StatePlane_Wisconsin_ North_FIPS_4801_Ft_US	6607	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_2011_StatePlane_Wisconsin_ South_FIPS_4803	6608	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_2011_StatePlane_Wisconsin_ South_FIPS_4803_Ft_US	6609	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_2011_StatePlane_Wyoming_ East_Central_FIPS_4902	6613	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_2011_StatePlane_Wyoming_ East_FIPS_4901	6611	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_2011_StatePlane_Wyoming_ East_FIPS_4901_Ft_US	6612	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_2011_StatePlane_Wyoming_ E_Central_FIPS_4902_Ft_US	6614	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_2011_StatePlane_Wyoming_ W_Central_FIPS_4903_Ft_US	6618	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_2011_StatePlane_Wyoming_ West_Central_FIPS_4903	6617	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_2011_StatePlane_Wyoming_ West_FIPS_4904	6615	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_2011_StatePlane_Wyoming_ West_FIPS_4904_Ft_US	6616	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_2011_Texas_Centric_ Mapping_System_Albers	6579	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_2011_Texas_Centric_ Mapping_System_Lambert	6580	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_2011_UTM_Zone_10N	6339	USA - 126°W to 120°W	30.54	-126	49.09	-119.99
NAD_1983_2011_UTM_Zone_11N	6340	USA - 120°W to 114°W	30.88	-120	49.01	-114
NAD_1983_2011_UTM_Zone_12N	6341	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1983_2011_UTM_Zone_13N	6342	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1983_2011_UTM_Zone_14N	6343	USA - 102°W to 96°W	25.83	-102	49.01	-96
NAD_1983_2011_UTM_Zone_15N	6344	USA - 96°W to 90°W	25.61	-96.01	49.38	-90
NAD_1983_2011_UTM_Zone_16N	6345	USA - 90°W to 84°W	23.97	-90	48.32	-84
NAD_1983_2011_UTM_Zone_17N	6346	USA - 84°W to 78°W	23.81	-84	46.13	-78
NAD_1983_2011_UTM_Zone_18N	6347	USA - 78°W to 72°W	28.28	-78	45.03	-72
NAD_1983_2011_UTM_Zone_19N	6348	USA - 72°W to 66°W	33.61	-72	47.47	-65.99
NAD_1983_2011_UTM_Zone_1N	6330	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1983_2011_UTM_Zone_20N	102045	Caribbean - Puerto Rico and US Virgin Islands	14.92	-68.49	21.86	-63.88
NAD_1983_2011_UTM_Zone_2N	6331	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1983_2011_UTM_Zone_3N	6332	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_2011_UTM_Zone_4N	6333	USA - 162°W to 156°W - AK, OCS	50.98	-162	74.71	-155.99
NAD_1983_2011_UTM_Zone_59N	6328	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1983_2011_UTM_Zone_5N	6334	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1983_2011_UTM_Zone_60N	6329	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1983_2011_UTM_Zone_6N	6335	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1983_2011_UTM_Zone_7N	6336	USA - 144°W to 138°W	53.47	-144	73.59	-137.99
NAD_1983_2011_UTM_Zone_8N	6337	USA - 138°W to 132°W	53.6	-138	73.04	-131.99
NAD_1983_2011_UTM_Zone_9N	6338	USA - 132°W to 126°W	35.38	-132	56.84	-126
NAD_1983_2011_Virginia_Lambert	6591	USA - Virginia	36.54	-83.68	39.46	-75.31
NAD_1983_2011_Wisconsin_TM	6610	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_2011_Wisconsin_TM_US_Ft	102974	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_2011_WISCRS_Adams_and_ Juneau_Feet	7587	USA - Wisconsin - Adams and Juneau	43.64	-90.32	44.25	-89.59
NAD_1983_2011_WISCRS_Adams_and_ Juneau_Meters	7528	USA - Wisconsin - Adams and Juneau	43.64	-90.32	44.25	-89.59
NAD_1983_2011_WISCRS_Ashland_Feet	7588	USA - Wisconsin - Ashland	45.98	-90.93	47.09	-90.3
NAD_1983_2011_WISCRS_Ashland_ Meters	7529	USA - Wisconsin - Ashland	45.98	-90.93	47.09	-90.3
NAD_1983_2011_WISCRS_Barron_Feet	7589	USA - Wisconsin - Barron	45.2	-92.16	45.65	-91.53
NAD_1983_2011_WISCRS_Barron_ Meters	7530	USA - Wisconsin - Barron	45.2	-92.16	45.65	-91.53
NAD_1983_2011_WISCRS_Bayfield_Feet	7590	USA - Wisconsin - Bayfield	46.15	-91.56	47.01	-90.75
NAD_1983_2011_WISCRS_Bayfield_ Meters	7531	USA - Wisconsin - Bayfield	46.15	-91.56	47.01	-90.75
NAD_1983_2011_WISCRS_Brown_Feet	7591	USA - Wisconsin - Brown	44.24	-88.26	44.68	-87.76
NAD_1983_2011_WISCRS_Brown_Meters	7532	USA - Wisconsin - Brown	44.24	-88.26	44.68	-87.76
NAD_1983_2011_WISCRS_Buffalo_Feet	7592	USA - Wisconsin - Buffalo	44.02	-92.09	44.6	-91.52
NAD_1983_2011_WISCRS_Buffalo_ Meters	7533	USA - Wisconsin - Buffalo	44.02	-92.09	44.6	-91.52
NAD_1983_2011_WISCRS_Burnett_Feet	7593	USA - Wisconsin - Burnett	45.63	-92.89	46.16	-92.03
NAD_1983_2011_WISCRS_Burnett_ Meters	7534	USA - Wisconsin - Burnett	45.63	-92.89	46.16	-92.03
NAD_1983_2011_WISCRS_Calumet_ Fond_du_Lac_Outagamie_Winnebago_ Feet	7594	USA - Wisconsin - Calumet, Fond du Lac, Outagamie and Winnebago	43.54	-88.89	44.6	-88.04
NAD_1983_2011_WISCRS_Calumet_ Fond_du_Lac_Outagamie_Winnebago_ Meters	7535	USA - Wisconsin - Calumet, Fond du Lac, Outagamie and Winnebago	43.54	-88.89	44.6	-88.04
NAD_1983_2011_WISCRS_Chippewa_ Feet	7595	USA - Wisconsin - Chippewa	44.85	-91.67	45.3	-90.92
NAD_1983_2011_WISCRS_Chippewa_ Meters	7536	USA - Wisconsin - Chippewa	44.85	-91.67	45.3	-90.92
NAD_1983_2011_WISCRS_Clark_Feet	7596	USA - Wisconsin - Clark	44.42	-90.93	45.04	-90.31
NAD_1983_2011_WISCRS_Clark_Meters	7537	USA - Wisconsin - Clark	44.42	-90.93	45.04	-90.31
NAD_1983_2011_WISCRS_Columbia_ Feet	7597	USA - Wisconsin - Columbia	43.28	-89.79	43.65	-89
NAD_1983_2011_WISCRS_Columbia_ Meters	7538	USA - Wisconsin - Columbia	43.28	-89.79	43.65	-89
NAD_1983_2011_WISCRS_Crawford_ Feet	7598	USA - Wisconsin - Crawford	42.98	-91.22	43.43	-90.66
NAD_1983_2011_WISCRS_Crawford_ Meters	7539	USA - Wisconsin - Crawford	42.98	-91.22	43.43	-90.66
NAD_1983_2011_WISCRS_Dane_Feet	7599	USA - Wisconsin - Dane	42.84	-89.84	43.3	-89
NAD_1983_2011_WISCRS_Dane_Meters	7540	USA - Wisconsin - Dane	42.84	-89.84	43.3	-89
NAD_1983_2011_WISCRS_Dodge_and_ Jefferson_Feet	7600	USA - Wisconsin - Dodge and Jefferson	42.84	-89.02	43.64	-88.4
NAD_1983_2011_WISCRS_Dodge_and_ Jefferson_Meters	7541	USA - Wisconsin - Dodge and Jefferson	42.84	-89.02	43.64	-88.4
NAD_1983_2011_WISCRS_Door_Feet	7601	USA - Wisconsin - Oneida	45.46	-90.05	45.91	-89.04
NAD_1983_2011_WISCRS_Door_Meters	7542	USA - Wisconsin - Door	44.67	-87.74	45.43	-86.8
NAD_1983_2011_WISCRS_Douglas_Feet	7602	USA - Wisconsin - Douglas	46.15	-92.3	46.76	-91.55
NAD_1983_2011_WISCRS_Douglas_ Meters	7543	USA - Wisconsin - Douglas	46.15	-92.3	46.76	-91.55
NAD_1983_2011_WISCRS_Dunn_Feet	7603	USA - Wisconsin - Dunn	44.68	-92.16	45.21	-91.64
NAD_1983_2011_WISCRS_Dunn_Meters	7544	USA - Wisconsin - Dunn	44.68	-92.16	45.21	-91.64
NAD_1983_2011_WISCRS_Eau_Claire_ Feet	7604	USA - Wisconsin - Eau Claire	44.59	-91.66	44.86	-90.92
NAD_1983_2011_WISCRS_EauClaire_ Meters	7545	USA - Wisconsin - Eau Claire	44.59	-91.66	44.86	-90.92
NAD_1983_2011_WISCRS_Florence_Feet	7605	USA - Wisconsin - Florence	45.71	-88.69	46.03	-88.05
NAD_1983_2011_WISCRS_Florence_ Meters	7546	USA - Wisconsin - Florence	45.71	-88.69	46.03	-88.05
NAD_1983_2011_WISCRS_Forest_Feet	7606	USA - Wisconsin - Forest	45.37	-89.05	46.08	-88.42
NAD_1983_2011_WISCRS_Forest_Meters	7547	USA - Wisconsin - Forest	45.37	-89.05	46.08	-88.42
NAD_1983_2011_WISCRS_Grant_Feet	7607	USA - Wisconsin - Grant	42.5	-91.16	43.22	-90.42
NAD_1983_2011_WISCRS_Grant_Meters	7548	USA - Wisconsin - Grant	42.5	-91.16	43.22	-90.42
NAD_1983_2011_WISCRS_Green_and_ Lafayette_Feet	7608	USA - Wisconsin - Green and Lafayette	42.5	-90.43	42.86	-89.36
NAD_1983_2011_WISCRS_Green_and_ Lafayette_Meters	7549	USA - Wisconsin - Green and Lafayette	42.5	-90.43	42.86	-89.36
NAD_1983_2011_WISCRS_Green_Lake_ and_Marquette_Feet	7609	USA - Wisconsin - Green Lake and Marquette	43.63	-89.6	43.99	-88.88
NAD_1983_2011_WISCRS_Green_Lake_ and_Marquette_Meters	7550	USA - Wisconsin - Green Lake and Marquette	43.63	-89.6	43.99	-88.88
NAD_1983_2011_WISCRS_Iowa_Feet	7610	USA - Wisconsin - Iowa	42.81	-90.43	43.21	-89.83
NAD_1983_2011_WISCRS_Iowa_Meters	7551	USA - Wisconsin - Iowa	42.81	-90.43	43.21	-89.83
NAD_1983_2011_WISCRS_Iron_Feet	7611	USA - Wisconsin - Iron	45.98	-90.56	46.6	-89.92
NAD_1983_2011_WISCRS_Iron_Meters	7552	USA - Wisconsin - Iron	45.98	-90.56	46.6	-89.92
NAD_1983_2011_WISCRS_Jackson_Feet	7612	USA - Wisconsin - Jackson	44.07	-91.17	44.6	-90.31
NAD_1983_2011_WISCRS_Jackson_ Meters	7553	USA - Wisconsin - Jackson	44.07	-91.17	44.6	-90.31
NAD_1983_2011_WISCRS_Kenosha_ Milwaukee_Ozaukee_Racine_Feet	7613	USA - Wisconsin - Kenosha, Milwaukee, Ozaukee and Racine	42.49	-88.31	43.55	-87.75
NAD_1983_2011_WISCRS_Kenosha_ Milwaukee_Ozaukee_Racine_Meters	7554	USA - Wisconsin - Kenosha, Milwaukee, Ozaukee and Racine	42.49	-88.31	43.55	-87.75
NAD_1983_2011_WISCRS_Kewaunee_ Manitowoc_Sheboygan_Feet	7614	USA - Wisconsin - Kewaunee, Manitowoc and Sheboygan	43.54	-88.17	44.68	-87.37
NAD_1983_2011_WISCRS_Kewaunee_ Manitowoc_Sheboygan_Meters	7555	USA - Wisconsin - Kewaunee, Manitowoc and Sheboygan	43.54	-88.17	44.68	-87.37
NAD_1983_2011_WISCRS_La_Crosse_ Feet	7615	USA - Wisconsin - La Crosse	43.72	-91.43	44.1	-90.91
NAD_1983_2011_WISCRS_La_Crosse_ Meters	7556	USA - Wisconsin - La Crosse	43.72	-91.43	44.1	-90.91
NAD_1983_2011_WISCRS_Langlade_Feet	7616	USA - Wisconsin - Langlade	45.02	-89.43	45.48	-88.63
NAD_1983_2011_WISCRS_Langlade_ Meters	7557	USA - Wisconsin - Langlade	45.02	-89.43	45.48	-88.63
NAD_1983_2011_WISCRS_Lincoln_Feet	7617	USA - Wisconsin - Lincoln	45.11	-90.05	45.56	-89.42
NAD_1983_2011_WISCRS_Lincoln_ Meters	7558	USA - Wisconsin - Lincoln	45.11	-90.05	45.56	-89.42
NAD_1983_2011_WISCRS_Marathon_ Feet	7618	USA - Wisconsin - Marathon	44.68	-90.32	45.13	-89.22
NAD_1983_2011_WISCRS_Marathon_ Meters	7559	USA - Wisconsin - Marathon	44.68	-90.32	45.13	-89.22
NAD_1983_2011_WISCRS_Marinette_ Feet	7619	USA - Wisconsin - Marinette	44.96	-88.43	45.8	-87.48
NAD_1983_2011_WISCRS_Marinette_ Meters	7560	USA - Wisconsin - Marinette	44.96	-88.43	45.8	-87.48
NAD_1983_2011_WISCRS_Menominee_ Feet	7620	USA - Wisconsin - Menominee	44.85	-88.99	45.12	-88.48
NAD_1983_2011_WISCRS_Menominee_ Meters	7561	USA - Wisconsin - Menominee	44.85	-88.99	45.12	-88.48
NAD_1983_2011_WISCRS_Monroe_Feet	7621	USA - Wisconsin - Monroe	43.72	-90.98	44.17	-90.31
NAD_1983_2011_WISCRS_Monroe_ Meters	7562	USA - Wisconsin - Monroe	43.72	-90.98	44.17	-90.31
NAD_1983_2011_WISCRS_Oconto_Feet	7622	USA - Wisconsin - Oconto	44.67	-88.69	45.38	-87.76
NAD_1983_2011_WISCRS_Oconto_ Meters	7563	USA - Wisconsin - Oconto	44.67	-88.69	45.38	-87.76
NAD_1983_2011_WISCRS_Oneida_Feet	7623	USA - Wisconsin - Oneida	45.46	-90.05	45.91	-89.04
NAD_1983_2011_WISCRS_Oneida_ Meters	7564	USA - Wisconsin - Oneida	45.46	-90.05	45.91	-89.04
NAD_1983_2011_WISCRS_Pepin_and_ Pierce_Feet	7624	USA - Wisconsin - Pepin and Pierce	44.4	-92.81	44.87	-91.65
NAD_1983_2011_WISCRS_Pepin_and_ Pierce_Meters	7565	USA - Wisconsin - Pepin and Pierce	44.4	-92.81	44.87	-91.65
NAD_1983_2011_WISCRS_Polk_Feet	7625	USA - Wisconsin - Polk	45.2	-92.89	45.73	-92.15
NAD_1983_2011_WISCRS_Polk_Meters	7566	USA - Wisconsin - Polk	45.2	-92.89	45.73	-92.15
NAD_1983_2011_WISCRS_Portage_Feet	7626	USA - Wisconsin - Portage	44.24	-89.85	44.69	-89.22
NAD_1983_2011_WISCRS_Portage_ Meters	7567	USA - Wisconsin - Portage	44.24	-89.85	44.69	-89.22
NAD_1983_2011_WISCRS_Price_Feet	7627	USA - Wisconsin - Price	45.37	-90.68	45.99	-90.04
NAD_1983_2011_WISCRS_Price_Meters	7568	USA - Wisconsin - Price	45.37	-90.68	45.99	-90.04
NAD_1983_2011_WISCRS_Richland_Feet	7628	USA - Wisconsin - Richland	43.16	-90.68	43.56	-90.19
NAD_1983_2011_WISCRS_Richland_ Meters	7569	USA - Wisconsin - Richland	43.16	-90.68	43.56	-90.19
NAD_1983_2011_WISCRS_Rock_Feet	7629	USA - Wisconsin - Rock	42.49	-89.37	42.85	-88.77
NAD_1983_2011_WISCRS_Rock_Meters	7570	USA - Wisconsin - Rock	42.49	-89.37	42.85	-88.77
NAD_1983_2011_WISCRS_Rusk_Feet	7630	USA - Wisconsin - Rusk	45.29	-91.55	45.64	-90.67
NAD_1983_2011_WISCRS_Rusk_Meters	7571	USA - Wisconsin - Rusk	45.29	-91.55	45.64	-90.67
NAD_1983_2011_WISCRS_Sauk_Feet	7631	USA - Wisconsin - Sauk	43.14	-90.32	43.65	-89.59
NAD_1983_2011_WISCRS_Sauk_Meters	7572	USA - Wisconsin - Sauk	43.14	-90.32	43.65	-89.59
NAD_1983_2011_WISCRS_Sawyer_Feet	7632	USA - Wisconsin - Sawyer	45.63	-91.56	46.16	-90.67
NAD_1983_2011_WISCRS_Sawyer_ Meters	7573	USA - Wisconsin - Sawyer	45.63	-91.56	46.16	-90.67
NAD_1983_2011_WISCRS_Shawano_Feet	7633	USA - Wisconsin - Shawano	44.58	-89.23	45.03	-88.24
NAD_1983_2011_WISCRS_Shawano_ Meters	7574	USA - Wisconsin - Shawano	44.58	-89.23	45.03	-88.24
NAD_1983_2011_WISCRS_St_Croix_Feet	7634	USA - Wisconsin - St. Croix	44.85	-92.81	45.22	-92.13
NAD_1983_2011_WISCRS_St_Croix_ Meters	7575	USA - Wisconsin - St. Croix	44.85	-92.81	45.22	-92.13
NAD_1983_2011_WISCRS_Taylor_Feet	7635	USA - Wisconsin - Taylor	45.03	-90.93	45.39	-90.04
NAD_1983_2011_WISCRS_Taylor_Meters	7576	USA - Wisconsin - Taylor	45.03	-90.93	45.39	-90.04
NAD_1983_2011_WISCRS_Trempealeau_ Feet	7636	USA - Wisconsin - Trempealeau	43.98	-91.62	44.6	-91.15
NAD_1983_2011_WISCRS_Trempealeau_ Meters	7577	USA - Wisconsin - Trempealeau	43.98	-91.62	44.6	-91.15
NAD_1983_2011_WISCRS_Vernon_Feet	7637	USA - Wisconsin - Vernon	43.42	-91.28	43.74	-90.31
NAD_1983_2011_WISCRS_Vernon_ Meters	7578	USA - Wisconsin - Vernon	43.42	-91.28	43.74	-90.31
NAD_1983_2011_WISCRS_Vilas_Feet	7638	USA - Wisconsin - Vilas	45.85	-90.05	46.3	-88.93
NAD_1983_2011_WISCRS_Vilas_Meters	7579	USA - Wisconsin - Vilas	45.85	-90.05	46.3	-88.93
NAD_1983_2011_WISCRS_Walworth_ Feet	7639	USA - Wisconsin - Walworth	42.49	-88.78	42.85	-88.3
NAD_1983_2011_WISCRS_Walworth_ Meters	7580	USA - Wisconsin - Walworth	42.49	-88.78	42.85	-88.3
NAD_1983_2011_WISCRS_Washburn_ Feet	7640	USA - Wisconsin - Washburn	45.63	-92.06	46.16	-91.54
NAD_1983_2011_WISCRS_Washburn_ Meters	7581	USA - Wisconsin - Washburn	45.63	-92.06	46.16	-91.54
NAD_1983_2011_WISCRS_Washington_ Feet	7641	USA - Wisconsin - Washington	43.19	-88.42	43.55	-88.03
NAD_1983_2011_WISCRS_Washington_ Meters	7582	USA - Wisconsin - Washington	43.19	-88.42	43.55	-88.03
NAD_1983_2011_WISCRS_Waukesha_ Feet	7642	USA - Wisconsin - Waukesha	42.84	-88.55	43.2	-88.06
NAD_1983_2011_WISCRS_Waukesha_ Meters	7583	USA - Wisconsin - Waukesha	42.84	-88.55	43.2	-88.06
NAD_1983_2011_WISCRS_Waupaca_Feet	7643	USA - Wisconsin - Waupaca	44.24	-89.23	44.69	-88.6
NAD_1983_2011_WISCRS_Waupaca_ Meters	7584	USA - Wisconsin - Waupaca	44.24	-89.23	44.69	-88.6
NAD_1983_2011_WISCRS_Waushara_ Feet	7644	USA - Wisconsin - Waushara	43.98	-89.6	44.25	-88.88
NAD_1983_2011_WISCRS_Waushara_ Meters	7585	USA - Wisconsin - Waushara	43.98	-89.6	44.25	-88.88
NAD_1983_2011_WISCRS_Wood_Feet	7645	USA - Wisconsin - Wood	44.24	-90.32	44.69	-89.72
NAD_1983_2011_WISCRS_Wood_Meters	7586	USA - Wisconsin - Wood	44.24	-90.32	44.69	-89.72
NAD_1983_3TM_111	3775	Canada - Alberta - east of 112.5°W	48.99	-112.5	60	-109.98
NAD_1983_3TM_114	3776	Canada - Alberta - 115.5°W to 112.5°W	48.99	-115.5	60	-112.5
NAD_1983_3TM_117	3777	Canada - Alberta - 118.5°W to 115.5°W	50.77	-118.5	60	-115.5
NAD_1983_3TM_120	3801	Canada - Alberta - west of 118.5°W	52.88	-120	60	-118.5
NAD_1983_Alaska_Albers	3338	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1983_Albers_BLM_MT_ND_SD	102399	USA - Montana, North Dakota, and South Dakota	44.3	-116.1	49.1	-96.3
NAD_1983_BC_Environment_Albers	3005	Canada - British Columbia	48.25	-139.04	60.01	-114.08
NAD_1983_BLM_Zone_10N	4430	USA - 126°W to 120°W	30.54	-126	49.09	-119.99
NAD_1983_BLM_Zone_11N	4431	USA - 120°W to 114°W	30.88	-120	49.01	-114
NAD_1983_BLM_Zone_12N	4432	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1983_BLM_Zone_13N	4433	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1983_BLM_Zone_14N_ftUS	32164	USA - 102°W to 96°W and Gulf of Mexico OCS	25.83	-102	49.01	-95.87
NAD_1983_BLM_Zone_15N_ftUS	32165	USA - 96°W to 90°W and Gulf of Mexico OCS	25.61	-96.01	49.38	-89.86
NAD_1983_BLM_Zone_16N_ftUS	32166	USA - 90°W to 84°W and Gulf of Mexico OCS	23.95	-90.01	48.32	-83.91
NAD_1983_BLM_Zone_17N_ftUS	32167	USA - 84°W to 78°W and Gulf of Mexico OCS	23.81	-84.09	46.13	-77.99
NAD_1983_BLM_Zone_18N	4438	USA - 78°W to 72°W	28.28	-78	45.03	-72
NAD_1983_BLM_Zone_19N	4439	USA - 72°W to 66°W	33.61	-72	47.47	-65.99
NAD_1983_BLM_Zone_1N	4421	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1983_BLM_Zone_2N	4422	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1983_BLM_Zone_3N	4423	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_BLM_Zone_4N	4424	USA - 162°W to 156°W - AK, OCS	50.98	-162	74.71	-155.99
NAD_1983_BLM_Zone_59N	4217	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1983_BLM_Zone_5N	4425	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1983_BLM_Zone_60N	4420	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1983_BLM_Zone_6N	4426	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1983_BLM_Zone_7N	4427	USA - 144°W to 138°W	53.47	-144	73.59	-137.99
NAD_1983_BLM_Zone_8N	4428	USA - 138°W to 132°W	53.6	-138	73.04	-131.99
NAD_1983_BLM_Zone_9N	4429	USA - 132°W to 126°W	35.38	-132	56.84	-126
NAD_1983_California_Teale_Albers	3310	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_California_Teale_Albers_ Ft_Intl	102760	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_California_Teale_Albers_FtUS	102600	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_Canada_Atlas_Lambert	3978	Canada	38.21	-141.01	86.46	-40.73
NAD_1983_Contiguous_USA_Albers	5070	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
NAD_1983_CORS96_Alaska_Albers	102247	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1983_CORS96_Maine_2000_Central _Zone	103373	USA - Maine - CS2000 - Central	43.75	-70.03	47.47	-68.33
NAD_1983_CORS96_Maine_2000_East_ Zone	103372	USA - Maine - CS2000 - East	44.18	-68.58	47.37	-66.91
NAD_1983_CORS96_Maine_2000_West_ Zone	103374	USA - Maine - CS2000 - West	43.07	-71.09	46.58	-69.61
NAD_1983_CORS96_Oregon_Statewide_ Lambert	6867	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_CORS96_Oregon_Statewide_ Lambert_Ft_Intl	6868	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_CORS96_SPCS_Puerto_Rico_ and_Virgin_Islands	6307	Caribbean - Puerto Rico and US Virgin Islands - onshore	17.62	-67.97	18.57	-64.51
NAD_1983_CORS96_StatePlane_Alabama _East_FIPS_0101	103220	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_CORS96_StatePlane_Alabama _West_FIPS_0102	103221	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_CORS96_StatePlane_Alaska_ 10_FIPS_5010	102375	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_CORS96_StatePlane_Alaska_1 _FIPS_5001	102366	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_CORS96_StatePlane_Alaska_2 _FIPS_5002	102367	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_CORS96_StatePlane_Alaska_3 _FIPS_5003	102368	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_CORS96_StatePlane_Alaska_4 _FIPS_5004	102369	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_CORS96_StatePlane_Alaska_5 _FIPS_5005	102370	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_CORS96_StatePlane_Alaska_6 _FIPS_5006	102371	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_CORS96_StatePlane_Alaska_7 _FIPS_5007	102372	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_CORS96_StatePlane_Alaska_8 _FIPS_5008	102373	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_CORS96_StatePlane_Alaska_9 _FIPS_5009	102374	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_CORS96_StatePlane_Arizona_ Central_FIPS_0202	103223	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_CORS96_StatePlane_Arizona_ Central_FIPS_0202_Ft_Intl	103226	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_CORS96_StatePlane_Arizona_ East_FIPS_0201	103222	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_CORS96_StatePlane_Arizona_ East_FIPS_0201_Ft_Intl	103225	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_CORS96_StatePlane_Arizona_ West_FIPS_0203	103224	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_CORS96_StatePlane_Arizona_ West_FIPS_0203_Ft_Intl	103227	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_CORS96_StatePlane_Arkansas _North_FIPS_0301	103228	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_CORS96_StatePlane_Arkansas _North_FIPS_0301_Ft_US	103230	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_CORS96_StatePlane_Arkansas _South_FIPS_0302	103229	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_CORS96_StatePlane_Arkansas _South_FIPS_0302_Ft_US	103231	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_CORS96_StatePlane_ California_I_FIPS_0401	103232	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_CORS96_StatePlane_ California_I_FIPS_0401_Ft_US	103238	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_CORS96_StatePlane_ California_II_FIPS_0402	103233	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_CORS96_StatePlane_ California_II_FIPS_0402_Ft_US	103239	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_CORS96_StatePlane_ California_III_FIPS_0403	103234	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_CORS96_StatePlane_ California_III_FIPS_0403_Ft_US	103240	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_CORS96_StatePlane_ California_IV_FIPS_0404	103235	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_CORS96_StatePlane_ California_IV_FIPS_0404_Ft_US	103241	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_CORS96_StatePlane_ California_V_FIPS_0405	103236	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_CORS96_StatePlane_ California_V_FIPS_0405_Ft_US	103242	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_CORS96_StatePlane_ California_VI_FIPS_0406	103237	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_CORS96_StatePlane_ California_VI_FIPS_0406_Ft_US	103243	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_CORS96_StatePlane_Colorado _Central_FIPS_0502	103245	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_CORS96_StatePlane_Colorado _Central_FIPS_0502_Ft_US	103248	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_CORS96_StatePlane_Colorado _North_FIPS_0501	103244	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_CORS96_StatePlane_Colorado _North_FIPS_0501_Ft_US	103247	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_CORS96_StatePlane_Colorado _South_FIPS_0503	103246	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_CORS96_StatePlane_Colorado _South_FIPS_0503_Ft_US	103249	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_CORS96_StatePlane_ Connecticut_FIPS_0600	103250	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_CORS96_StatePlane_ Connecticut_FIPS_0600_Ft_US	103251	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_CORS96_StatePlane_ Delaware_FIPS_0700	103252	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_CORS96_StatePlane_ Delaware_FIPS_0700_Ft_US	103253	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_CORS96_StatePlane_Florida_ East_FIPS_0901	103254	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_CORS96_StatePlane_Florida_ East_FIPS_0901_Ft_US	103257	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_CORS96_StatePlane_Florida_ North_FIPS_0903	103256	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_CORS96_StatePlane_Florida_ North_FIPS_0903_Ft_US	103259	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_CORS96_StatePlane_Florida_ West_FIPS_0902	103255	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_CORS96_StatePlane_Florida_ West_FIPS_0902_Ft_US	103258	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_CORS96_StatePlane_Georgia_ East_FIPS_1001	103260	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_CORS96_StatePlane_Georgia_ East_FIPS_1001_Ft_US	103262	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_CORS96_StatePlane_Georgia_ West_FIPS_1002	103261	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_CORS96_StatePlane_Georgia_ West_FIPS_1002_Ft_US	103263	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_CORS96_StatePlane_Idaho_ Central_FIPS_1102	103265	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_CORS96_StatePlane_Idaho_ Central_FIPS_1102_Ft_US	103268	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_CORS96_StatePlane_Idaho_ East_FIPS_1101	103264	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_CORS96_StatePlane_Idaho_ East_FIPS_1101_Ft_US	103267	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_CORS96_StatePlane_Idaho_ West_FIPS_1103	103266	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_CORS96_StatePlane_Idaho_ West_FIPS_1103_Ft_US	103269	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_CORS96_StatePlane_Illinois_ East_FIPS_1201	103270	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_CORS96_StatePlane_Illinois_ East_FIPS_1201_Ft_US	103272	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_CORS96_StatePlane_Illinois_ West_FIPS_1202	103271	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_CORS96_StatePlane_Illinois_ West_FIPS_1202_Ft_US	103273	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_CORS96_StatePlane_Indiana_ East_FIPS_1301	103274	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_CORS96_StatePlane_Indiana_ East_FIPS_1301_Ft_US	103276	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_CORS96_StatePlane_Indiana_ West_FIPS_1302	103275	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_CORS96_StatePlane_Indiana_ West_FIPS_1302_Ft_US	103277	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_CORS96_StatePlane_Iowa_ North_FIPS_1401	103278	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_CORS96_StatePlane_Iowa_ North_FIPS_1401_Ft_US	103280	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_CORS96_StatePlane_Iowa_ South_FIPS_1402	103279	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_CORS96_StatePlane_Iowa_ South_FIPS_1402_Ft_US	103281	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_CORS96_StatePlane_Kansas_ North_FIPS_1501	103282	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_CORS96_StatePlane_Kansas_ North_FIPS_1501_Ft_US	103284	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_CORS96_StatePlane_Kansas_ South_FIPS_1502	103283	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_CORS96_StatePlane_Kansas_ South_FIPS_1502_Ft_US	103285	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_CORS96_StatePlane_ Kentucky_FIPS_1600	103288	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_CORS96_StatePlane_ Kentucky_FIPS_1600_Ft_US	103289	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_CORS96_StatePlane_ Kentucky_North_FIPS_1601	103286	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_CORS96_StatePlane_ Kentucky_North_FIPS_1601_Ft_US	103287	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_CORS96_StatePlane_ Kentucky_South_FIPS_1602	103290	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_CORS96_StatePlane_ Kentucky_South_FIPS_1602_Ft_US	103291	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_CORS96_StatePlane_ Louisiana_North_FIPS_1701	103292	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_CORS96_StatePlane_ Louisiana_North_FIPS_1701_Ft_US	103294	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_CORS96_StatePlane_ Louisiana_South_FIPS_1702	103293	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_CORS96_StatePlane_ Louisiana_South_FIPS_1702_Ft_US	103295	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_CORS96_StatePlane_Maine_ East_FIPS_1801	103296	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_CORS96_StatePlane_Maine_ East_FIPS_1801_Ft_US	103298	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_CORS96_StatePlane_Maine_ West_FIPS_1802	103297	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_CORS96_StatePlane_Maine_ West_FIPS_1802_Ft_US	103299	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_CORS96_StatePlane_ Maryland_FIPS_1900	103375	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_CORS96_StatePlane_ Maryland_FIPS_1900_Ft_US	103376	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_CORS96_StatePlane_ Massachusetts_Island_FIPS_2002	103378	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_CORS96_StatePlane_ Massachusetts_Isl_FIPS_2002_FtUS	103380	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_CORS96_StatePlane_ Massachusetts_Mainland_FIPS_2001	103377	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_CORS96_StatePlane_ Massachusetts_Mnld_FIPS_2001_FtUS	103379	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_CORS96_StatePlane_ Michigan_Central_FIPS_2112	103382	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_CORS96_StatePlane_ Michigan_Central_FIPS_2112_Ft_Intl	103385	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_CORS96_StatePlane_ Michigan_North_FIPS_2111	103381	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_CORS96_StatePlane_ Michigan_North_FIPS_2111_Ft_Intl	103384	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_CORS96_StatePlane_ Michigan_South_FIPS_2113	103383	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_CORS96_StatePlane_ Michigan_South_FIPS_2113_Ft_Intl	103386	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_CORS96_StatePlane_ Minnesota_Central_FIPS_2202	103388	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_CORS96_StatePlane_ Minnesota_Central_FIPS_2202_Ft_US	103391	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_CORS96_StatePlane_ Minnesota_North_FIPS_2201	103387	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_CORS96_StatePlane_ Minnesota_North_FIPS_2201_Ft_US	103390	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_CORS96_StatePlane_ Minnesota_South_FIPS_2203	103389	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_CORS96_StatePlane_ Minnesota_South_FIPS_2203_Ft_US	103392	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_CORS96_StatePlane_ Mississippi_East_FIPS_2301	103393	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_CORS96_StatePlane_ Mississippi_East_FIPS_2301_Ft_US	103395	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_CORS96_StatePlane_ Mississippi_West_FIPS_2302	103394	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_CORS96_StatePlane_ Mississippi_West_FIPS_2302_Ft_US	103396	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_CORS96_StatePlane_Missouri _Central_FIPS_2402	103398	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_CORS96_StatePlane_Missouri _East_FIPS_2401	103397	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_CORS96_StatePlane_Missouri _West_FIPS_2403	103399	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_CORS96_StatePlane_ Montana_FIPS_2500	103472	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_CORS96_StatePlane_ Montana_FIPS_2500_Ft_Intl	103473	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_CORS96_StatePlane_ Nebraska_FIPS_2600	103474	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_CORS96_StatePlane_ Nebraska_FIPS_2600_Ft_US	103475	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_CORS96_StatePlane_Nevada_ Central_FIPS_2702	103477	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_CORS96_StatePlane_Nevada_ Central_FIPS_2702_Ft_US	103480	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_CORS96_StatePlane_Nevada_ East_FIPS_2701	103476	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_CORS96_StatePlane_Nevada_ East_FIPS_2701_Ft_US	103479	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_CORS96_StatePlane_Nevada_ West_FIPS_2703	103478	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_CORS96_StatePlane_Nevada_ West_FIPS_2703_Ft_US	103481	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_CORS96_StatePlane_New_ Hampshire_FIPS_2800	103482	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_CORS96_StatePlane_New_ Hampshire_FIPS_2800_Ft_US	103483	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_CORS96_StatePlane_New_ Jersey_FIPS_2900	103484	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_CORS96_StatePlane_New_ Jersey_FIPS_2900_Ft_US	103485	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_CORS96_StatePlane_New_ Mexico_Central_FIPS_3002	103487	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_CORS96_StatePlane_New_ Mexico_Central_FIPS_3002_Ft_US	103490	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_CORS96_StatePlane_New_ Mexico_East_FIPS_3001	103486	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_CORS96_StatePlane_New_ Mexico_East_FIPS_3001_Ft_US	103489	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_CORS96_StatePlane_New_ Mexico_West_FIPS_3003	103488	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_CORS96_StatePlane_New_ Mexico_West_FIPS_3003_Ft_US	103491	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_CORS96_StatePlane_New_ York_Central_FIPS_3102	103493	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_CORS96_StatePlane_New_ York_Central_FIPS_3102_Ft_US	103497	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_CORS96_StatePlane_New_ York_East_FIPS_3101	103492	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_CORS96_StatePlane_New_ York_East_FIPS_3101_Ft_US	103496	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_CORS96_StatePlane_New_ York_Long_Island_FIPS_3104	103495	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_CORS96_StatePlane_New_ York_Long_Isl_FIPS_3104_Ft_US	103499	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_CORS96_StatePlane_New_ York_West_FIPS_3103	103494	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_CORS96_StatePlane_New_ York_West_FIPS_3103_Ft_US	103498	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_CORS96_StatePlane_North_ Carolina_FIPS_3200	103500	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_CORS96_StatePlane_North_ Carolina_FIPS_3200_Ft_US	103501	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_CORS96_StatePlane_North_ Dakota_North_FIPS_3301	103502	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_CORS96_StatePlane_North_ Dakota_North_FIPS_3301_FtI	103504	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_CORS96_StatePlane_North_ Dakota_South_FIPS_3302	103503	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_CORS96_StatePlane_North_ Dakota_South_FIPS_3302_FtI	103505	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_CORS96_StatePlane_Ohio_ North_FIPS_3401	103506	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_CORS96_StatePlane_Ohio_ North_FIPS_3401_Ft_US	103508	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_CORS96_StatePlane_Ohio_ South_FIPS_3402	103507	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_CORS96_StatePlane_Ohio_ South_FIPS_3402_Ft_US	103509	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_CORS96_StatePlane_ Oklahoma_North_FIPS_3501	103510	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_CORS96_StatePlane_ Oklahoma_North_FIPS_3501_Ft_US	103512	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_CORS96_StatePlane_ Oklahoma_South_FIPS_3502	103511	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_CORS96_StatePlane_ Oklahoma_South_FIPS_3502_Ft_US	103513	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_CORS96_StatePlane_Oregon_ North_FIPS_3601	6884	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_CORS96_StatePlane_Oregon_ North_FIPS_3601_Ft_Intl	6885	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_CORS96_StatePlane_Oregon_ South_FIPS_3602	6886	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_CORS96_StatePlane_Oregon_ South_FIPS_3602_Ft_Intl	6887	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_CORS96_StatePlane_ Pennsylvania_North_FIPS_3701	103514	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_CORS96_StatePlane_ Pennsylvania_North_FIPS_3701_Ft_US	103515	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_CORS96_StatePlane_ Pennsylvania_South_FIPS_3702	103516	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_CORS96_StatePlane_ Pennsylvania_South_FIPS_3702_Ft_US	103517	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_CORS96_StatePlane_Rhode_ Island_FIPS_3800	103518	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_CORS96_StatePlane_Rhode_ Island_FIPS_3800_Ft_US	103519	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_CORS96_StatePlane_South_ Carolina_FIPS_3900	103520	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_CORS96_StatePlane_South_ Carolina_FIPS_3900_Ft_Intl	103521	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_CORS96_StatePlane_South_ Dakota_North_FIPS_4001	103522	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_CORS96_StatePlane_South_ Dakota_North_FIPS_4001_Ft_US	103524	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_CORS96_StatePlane_South_ Dakota_South_FIPS_4002	103523	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_CORS96_StatePlane_South_ Dakota_South_FIPS_4002_Ft_US	103525	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_CORS96_StatePlane_ Tennessee_FIPS_4100	103526	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_CORS96_StatePlane_ Tennessee_FIPS_4100_Ft_US	103527	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_CORS96_StatePlane_Texas_ Central_FIPS_4203	103541	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_CORS96_StatePlane_Texas_ Central_FIPS_4203_Ft_US	103546	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_CORS96_StatePlane_Texas_ North_Central_FIPS_4202	103540	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_CORS96_StatePlane_Texas_ North_Central_FIPS_4202_FtUS	103545	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_CORS96_StatePlane_Texas_ North_FIPS_4201	103539	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_CORS96_StatePlane_Texas_ North_FIPS_4201_Ft_US	103544	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_CORS96_StatePlane_Texas_ South_Central_FIPS_4204	103542	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_CORS96_StatePlane_Texas_ South_Central_FIPS_4204_FtUS	103547	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_CORS96_StatePlane_Texas_ South_FIPS_4205	103543	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_CORS96_StatePlane_Texas_ South_FIPS_4205_Ft_US	103548	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_CORS96_StatePlane_Utah_ Central_FIPS_4302	103550	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_CORS96_StatePlane_Utah_ Central_FIPS_4302_Ft_Intl	103553	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_CORS96_StatePlane_Utah_ Central_FIPS_4302_Ft_US	103556	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_CORS96_StatePlane_Utah_ North_FIPS_4301	103549	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_CORS96_StatePlane_Utah_ North_FIPS_4301_Ft_Intl	103552	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_CORS96_StatePlane_Utah_ North_FIPS_4301_Ft_US	103555	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_CORS96_StatePlane_Utah_ South_FIPS_4303	103551	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_CORS96_StatePlane_Utah_ South_FIPS_4303_Ft_Intl	103554	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_CORS96_StatePlane_Utah_ South_FIPS_4303_Ft_US	103557	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_CORS96_StatePlane_Vermont _FIPS_4400	103558	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_CORS96_StatePlane_Virginia_ North_FIPS_4501	103559	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_CORS96_StatePlane_Virginia_ North_FIPS_4501_Ft_US	103561	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_CORS96_StatePlane_Virginia_ South_FIPS_4502	103560	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_CORS96_StatePlane_Virginia_ South_FIPS_4502_Ft_US	103562	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_CORS96_StatePlane_ Washington_North_FIPS_4601	103563	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_CORS96_StatePlane_ Washington_North_FIPS_4601_Ft_US	103565	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_CORS96_StatePlane_ Washington_South_FIPS_4602	103564	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_CORS96_StatePlane_ Washington_South_FIPS_4602_Ft_US	103566	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_CORS96_StatePlane_West_ Virginia_North_FIPS_4701	103567	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_CORS96_StatePlane_West_ Virginia_North_FIPS_4701_FtUS	103569	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_CORS96_StatePlane_West_ Virginia_South_FIPS_4702	103568	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_CORS96_StatePlane_West_ Virginia_South_FIPS_4702_FtUS	103570	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_CORS96_StatePlane_ Wisconsin_Central_FIPS_4802	103572	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_CORS96_StatePlane_ Wisconsin_Central_FIPS_4802_Ft_US	103575	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_CORS96_StatePlane_ Wisconsin_North_FIPS_4801	103571	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_CORS96_StatePlane_ Wisconsin_North_FIPS_4801_Ft_US	103574	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_CORS96_StatePlane_ Wisconsin_South_FIPS_4803	103573	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_CORS96_StatePlane_ Wisconsin_South_FIPS_4803_Ft_US	103576	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_CORS96_StatePlane_ Wyoming_East_Central_FIPS_4902	103578	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_CORS96_StatePlane_ Wyoming_East_FIPS_4901	103577	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_CORS96_StatePlane_ Wyoming_East_FIPS_4901_Ft_US	103581	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_CORS96_StatePlane_ Wyoming_E_Central_FIPS_4902_Ft_US	103582	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_CORS96_StatePlane_ Wyoming_W_Central_FIPS_4903_Ft_US	103583	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_CORS96_StatePlane_ Wyoming_West_Central_FIPS_4903	103579	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_CORS96_StatePlane_ Wyoming_West_FIPS_4904	103580	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_CORS96_StatePlane_ Wyoming_West_FIPS_4904_Ft_US	103585	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_CORS96_UTM_Zone_10N	102410	USA - 126°W to 120°W	30.54	-126	49.09	-119.99
NAD_1983_CORS96_UTM_Zone_11N	102411	USA - 120°W to 114°W	30.88	-120	49.01	-114
NAD_1983_CORS96_UTM_Zone_12N	102412	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1983_CORS96_UTM_Zone_13N	102413	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1983_CORS96_UTM_Zone_14N	102414	USA - 102°W to 96°W	25.83	-102	49.01	-96
NAD_1983_CORS96_UTM_Zone_15N	102415	USA - 96°W to 90°W	25.61	-96.01	49.38	-90
NAD_1983_CORS96_UTM_Zone_16N	102416	USA - 90°W to 84°W	23.97	-90	48.32	-84
NAD_1983_CORS96_UTM_Zone_17N	102417	USA - 84°W to 78°W	23.81	-84	46.13	-78
NAD_1983_CORS96_UTM_Zone_18N	102418	USA - 78°W to 72°W	28.28	-78	45.03	-72
NAD_1983_CORS96_UTM_Zone_19N	102419	USA - 72°W to 66°W	33.61	-72	47.47	-65.99
NAD_1983_CORS96_UTM_Zone_1N	102401	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1983_CORS96_UTM_Zone_20N	102043	Caribbean - Puerto Rico and US Virgin Islands	14.92	-68.49	21.86	-63.88
NAD_1983_CORS96_UTM_Zone_2N	102402	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1983_CORS96_UTM_Zone_3N	102403	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_CORS96_UTM_Zone_4N	102404	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_CORS96_UTM_Zone_59N	102364	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1983_CORS96_UTM_Zone_5N	102405	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1983_CORS96_UTM_Zone_60N	102365	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1983_CORS96_UTM_Zone_6N	102406	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1983_CORS96_UTM_Zone_7N	102407	USA - 144°W to 138°W	53.47	-144	73.59	-137.99
NAD_1983_CORS96_UTM_Zone_8N	102408	USA - 138°W to 132°W	53.6	-138	73.04	-131.99
NAD_1983_CORS96_UTM_Zone_9N	102409	USA - 132°W to 126°W	35.38	-132	56.84	-126
NAD_1983_CSRS_10TM_AEP_Forest	3402	Canada - Alberta	48.99	-120	60	-109.98
NAD_1983_CSRS_10TM_AEP_Resource	3403	Canada - Alberta	48.99	-120	60	-109.98
NAD_1983_CSRS_3TM_111	3779	Canada - Alberta - east of 112.5°W	48.99	-112.5	60	-109.98
NAD_1983_CSRS_3TM_114	3780	Canada - Alberta - 115.5°W to 112.5°W	48.99	-115.5	60	-112.5
NAD_1983_CSRS_3TM_117	3781	Canada - Alberta - 118.5°W to 115.5°W	50.77	-118.5	60	-115.5
NAD_1983_CSRS_3TM_120	3802	Canada - Alberta - west of 118.5°W	52.88	-120	60	-118.5
NAD_1983_CSRS_BC_Environment_ Albers	3153	Canada - British Columbia	48.25	-139.04	60.01	-114.08
NAD_1983_CSRS_Canada_Atlas_Lambert	3979	Canada	38.21	-141.01	86.46	-40.73
NAD_1983_CSRS_EPSG_Arctic_zone_1-23	6098	Arctic - 87°50'N to 82°50'N, 120°W to 60°W	82.83	-120	87.84	-60
NAD_1983_CSRS_EPSG_Arctic_zone_2-14	6099	Arctic - 84°30'N to 79°30'N, 135°W to 95°W	79.5	-135	84.51	-95
NAD_1983_CSRS_EPSG_Arctic_zone_2-16	6100	Arctic - 84°30'N to 79°30'N, 95°W to 55°W	79.5	-95	84.51	-55
NAD_1983_CSRS_EPSG_Arctic_zone_3-25	6101	Arctic - 81°10'N to 76°10'N, 144°W to 114°W	76.16	-144	81.17	-114
NAD_1983_CSRS_EPSG_Arctic_zone_3-27	6102	Arctic - 81°10'N to 76°10'N, 114°W to 84°W	76.16	-114	81.17	-84
NAD_1983_CSRS_EPSG_Arctic_zone_3-29	6103	Arctic - 81°10'N to 76°10'N, Canada east of 84°W	76.16	-84	81.17	-64.78
NAD_1983_CSRS_EPSG_Arctic_zone_4-14	6104	Arctic - 77°50'N to 72°50'N, 141°W to 116°W	72.83	-141	77.84	-116
NAD_1983_CSRS_EPSG_Arctic_zone_4-16	6105	Arctic - 77°50'N to 72°50'N, 116°W to 91°W	72.83	-116	77.84	-91
NAD_1983_CSRS_EPSG_Arctic_zone_4-18	6106	Arctic - 77°50'N to 72°50'N, 91°W to 67°W	72.83	-91	77.84	-67
NAD_1983_CSRS_EPSG_Arctic_zone_5-33	6107	Arctic - 74°30'N to 69°30'N, 141°W to 121°W	69.5	-141	74.51	-121
NAD_1983_CSRS_EPSG_Arctic_zone_5-35	6108	Arctic - 74°30'N to 69°30'N, 121°W to 101°W	69.5	-121	74.51	-101
NAD_1983_CSRS_EPSG_Arctic_zone_5-37	6109	Arctic - 74°30'N to 69°30'N, 101°W to 81°W	69.5	-101	74.51	-81
NAD_1983_CSRS_EPSG_Arctic_zone_5-39	6110	Arctic - 74°30'N to 69°30'N, 81°W to 61°W	69.5	-81	74.51	-61
NAD_1983_CSRS_EPSG_Arctic_zone_6-18	6111	Arctic - 71°10'N to 66°10'N, 141°W to 122°W	66.16	-141	71.17	-122
NAD_1983_CSRS_EPSG_Arctic_zone_6-20	6112	Arctic - 71°10'N to 66°10'N, 122°W to 103°W	66.16	-122	71.17	-103
NAD_1983_CSRS_EPSG_Arctic_zone_6-22	6113	Arctic - 71°10'N to 66°10'N, 103°W to 84°W	66.16	-103	71.17	-84
NAD_1983_CSRS_EPSG_Arctic_zone_6-24	6114	Arctic - 71°10'N to 66°10'N, 84°W to 65°W	66.16	-84	71.17	-65
NAD_1983_CSRS_MTM_1	26898	Canada - Newfoundland - east of 54.5°W	46.56	-54.5	49.89	-52.54
NAD_1983_CSRS_MTM_10	2952	Canada - Quebec and Ontario - MTM zone 10	42.26	-81	62.45	-78
NAD_1983_CSRS_MTM_11	26891	Canada - Ontario - MTM zone 11	41.67	-83.6	46	-81
NAD_1983_CSRS_MTM_12	26892	Canada - Ontario - MTM zone 12	46	-82.5	55.21	-79.5
NAD_1983_CSRS_MTM_13	26893	Canada - Ontario - MTM zone 13	46	-85.5	55.59	-82.5
NAD_1983_CSRS_MTM_14	26894	Canada - Ontario - 88.5°W to 85.5°W	47.17	-88.5	56.7	-85.5
NAD_1983_CSRS_MTM_15	26895	Canada - Ontario - 91.5°W to 88.5°W	47.97	-91.5	56.9	-88.5
NAD_1983_CSRS_MTM_16	26896	Canada - Ontario - 94.5°W to 91.5°W	48.06	-94.5	55.2	-91.5
NAD_1983_CSRS_MTM_17	26897	Canada - Ontario - west of 94.5°W	48.69	-95.16	53.24	-94.5
NAD_1983_CSRS_MTM_2	26899	Canada - Newfoundland and Labrador - 57.5°W to 54.5°W	46.81	-57.5	54.71	-54.5
NAD_1983_CSRS_MTM_2_SCoPQ	2944	Canada - Quebec - east of 57°W	46.6	-57	53.76	-54
NAD_1983_CSRS_MTM_3	2945	Canada - Quebec, Newfoundland and Labrador - MTM zone 3	47.5	-60	55.38	-57.1
NAD_1983_CSRS_MTM_4	2946	Canada - Quebec and Labrador - 63°W to 60°W	47.16	-63	58.92	-60
NAD_1983_CSRS_MTM_5	2947	Canada - Quebec and Labrador - 66°W to 63°W	47.95	-66	60.52	-63
NAD_1983_CSRS_MTM_6	2948	Canada - Quebec and Labrador - 69°W to 66°W	47.31	-69	59	-66
NAD_1983_CSRS_MTM_7	2949	Canada - Quebec - 72°W to 69°W	45.01	-72	61.8	-69
NAD_1983_CSRS_MTM_8	2950	Canada - Quebec and Ontario - 75°W to 72°W	44.98	-75	62.53	-72
NAD_1983_CSRS_MTM_9	2951	Canada - Quebec and Ontario - 78°W to 75°W	43.63	-78	62.65	-75
NAD_1983_(CSRS)_MTM_Nova_Scotia_4	8082	Canada - Nova Scotia - east of 63°W	44.64	-63	47.08	-59.73
NAD_1983_(CSRS)_MTM_ Nova_Scotia_5	8083	Canada - Nova Scotia - west of 63°W	43.41	-66.28	46.02	-63
NAD_1983_CSRS_MTQ_Lambert	3799	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_CSRS_New_Brunswick_Stereo graphic	2953	Canada - New Brunswick	44.56	-69.05	48.07	-63.7
NAD_1983_CSRS_Northwest_Territories_ Lambert	3581	Canada - NWT	59.98	-136.46	78.81	-102
NAD_1983_CSRS_Ontario_MNR_Lambert	3162	Canada - Ontario	41.67	-95.16	56.9	-74.35
NAD_1983_CSRS_Prince_Edward_Island	2954	Canada - Prince Edward Island	45.9	-64.49	47.09	-61.9
NAD_1983_CSRS_Quebec_Albers	6624	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_CSRS_Quebec_Lambert	6622	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_CSRS_Statistics_Canada_ Lambert	3348	Canada	38.21	-141.01	86.46	-40.73
NAD_1983_CSRS_Teranet_Ontario_ Lambert	5321	Canada - Ontario	41.67	-95.16	56.9	-74.35
NAD_1983_CSRS_UTM_Zone_10N	3157	Canada - 126°W to 120°W	48.13	-126	81.8	-120
NAD_1983_CSRS_UTM_Zone_11N	2955	Canada - 120°W to 114°W	48.99	-120	83.5	-114
NAD_1983_CSRS_UTM_Zone_12N	2956	Canada - 114°W to 108°W	48.99	-114	84	-108
NAD_1983_CSRS_UTM_Zone_13N	2957	Canada - 108°W to 102°W	48.99	-108	84	-102
NAD_1983_CSRS_UTM_Zone_14N	3158	Canada - 102°W to 96°W	48.99	-102	84	-96
NAD_1983_CSRS_UTM_Zone_15N	3159	Canada - 96°W to 90°W	48.03	-96	84	-90
NAD_1983_CSRS_UTM_Zone_16N	3160	Canada - 90°W to 84°W	46.11	-90	84	-84
NAD_1983_CSRS_UTM_Zone_17N	2958	Canada - 84°W to 78°W	41.67	-84	84	-78
NAD_1983_CSRS_UTM_Zone_18N	2959	Canada - 78°W to 72°W	43.63	-78	84	-72
NAD_1983_CSRS_UTM_Zone_19N	2960	Canada - 72°W to 66°W	40.8	-72	84	-66
NAD_1983_CSRS_UTM_Zone_20N	2961	Canada - 66°W to 60°W	40.04	-66	84	-60
NAD_1983_CSRS_UTM_Zone_21N	2962	Canada - 60°W to 54°W	38.56	-60	84	-54
NAD_1983_CSRS_UTM_Zone_22N	3761	Canada - 54°W to 48°W	39.5	-54	57.65	-48
NAD_1983_CSRS_UTM_Zone_23N	9709	Canada - 48°W to 42°W	39.85	-48	54.47	-42
NAD_1983_CSRS_UTM_Zone_24N	9713	Canada - east of 42°W	45.53	-42	49.53	-40.73
NAD_1983_CSRS_UTM_Zone_7N	3154	Canada - 144°W to 138°W	52.05	-141.01	72.53	-138
NAD_1983_CSRS_UTM_Zone_8N	3155	Canada - 138°W to 132°W	48.06	-138	79.42	-132
NAD_1983_CSRS_UTM_Zone_9N	3156	Canada - 132°W to 126°W	46.52	-132	80.93	-126
NAD_1983_(CSRS)_v6_UTM_Zone_15N	103873	Canada - 96~W to 90~W	48.03	-96	84	-90
NAD_1983_(CSRS)_v6_UTM_Zone_16N	103874	Canada - 90~W to 84~W	46.11	-90	84	-84
NAD_1983_(CSRS)_v6_UTM_Zone_17N	103875	Canada - 84~W to 78~W	41.67	-84	84	-78
NAD_1983_(CSRS)_v6_UTM_Zone_18N	103876	Canada - 78~W to 72~W	43.63	-78	84	-72
NAD_1983_(CSRS)_v6_UTM_Zone_19N	103696	Canada - 72°W to 66°W	40.8	-72	84	-66
NAD_1983_(CSRS)_v6_UTM_Zone_20N	103697	Canada - 66°W to 60°W	40.04	-66	84	-60
NAD_1983_(CSRS)_v6_UTM_Zone_21N	103698	Canada - 60°W to 54°W	38.56	-60	84	-54
NAD_1983_CSRS_Yukon_Albers	3579	Canada - Yukon	59.99	-141.01	69.7	-123.91
NAD_1983_Fargo_Ground_Coordinate_ System	102389	USA - North Dakota - Fargo	46.7	-96.93	47	-96.75
NAD_1983_Florida_GDL_Albers	3086	USA - Florida	24.41	-87.63	31.01	-79.97
NAD_1983_Georgia_Statewide_Lambert	102604	USA - Georgia	30.36	-85.61	35.01	-80.77
NAD_1983_Great_Lakes_and_St_ Lawrence_Albers	3175	North America - Great Lakes basin and St Lawrence Seaway	40.99	-93.17	52.22	-54.75
NAD_1983_Great_Lakes_Basin_Albers	3174	North America - Great Lakes basin	40.99	-93.17	50.74	-74.47
NAD_1983_HARN_Adj_MN_Aitkin_Feet	103700	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Aitkin_Meter s	103600	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Anoka_Feet	103708	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Anoka_ Meters	103608	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Becker_Feet	103709	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Becker_ Meters	103609	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Beltrami_ North_Feet	103710	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Beltrami_ North_Meters	103610	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Beltrami_ South_Feet	103711	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Beltrami_ South_Meters	103611	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Benton_Feet	103712	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Benton_ Meters	103612	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Big_Stone_ Feet	103713	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Big_Stone_ Meters	103613	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Blue_Earth_ Feet	103714	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Blue_Earth_ Meters	103614	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Brown_Feet	103715	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Brown_ Meters	103615	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Carlton_Feet	103716	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Carlton_ Meters	103616	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Carver_Feet	103717	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Carver_ Meters	103617	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cass_North_ Feet	103718	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cass_North_ Meters	103618	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cass_South_ Feet	103719	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cass_South_ Meters	103619	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Chippewa_ Feet	103720	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Chippewa_ Meters	103620	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Chisago_Feet	103721	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Chisago_ Meters	103621	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Clay_Feet	103701	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Clay_Meters	103601	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Clearwater_ Feet	103702	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Clearwater_ Meters	103602	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cook_North_ Feet	103722	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cook_North_ Meters	103622	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cook_South_ Feet	103723	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cook_South_ Meters	103623	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cottonwood _Feet	103724	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Cottonwood _Meters	103624	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Crow_Wing_ Feet	103725	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Crow_Wing_ Meters	103625	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Dakota_Feet	103726	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Dakota_ Meters	103626	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Dodge_Feet	103727	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Dodge_ Meters	103627	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Douglas_Feet	103728	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Douglas_ Meters	103628	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Faribault_ Feet	103729	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Faribault_ Meters	103629	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Fillmore_ Feet	103730	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Fillmore_ Meters	103630	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Freeborn_ Feet	103731	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Freeborn_ Meters	103631	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Goodhue_ Feet	103732	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Goodhue_ Meters	103632	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Grant_Feet	103733	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Grant_ Meters	103633	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Hennepin_ Feet	103734	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Hennepin_ Meters	103634	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Houston_ Feet	103735	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Houston_ Meters	103635	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Hubbard_ Feet	103703	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Hubbard_ Meters	103603	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Isanti_Feet	103736	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Isanti_ Meters	103636	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Itasca_North _Feet	103737	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Itasca_North _Meters	103637	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Itasca_South _Feet	103738	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Itasca_South _Meters	103638	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Jackson_Feet	103739	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Jackson_ Meters	103639	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kanabec_ Feet	103740	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kanabec_ Meters	103640	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kandiyohi_ Feet	103741	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kandiyohi_ Meters	103641	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kittson_Feet	103742	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Kittson_ Meters	103642	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Koochiching_ Feet	103743	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Koochiching_ Meters	103643	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lac_Qui_ Parle_Feet	103744	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lac_Qui_ Parle_Meters	103644	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_Feet	103704	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_Meters	103604	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_of_the_ Woods_North_Feet	103745	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_of_the_ Woods_North_Meters	103645	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_of_the_ Woods_South_Feet	103746	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lake_of_the_ Woods_South_Meters	103646	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Le_Sueur_ Feet	103747	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Le_Sueur_ Meters	103647	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lincoln_Feet	103748	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lincoln_ Meters	103648	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lyon_Feet	103749	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Lyon_Meters	103649	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mahnomen_ Feet	103751	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mahnomen_ Meters	103651	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Marshall_ Feet	103752	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Marshall_ Meters	103652	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Martin_Feet	103753	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Martin_ Meters	103653	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_McLeod_Feet	103750	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_McLeod_ Meters	103650	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Meeker_Feet	103754	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Meeker_ Meters	103654	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mille_Lacs_ Feet	103705	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mille_Lacs_ Meters	103605	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Morrison_ Feet	103755	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Morrison_ Meters	103655	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mower_Feet	103756	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Mower_ Meters	103656	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Murray_Feet	103757	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Murray_ Meters	103657	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Nicollet_Feet	103758	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Nicollet_ Meters	103658	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Nobles_Feet	103759	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Nobles_ Meters	103659	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Norman_ Feet	103760	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Norman_ Meters	103660	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Olmsted_ Feet	103761	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Olmsted_ Meters	103661	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Ottertail_ Feet	103762	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Ottertail_ Meters	103662	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pennington_ Feet	103763	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pennington_ Meters	103663	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pine_Feet	103764	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pine_Meters	103664	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pipestone_ Feet	103765	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pipestone_ Meters	103665	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Polk_Feet	103766	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Polk_Meters	103666	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pope_Feet	103767	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Pope_Meters	103667	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Ramsey_Feet	103768	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Ramsey_ Meters	103668	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Red_Lake_ Feet	103769	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Red_Lake_ Meters	103669	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Redwood_ Feet	103770	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Redwood_ Meters	103670	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Renville_Feet	103771	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Renville_ Meters	103671	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Rice_Feet	103772	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Rice_Meters	103672	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Rock_Feet	103773	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Rock_Meters	103673	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Roseau_Feet	103774	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Roseau_ Meters	103674	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Scott_Feet	103778	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Scott_Meters	103678	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Sherburne_ Feet	103779	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Sherburne_ Meters	103679	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Sibley_Feet	103780	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Sibley_ Meters	103680	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Stearns_Feet	103781	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Stearns_ Meters	103681	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Steele_Feet	103782	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Steele_ Meters	103682	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Stevens_Feet	103783	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Stevens_ Meters	103683	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ Central_Feet	103776	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ Central_Meters	103676	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ CS96_Feet	103695	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ CS96_Meters	103694	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ North_Feet	103775	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ North_Meters	103675	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ South_Feet	103777	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_St_Louis_ South_Meters	103677	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Swift_Feet	103784	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Swift_Meters	103684	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Todd_Feet	103785	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Todd_Meters	103685	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Traverse_ Feet	103786	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Traverse_ Meters	103686	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wabasha_ Feet	103787	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wabasha_ Meters	103687	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wadena_ Feet	103788	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wadena_ Meters	103688	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Waseca_ Feet	103789	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Waseca_ Meters	103689	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Washington_ Feet	103706	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Washington_ Meters	103606	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Watonwan_ Feet	103790	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Watonwan_ Meters	103690	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wilkin_Feet	103707	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wilkin_ Meters	103607	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Winona_Feet	103791	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Winona_ Meters	103691	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wright_Feet	103792	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Wright_ Meters	103692	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Yellow_ Medicine_Feet	103793	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_MN_Yellow_ Medicine_Meters	103693	USA - Minnesota	43.49	-97.22	49.38	-89.49
NAD_1983_HARN_Adj_WI_Chippewa_ Feet	103946	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_Adj_WI_Chippewa_ Meters	103846	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_California_Teale_ Albers	3311	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_HARN_Contiguous_USA_ Albers	5071	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
NAD_1983_HARN_Fargo_Ground_ Coordinate_System	102390	USA - North Dakota - Fargo	46.7	-96.93	47	-96.75
NAD_1983_HARN_Florida_GDL_Albers	3087	USA - Florida	24.41	-87.63	31.01	-79.97
NAD_1983_HARN_Guam_Map_Grid	4414	Guam - onshore	13.18	144.58	13.7	145.01
NAD_1983_HARN_Maine_2000_Central_ Zone	3464	USA - Maine - CS2000 - C	43.75	-70.03	47.47	-68.33
NAD_1983_HARN_Maine_2000_East_ Zone	3075	USA - Maine - CS2000 - E	44.18	-68.58	47.37	-66.91
NAD_1983_HARN_Maine_2000_West_ Zone	3077	USA - Maine - CS2000 - W	43.07	-71.09	46.58	-69.61
NAD_1983_HARN_Michigan_GeoRef_ Meters	3079	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1983_HARN_Mississippi_TM	3815	USA - Mississippi	30.01	-91.65	35.01	-88.09
NAD_1983_HARN_Navajo_Nation_ Coordinate_System_Meters	103586	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_HARN_Navajo_Nation_ Coordinate_System_US_Feet	103587	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_HARN_Navajo_Nation_ Coordinate_System_Intl_Feet	103588	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_HARN_Oregon_Statewide_ Lambert	2993	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_HARN_Oregon_Statewide_ Lambert_Feet_Intl	2994	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_HARN_StatePlane_Alabama_ East_FIPS_0101	2759	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_HARN_StatePlane_Alabama_ West_FIPS_0102	2760	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_HARN_StatePlane_Arizona_ Central_FIPS_0202	2762	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_HARN_StatePlane_Arizona_ Central_FIPS_0202_Feet_Intl	2868	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_HARN_StatePlane_Arizona_ East_FIPS_0201	2761	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_HARN_StatePlane_Arizona_ East_FIPS_0201_Feet_Intl	2867	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_HARN_StatePlane_Arizona_ West_FIPS_0203	2763	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_HARN_StatePlane_Arizona_ West_FIPS_0203_Feet_Intl	2869	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_HARN_StatePlane_Arkansas_ North_FIPS_0301	2764	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_HARN_StatePlane_Arkansas_ North_FIPS_0301_Feet	3441	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_HARN_StatePlane_Arkansas_ South_FIPS_0302	2765	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_HARN_StatePlane_Arkansas_ South_FIPS_0302_Feet	3442	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_HARN_StatePlane_California_ I_FIPS_0401	2766	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_HARN_StatePlane_California_ I_FIPS_0401_Feet	2870	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_HARN_StatePlane_California_ II_FIPS_0402	2767	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_HARN_StatePlane_California_ II_FIPS_0402_Feet	2871	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_HARN_StatePlane_California_ III_FIPS_0403	2768	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_HARN_StatePlane_California_ III_FIPS_0403_Feet	2872	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_HARN_StatePlane_California_ IV_FIPS_0404	2769	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_HARN_StatePlane_California_ IV_FIPS_0404_Feet	2873	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_HARN_StatePlane_California_ V_FIPS_0405	2770	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_HARN_StatePlane_California_ V_FIPS_0405_Feet	2874	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_HARN_StatePlane_California_ VI_FIPS_0406	2771	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_HARN_StatePlane_California_ VI_FIPS_0406_Feet	2875	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_HARN_StatePlane_Colorado_ Central_FIPS_0502	2773	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_HARN_StatePlane_Colorado_ Central_FIPS_0502_Feet	2877	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_HARN_StatePlane_Colorado_ North_FIPS_0501	2772	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_HARN_StatePlane_Colorado_ North_FIPS_0501_Feet	2876	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_HARN_StatePlane_Colorado_ South_FIPS_0503	2774	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_HARN_StatePlane_Colorado_ South_FIPS_0503_Feet	2878	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_HARN_StatePlane_Connectic ut_FIPS_0600	2775	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_HARN_StatePlane_ Connecticut_FIPS_0600_Feet	2879	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_HARN_StatePlane_Delaware_ FIPS_0700	2776	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_HARN_StatePlane_Delaware_ FIPS_0700_Feet	2880	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_HARN_StatePlane_Florida_ East_FIPS_0901	2777	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_HARN_StatePlane_Florida_ East_FIPS_0901_Feet	2881	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_HARN_StatePlane_Florida_ North_FIPS_0903	2779	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_HARN_StatePlane_Florida_ North_FIPS_0903_Feet	2883	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_HARN_StatePlane_Florida_ West_FIPS_0902	2778	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_HARN_StatePlane_Florida_ West_FIPS_0902_Feet	2882	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_HARN_StatePlane_Georgia_ East_FIPS_1001	2780	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_HARN_StatePlane_Georgia_ East_FIPS_1001_Feet	2884	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_HARN_StatePlane_Georgia_ West_FIPS_1002	2781	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_HARN_StatePlane_Georgia_ West_FIPS_1002_Feet	2885	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_HARN_StatePlane_Hawaii_1_ FIPS_5101	2782	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_HARN_StatePlane_Hawaii_1_ FIPS_5101_Feet	102461	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_HARN_StatePlane_Hawaii_2_ FIPS_5102	2783	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_HARN_StatePlane_Hawaii_2_ FIPS_5102_Feet	102462	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_HARN_StatePlane_Hawaii_3_ FIPS_5103	2784	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_HARN_StatePlane_Hawaii_3_ FIPS_5103_Feet	3760	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_HARN_StatePlane_Hawaii_4_ FIPS_5104	2785	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_HARN_StatePlane_Hawaii_4_ FIPS_5104_Feet	102464	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_HARN_StatePlane_Hawaii_5_ FIPS_5105	2786	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_HARN_StatePlane_Hawaii_5_ FIPS_5105_Feet	102465	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_HARN_StatePlane_Idaho_ Central_FIPS_1102	2788	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_HARN_StatePlane_Idaho_ Central_FIPS_1102_Feet	2887	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_HARN_StatePlane_Idaho_East _FIPS_1101	2787	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_HARN_StatePlane_Idaho_East _FIPS_1101_Feet	2886	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_HARN_StatePlane_Idaho_ West_FIPS_1103	2789	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_HARN_StatePlane_Idaho_ West_FIPS_1103_Feet	2888	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_HARN_StatePlane_Illinois_ East_FIPS_1201	2790	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_HARN_StatePlane_Illinois_ East_FIPS_1201_Feet	3443	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_HARN_StatePlane_Illinois_ West_FIPS_1202	2791	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_HARN_StatePlane_Illinois_ West_FIPS_1202_Feet	3444	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_HARN_StatePlane_Indiana_ East_FIPS_1301	2792	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_HARN_StatePlane_Indiana_ East_FIPS_1301_Feet	2967	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_HARN_StatePlane_Indiana_ West_FIPS_1302	2793	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_HARN_StatePlane_Indiana_ West_FIPS_1302_Feet	2968	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_HARN_StatePlane_Iowa_ North_FIPS_1401	2794	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_HARN_StatePlane_Iowa_ North_FIPS_1401_Feet	3425	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_HARN_StatePlane_Iowa_ South_FIPS_1402	2795	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_HARN_StatePlane_Iowa_ South_FIPS_1402_Feet	3426	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_HARN_StatePlane_Kansas_ North_FIPS_1501	2796	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_HARN_StatePlane_Kansas_ North_FIPS_1501_Feet	3427	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_HARN_StatePlane_Kansas_ South_FIPS_1502	2797	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_HARN_StatePlane_Kansas_ South_FIPS_1502_Feet	3428	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_HARN_StatePlane_Kentucky_ FIPS_1600	3090	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_HARN_StatePlane_Kentucky_ FIPS_1600_Feet	3091	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_HARN_StatePlane_Kentucky_ North_FIPS_1601	2798	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_HARN_StatePlane_Kentucky_ North_FIPS_1601_Feet	2891	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_HARN_StatePlane_Kentucky_ South_FIPS_1602	2799	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_HARN_StatePlane_Kentucky_ South_FIPS_1602_Feet	2892	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_HARN_StatePlane_Louisiana_ North_FIPS_1701	2800	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_HARN_StatePlane_Louisiana_ North_FIPS_1701_Feet	3456	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_HARN_StatePlane_Louisiana_ South_FIPS_1702	2801	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_HARN_StatePlane_Louisiana_ South_FIPS_1702_Feet	3457	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_HARN_StatePlane_Maine_ East_FIPS_1801	2802	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_HARN_StatePlane_Maine_ East_FIPS_1801_Feet	26855	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_HARN_StatePlane_Maine_ West_FIPS_1802	2803	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_HARN_StatePlane_Maine_ West_FIPS_1802_Feet	26856	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_HARN_StatePlane_Maryland_ FIPS_1900	2804	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_HARN_StatePlane_Maryland_ FIPS_1900_Feet	2893	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_HARN_StatePlane_ Massachusetts_Island_FIPS_2002	2806	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_HARN_StatePlane_ Massachusetts_Island_FIPS_2002_Feet	2895	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_HARN_StatePlane_ Massachusetts_Mainland_FIPS_2001	2805	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_HARN_StatePlane_Mass- achusetts_Mainland_FIPS_2001_Feet	2894	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_HARN_StatePlane_Michigan_ Central_FIPS_2112	2808	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_HARN_StatePlane_Michigan_ Central_FIPS_2112_Feet_Intl	2897	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_HARN_StatePlane_Michigan_ North_FIPS_2111	2807	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_HARN_StatePlane_Michigan_ North_FIPS_2111_Feet_Intl	2896	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_HARN_StatePlane_Michigan_ South_FIPS_2113	2809	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_HARN_StatePlane_Michigan_ South_FIPS_2113_Feet_Intl	2898	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_HARN_StatePlane_Minnesota _Central_FIPS_2202	2811	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_HARN_StatePlane_Minnesota _Central_FIPS_2202_Feet	26858	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_HARN_StatePlane_Minnesota _North_FIPS_2201	2810	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_HARN_StatePlane_Minnesota _North_FIPS_2201_Feet	26857	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_HARN_StatePlane_Minnesota _South_FIPS_2203	2812	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_HARN_StatePlane_Minnesota _South_FIPS_2203_Feet	26859	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_HARN_StatePlane_Mississippi _East_FIPS_2301	2813	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_HARN_StatePlane_Mississippi _East_FIPS_2301_Feet	2899	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_HARN_StatePlane_Mississippi _West_FIPS_2302	2814	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_HARN_StatePlane_Mississippi _West_FIPS_2302_Feet	2900	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_HARN_StatePlane_Missouri_ Central_FIPS_2402	2816	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_HARN_StatePlane_Missouri_ East_FIPS_2401	2815	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_HARN_StatePlane_Missouri_ West_FIPS_2403	2817	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_HARN_StatePlane_Montana_ FIPS_2500	2818	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_HARN_StatePlane_Montana_ FIPS_2500_Feet_Intl	2901	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_HARN_StatePlane_Nebraska_ FIPS_2600	2819	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_HARN_StatePlane_Nebraska_ FIPS_2600_Feet	26860	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_HARN_StatePlane_Nevada_ Central_FIPS_2702	2821	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_HARN_StatePlane_Nevada_ Central_FIPS_2702_Feet	3430	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_HARN_StatePlane_Nevada_ East_FIPS_2701	2820	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_HARN_StatePlane_Nevada_ East_FIPS_2701_Feet	3429	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_HARN_StatePlane_Nevada_ West_FIPS_2703	2822	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_HARN_StatePlane_Nevada_ West_FIPS_2703_Feet	3431	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_HARN_StatePlane_New_ Hampshire_FIPS_2800	2823	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_HARN_StatePlane_New_ Hampshire_FIPS_2800_Feet	3445	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_HARN_StatePlane_New_ Jersey_FIPS_2900	2824	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_HARN_StatePlane_New_ Jersey_FIPS_2900_Feet	3432	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_HARN_StatePlane_New_ Mexico_Central_FIPS_3002	2826	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_HARN_StatePlane_New_ Mexico_Central_FIPS_3002_Feet	2903	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_HARN_StatePlane_New_ Mexico_East_FIPS_3001	2825	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_HARN_StatePlane_New_ Mexico_East_FIPS_3001_Feet	2902	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_HARN_StatePlane_New_ Mexico_West_FIPS_3003	2827	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_HARN_StatePlane_New_ Mexico_West_FIPS_3003_Feet	2904	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_HARN_StatePlane_New_York _Central_FIPS_3102	2829	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_HARN_StatePlane_New_York _Central_FIPS_3102_Feet	2906	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_HARN_StatePlane_New_York _East_FIPS_3101	2828	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_HARN_StatePlane_New_York _East_FIPS_3101_Feet	2905	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_HARN_StatePlane_New_York _Long_Island_FIPS_3104	2831	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_HARN_StatePlane_New_York _Long_Island_FIPS_3104_Feet	2908	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_HARN_StatePlane_New_York _West_FIPS_3103	2830	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_HARN_StatePlane_New_York _West_FIPS_3103_Feet	2907	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_HARN_StatePlane_North_ Carolina_FIPS_3200	3358	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_HARN_StatePlane_North_ Carolina_FIPS_3200_Feet	3404	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_HARN_StatePlane_North_ Dakota_North_FIPS_3301	2832	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_HARN_StatePlane_North_ Dakota_North_FIPS_3301_Feet_Intl	2909	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_HARN_StatePlane_North_ Dakota_South_FIPS_3302	2833	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_HARN_StatePlane_North_ Dakota_South_FIPS_3302_Feet_Intl	2910	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_HARN_StatePlane_Ohio_ North_FIPS_3401	2834	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_HARN_StatePlane_Ohio_ North_FIPS_3401_Feet	3753	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_HARN_StatePlane_Ohio_ South_FIPS_3402	2835	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_HARN_StatePlane_Ohio_ South_FIPS_3402_Feet	3754	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_HARN_StatePlane_Oklahoma _North_FIPS_3501	2836	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_HARN_StatePlane_Oklahoma _North_FIPS_3501_Feet	2911	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_HARN_StatePlane_Oklahoma _South_FIPS_3502	2837	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_HARN_StatePlane_Oklahoma _South_FIPS_3502_Feet	2912	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_HARN_StatePlane_Oregon_ North_FIPS_3601	2838	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_HARN_StatePlane_Oregon_ North_FIPS_3601_Feet_Intl	2913	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_HARN_StatePlane_Oregon_ South_FIPS_3602	2839	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_HARN_StatePlane_Oregon_ South_FIPS_3602_Feet_Intl	2914	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_HARN_StatePlane_ Pennsylvania_North_FIPS_3701	3362	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_HARN_StatePlane_ Pennsylvania_North_FIPS_3701_Feet	3363	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_HARN_StatePlane_ Pennsylvania_South_FIPS_3702	3364	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_HARN_StatePlane_ Pennsylvania_South_FIPS_3702_Feet	3365	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_HARN_StatePlane_Puerto_ Rico_Virgin_Islands_FIPS_5200	2866	Caribbean - Puerto Rico and US Virgin Islands - onshore	17.62	-67.97	18.57	-64.51
NAD_1983_HARN_StatePlane_Rhode_ Island_FIPS_3800	2840	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_HARN_StatePlane_Rhode_ Island_FIPS_3800_Feet	3446	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_HARN_StatePlane_South_ Carolina_FIPS_3900	3360	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_HARN_StatePlane_South_ Carolina_FIPS_3900_Feet_Intl	3361	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_HARN_StatePlane_South_ Dakota_North_FIPS_4001	2841	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_HARN_StatePlane_South_ Dakota_North_FIPS_4001_Feet	3458	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_HARN_StatePlane_South_ Dakota_South_FIPS_4002	2842	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_HARN_StatePlane_South_ Dakota_South_FIPS_4002_Feet	3459	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_HARN_StatePlane_Tennessee _FIPS_4100	2843	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_HARN_StatePlane_Tennessee _FIPS_4100_Feet	2915	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_HARN_StatePlane_Texas_ Central_FIPS_4203	2846	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_HARN_StatePlane_Texas_ Central_FIPS_4203_Feet	2918	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_HARN_StatePlane_Texas_ North_Central_FIPS_4202	2845	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_HARN_StatePlane_Texas_ North_Central_FIPS_4202_Feet	2917	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_HARN_StatePlane_Texas_ North_FIPS_4201	2844	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_HARN_StatePlane_Texas_ North_FIPS_4201_Feet	2916	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_HARN_StatePlane_Texas_ South_Central_FIPS_4204	2847	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_HARN_StatePlane_Texas_ South_Central_FIPS_4204_Feet	2919	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_HARN_StatePlane_Texas_ South_FIPS_4205	2848	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_HARN_StatePlane_Texas_ South_FIPS_4205_Feet	2920	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_HARN_StatePlane_Utah_ Central_FIPS_4302	2850	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_HARN_StatePlane_Utah_ Central_FIPS_4302_Feet	3569	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_HARN_StatePlane_Utah_ Central_FIPS_4302_Feet_Intl	2922	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_HARN_StatePlane_Utah_ North_FIPS_4301	2849	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_HARN_StatePlane_Utah_ North_FIPS_4301_Feet	3568	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_HARN_StatePlane_Utah_ North_FIPS_4301_Feet_Intl	2921	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_HARN_StatePlane_Utah_ South_FIPS_4303	2851	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_HARN_StatePlane_Utah_ South_FIPS_4303_Feet	3570	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_HARN_StatePlane_Utah_ South_FIPS_4303_Feet_Intl	2923	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_HARN_StatePlane_Vermont_ FIPS_4400	2852	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_HARN_StatePlane_Vermont_ FIPS_4400_Ft_US	5654	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_HARN_StatePlane_Virginia_ North_FIPS_4501	2853	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_HARN_StatePlane_Virginia_ North_FIPS_4501_Feet	2924	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_HARN_StatePlane_Virginia_ South_FIPS_4502	2854	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_HARN_StatePlane_Virginia_ South_FIPS_4502_Feet	2925	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_HARN_StatePlane_ Washington_North_FIPS_4601	2855	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_HARN_StatePlane_ Washington_North_FIPS_4601_Feet	2926	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_HARN_StatePlane_ Washington_South_FIPS_4602	2856	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_HARN_StatePlane_ Washington_South_FIPS_4602_Feet	2927	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_HARN_StatePlane_West_ Virginia_North_FIPS_4701	2857	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_HARN_StatePlane_West_ Virginia_North_FIPS_4701_Feet	26861	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_HARN_StatePlane_West_ Virginia_South_FIPS_4702	2858	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_HARN_StatePlane_West_ Virginia_South_FIPS_4702_Feet	26862	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_HARN_StatePlane_Wisconsin _Central_FIPS_4802	2860	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_HARN_StatePlane_Wisconsin _Central_FIPS_4802_Feet	2929	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_HARN_StatePlane_Wisconsin _North_FIPS_4801	2859	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_HARN_StatePlane_Wisconsin _North_FIPS_4801_Feet	2928	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_HARN_StatePlane_Wisconsin _South_FIPS_4803	2861	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_HARN_StatePlane_Wisconsin _South_FIPS_4803_Feet	2930	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_HARN_StatePlane_Wyoming_ East_Central_FIPS_4902	2863	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_HARN_StatePlane_Wyoming_ East_Central_FIPS_4902_Feet	3756	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_HARN_StatePlane_Wyoming_ East_FIPS_4901	2862	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_HARN_StatePlane_Wyoming_ East_FIPS_4901_Feet	3755	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_HARN_StatePlane_Wyoming_ West_Central_FIPS_4903	2864	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_HARN_StatePlane_Wyoming_ West_Central_FIPS_4903_Feet	3757	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_HARN_StatePlane_Wyoming_ West_FIPS_4904	2865	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_HARN_StatePlane_Wyoming_ West_FIPS_4904_Feet	3758	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_HARN_Texas_Centric_ Mapping_System_Albers	3085	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_HARN_Texas_Centric_ Mapping_System_Lambert	3084	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_HARN_UTM_Zone_10N	3740	USA - 126°W to 120°W onshore	33.85	-124.79	49.05	-119.99
NAD_1983_HARN_UTM_Zone_11N	3741	USA - 120°W to 114°W onshore	32.26	-120	49.01	-114
NAD_1983_HARN_UTM_Zone_12N	3742	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1983_HARN_UTM_Zone_13N	3743	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1983_HARN_UTM_Zone_14N	3744	USA - 102°W to 96°W onshore	25.83	-102	49.01	-95.99
NAD_1983_HARN_UTM_Zone_15N	3745	USA - 96°W to 90°W onshore	28.42	-96	49.38	-89.99
NAD_1983_HARN_UTM_Zone_16N	3746	USA - 90°W to 84°W onshore	28.85	-90	48.32	-83.99
NAD_1983_HARN_UTM_Zone_17N	3747	USA - 84°W to 78°W onshore	24.41	-84.01	46.13	-78
NAD_1983_HARN_UTM_Zone_18N	3748	USA - 78°W to 72°W onshore	33.84	-78	45.03	-72
NAD_1983_HARN_UTM_Zone_19N	3749	USA - 72°W to 66°W onshore	40.96	-72	47.47	-66.91
NAD_1983_HARN_UTM_Zone_2S	2195	American Samoa - 2 main island groups and Rose Island	-14.59	-170.88	-14.11	-168.09
NAD_1983_HARN_UTM_Zone_4N	3750	USA - 162°W to 156°W onshore - HI	19.51	-160.3	22.29	-156
NAD_1983_HARN_UTM_Zone_5N	3751	USA - 156°W to 150°W onshore - HI	18.87	-156	20.86	-154.74
NAD_1983_HARN_Virginia_Lambert	3969	USA - Virginia	36.54	-83.68	39.46	-75.31
NAD_1983_HARN_Wisconsin_TM	3071	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_Wisconsin_TM_US_Ft	102220	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Adams_ County_Feet	103400	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Adams_ County_Meters	103300	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Adams_and_J uneau_Feet	8226	USA - Wisconsin - Adams and Juneau	43.64	-90.32	44.25	-89.59
NAD_1983_HARN_WISCRS_Adams_and_J uneau_Meters	8225	USA - Wisconsin - Adams and Juneau	43.64	-90.32	44.25	-89.59
NAD_1983_HARN_WISCRS_Ashland_ County_Feet	8224	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Ashland_ County_Meters	8222	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Barron_ County_Feet	8220	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Barron_ County_Meters	8218	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Bayfield_ County_Feet	8216	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Bayfield_ County_Meters	8214	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Brown_ County_Feet	8213	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Brown_ County_Meters	8212	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Buffalo_ County_Feet	8210	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Buffalo_ County_Meters	8209	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Burnett_ County_Feet	8208	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Burnett_ County_Meters	8207	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Calumet_ County_Feet	103407	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Calumet_ County_Meters	103307	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Calumet_Fon d_du_Lac_Outagamie_and_Winnebago_ Feet	8206	USA - Wisconsin - Calumet, Fond du Lac, Outagamie and Winnebago	43.54	-88.89	44.6	-88.04
NAD_1983_HARN_WISCRS_Calumet_Fon d_du_Lac_Outagamie_and_Winnebago_ Meters	8205	USA - Wisconsin - Calumet, Fond du Lac, Outagamie and Winnebago	43.54	-88.89	44.6	-88.04
NAD_1983_HARN_WISCRS_Chippewa_ County_Feet	8204	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Chippewa_ County_Meters	8203	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Clark_County _Feet	8202	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Clark_County _Meters	8201	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Columbia_ County_Feet	8200	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Columbia_ County_Meters	8198	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Crawford_ County_Feet	8197	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Crawford_ County_Meters	8196	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dane_County _Feet	8193	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dane_County _Meters	8191	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dodge_ County_Feet	103413	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dodge_ County_Meters	103313	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dodge_and_ Jefferson_Feet	8189	USA - Wisconsin - Dodge and Jefferson	42.84	-89.02	43.64	-88.4
NAD_1983_HARN_WISCRS_Dodge_and_ Jefferson_Meters	8187	USA - Wisconsin - Dodge and Jefferson	42.84	-89.02	43.64	-88.4
NAD_1983_HARN_WISCRS_Door_County _Feet	8185	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Door_County _Meters	8184	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Douglas_ County_Feet	8182	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Douglas_ County_Meters	8181	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dunn_County _Feet	8180	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Dunn_County _Meters	8179	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_EauClaire_ County_Feet	8093	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_EauClaire_ County_Meters	8092	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Florence_ County_Feet	8091	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Florence_ County_Meters	8090	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Fond_du_Lac _County_Feet	103419	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Fond_du_Lac _County_Meters	103319	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Forest_ County_Feet	8177	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Forest_ County_Meters	8173	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Grant_County _Feet	103421	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Grant_County _Meters	103321	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Green_ County_Feet	103422	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Green_ County_Meters	103322	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Green_and_L afayette_Feet	8170	USA - Wisconsin - Green and Lafayette	42.5	-90.43	42.86	-89.36
NAD_1983_HARN_WISCRS_Green_and_L afayette_Meters	8169	USA - Wisconsin - Green and Lafayette	42.5	-90.43	42.86	-89.36
NAD_1983_HARN_WISCRS_GreenLake_ County_Feet	103423	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_GreenLake_ County_Meters	103323	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Green_Lake_ and_Marquette_Feet	8168	USA - Wisconsin - Green Lake and Marquette	43.63	-89.6	43.99	-88.88
NAD_1983_HARN_WISCRS_Green_Lake_ and_Marquette_Meters	8167	USA - Wisconsin - Green Lake and Marquette	43.63	-89.6	43.99	-88.88
NAD_1983_HARN_WISCRS_Iowa_County _Feet	8166	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Iowa_County _Meters	8165	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Iron_County_ Feet	8164	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Iron_County_ Meters	8163	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Jackson_ County_Feet	8162	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Jackson_ County_Meters	8161	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Jefferson_ County_Feet	103427	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Jefferson_ County_Meters	103327	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Juneau_ County_Feet	103428	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Juneau_ County_Meters	103328	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Kenosha_ County_Feet	103429	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Kenosha_ County_Meters	103329	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Kenosha_Mil waukee_Ozaukee_and_Racine_Feet	8160	USA - Wisconsin - Kenosha, Milwaukee, Ozaukee and Racine	42.49	-88.31	43.55	-87.75
NAD_1983_HARN_WISCRS_Kenosha_Mil waukee_Ozaukee_and_Racine_Meters	8159	USA - Wisconsin - Kenosha, Milwaukee, Ozaukee and Racine	42.49	-88.31	43.55	-87.75
NAD_1983_HARN_WISCRS_Kewaunee_ County_Feet	103430	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Kewaunee_ County_Meters	103330	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Kewaunee_M anitowoc_and_Sheboygan_Feet	8158	USA - Wisconsin - Kewaunee, Manitowoc and Sheboygan	43.54	-88.17	44.68	-87.37
NAD_1983_HARN_WISCRS_Kewaunee_M anitowoc_and_Sheboygan_Meters	8157	USA - Wisconsin - Kewaunee, Manitowoc and Sheboygan	43.54	-88.17	44.68	-87.37
NAD_1983_HARN_WISCRS_LaCrosse_ County_Feet	8156	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_LaCrosse_ County_Meters	8155	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Lafayette_ County_Feet	103432	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Lafayette_ County_Meters	103332	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Langlade_ County_Feet	8154	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Langlade_ County_Meters	8153	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Lincoln_ County_Feet	8152	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Lincoln_ County_Meters	8151	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Manitowoc_ County_Feet	103435	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Manitowoc_ County_Meters	103335	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marathon_ County_Feet	8150	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marathon_ County_Meters	8149	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marinette_ County_Feet	8148	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marinette_ County_Meters	8147	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marquette_ County_Feet	103438	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Marquette_ County_Meters	103338	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Menominee_ County_Feet	8146	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Menominee_ County_Meters	8145	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Milwaukee_ County_Feet	103440	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Milwaukee_ County_Meters	103340	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Monroe_ County_Feet	8144	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Monroe_ County_Meters	8143	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Oconto_ County_Feet	8142	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Oconto_ County_Meters	8141	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Oneida_ County_Feet	8140	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Oneida_ County_Meters	8139	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Outagamie_ County_Feet	103444	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Outagamie_ County_Meters	103344	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Ozaukee_ County_Feet	103445	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Ozaukee_ County_Meters	103345	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Pepin_County _Feet	103446	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Pepin_County _Meters	103346	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Pepin_and_ Pierce_Feet	8138	USA - Wisconsin - Pepin and Pierce	44.4	-92.81	44.87	-91.65
NAD_1983_HARN_WISCRS_Pepin_and_ Pierce_Meters	8137	USA - Wisconsin - Pepin and Pierce	44.4	-92.81	44.87	-91.65
NAD_1983_HARN_WISCRS_Pierce_ County_Feet	103447	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Pierce_ County_Meters	103347	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Polk_County_ Feet	8136	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Polk_County_ Meters	8135	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Portage_ County_Feet	8134	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Portage_ County_Meters	8133	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Price_County _Feet	8132	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Price_County _Meters	8131	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Racine_ County_Feet	103451	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Racine_ County_Meters	103351	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Richland_ County_Feet	8130	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Richland_ County_Meters	8129	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Rock_County _Feet	8128	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Rock_County _Meters	8127	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Rusk_County _Feet	8126	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Rusk_County _Meters	8125	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sauk_County _Feet	8124	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sauk_County _Meters	8123	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sawyer_ County_Feet	8122	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sawyer_ County_Meters	8121	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Shawano_ County_Feet	8120	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Shawano_ County_Meters	8119	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sheboygan_ County_Feet	103458	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Sheboygan_ County_Meters	103358	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_St_Croix_ County_Feet	8118	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_St_Croix_ County_Meters	8117	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Taylor_ County_Feet	8116	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Taylor_ County_Meters	8115	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Trempealeau _County_Feet	8114	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Trempealeau _County_Meters	8113	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Vernon_ County_Feet	8112	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Vernon_ County_Meters	8111	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Vilas_County _Feet	8110	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Vilas_County _Meters	8109	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Walworth_ County_Feet	8108	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Walworth_ County_Meters	8107	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Washburn_ County_Feet	8106	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Washburn_ County_Meters	8105	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Washington_ County_Feet	8104	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Washington_ County_Meters	8103	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waukesha_ County_Feet	8102	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waukesha_ County_Meters	8101	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waupaca_ County_Feet	8100	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waupaca_ County_Meters	8099	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waushara_ County_Feet	8098	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Waushara_ County_Meters	8097	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Winnebago_ County_Feet	103470	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Winnebago_ County_Meters	103370	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Wood_ County_Feet	8096	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_HARN_WISCRS_Wood_ County_Meters	8095	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_Idaho-Ada_County	102459	Idaho - Ada County	43	-116.6	43.85	-115.94
NAD_1983_Idaho_TM	8826	USA - Idaho	41.98	-117.3	49.02	-111
NAD_1983_2011_ICS_Aurora_(US_Feet)	102901	Illinois - Aurora	41.45	-88.95	42.5	-88.19
NAD_1983_2011_ICS_Belleville_(US_ Feet)	102929	Illinois - Belleville	38.08	-90.38	39.01	-89.59
NAD_1983_2011_ICS_Bloomington_(US_ Feet)	102914	Illinois - Bloomington	40.28	-89.27	40.76	-88.45
NAD_1983_2011_ICS_Carbondale_(US_ Feet)	102932	Illinois - Carbondale	37.56	-90.21	38.26	-87.91
NAD_1983_2011_ICS_Carlinville_(US_ Feet)	102925	Illinois - Carlinville	38.99	-90.63	39.53	-89.69
NAD_1983_2011_ICS_Champaign_(US_ Feet)	102916	Illinois - Champaign	39.86	-88.47	40.5	-87.52
NAD_1983_2011_ICS_Charleston_(US_ Feet)	102924	Illinois - Charleston	39.37	-88.48	39.89	-87.53
NAD_1983_2011_ICS_Chicago_(US_Feet)	102903	Illinois - Chicago	41.46	-88.27	42.5	-87.52
NAD_1983_2011_ICS_Decatur_(US_Feet)	102917	Illinois - Decatur	39.21	-89.22	40.29	-88.46
NAD_1983_2011_ICS_Effingham_(US_ Feet)	102928	Illinois - Effingham	38.73	-89.64	39.22	-88.36
NAD_1983_2011_ICS_Eureka_(US_Feet)	102909	Illinois - Eureka	40.59	-89.64	41.15	-88.92
NAD_1983_2011_ICS_Freeport_(US_ Feet)	102902	Illinois - Freeport	41.92	-90.66	42.51	-89.39
NAD_1983_2011_ICS_Galesburg_(US_ Feet)	102915	Illinois - Galesburg	40.18	-90.46	41.24	-89.63
NAD_1983_2011_ICS_Jacksonville_(US_ Feet)	102922	Illinois - Jacksonville	39.39	-91.38	39.88	-89.92
NAD_1983_2011_ICS_Jerseyville_(US_ Feet)	102927	Illinois - Jerseyville	38.86	-90.94	39.41	-90.14
NAD_1983_2011_ICS_Joliet_(US_Feet)	102908	Illinois - Joliet	40.99	-88.27	41.73	-87.52
NAD_1983_2011_ICS_Lincoln_(US_Feet)	102919	Illinois - Lincoln	39.87	-90.59	40.44	-89.14
NAD_1983_2011_ICS_Macomb_(US_ Feet)	102920	Illinois - Macomb	39.83	-90.92	40.64	-90.18
NAD_1983_2011_ICS_Metropolis_(US_ Feet)	102933	Illinois - Metropolis	36.97	-89.53	37.61	-88.05
NAD_1983_2011_ICS_Moline_(US_Feet)	102905	Illinois - Moline	41.32	-91.08	41.79	-90.15
NAD_1983_2011_ICS_Monmouth_(US_ Feet)	102911	Illinois - Monmouth	40.62	-91.19	41.34	-90.43
NAD_1983_2011_ICS_Mount_Vernon_ (US_Feet)	102931	Illinois - Mount Vernon	38.12	-89.71	38.83	-88.69
NAD_1983_2011_ICS_Olney_(US_Feet)	102930	Illinois - Olney	38.23	-88.71	38.92	-87.49
NAD_1983_2011_ICS_Ottawa_(US_Feet)	102906	Illinois - Ottawa	40.92	-89.87	41.64	-88.24
NAD_1983_2011_ICS_Peoria_(US_Feet)	102913	Illinois - Peoria	40.31	-90.01	40.98	-89.26
NAD_1983_2011_ICS_Pontiac_(US_Feet)	102910	Illinois - Pontiac	40.61	-88.94	41.12	-88.23
NAD_1983_2011_ICS_Quincy_(US_Feet)	102918	Illinois - Quincy	39.75	-91.52	40.64	-90.9
NAD_1983_2011_ICS_Robinson_(US_ Feet)	102926	Illinois - Robinson	38.84	-88.48	39.49	-87.51
NAD_1983_2011_ICS_Rockford_(US_ Feet)	102904	Illinois - Rockford	41.58	-89.69	42.51	-88.93
NAD_1983_2011_ICS_Springfield_(US_ Feet)	102921	Illinois - Springfield	39.52	-90.01	39.98	-89.21
NAD_1983_2011_ICS_Sterling _(US_Feet)	102907	Illinois - Sterling	41.14	-90.44	41.94	-89.62
NAD_1983_2011_ICS_Taylorville_(US_ Feet)	102923	Illinois - Taylorville	38.99	-89.71	39.83	-89.02
NAD_1983_2011_ICS_Watseka_(US_ Feet)	102912	Illinois - Watseka	40.39	-88.47	41.02	-87.52
NAD_1983_Kansas_LCC	6922	USA - Kansas	36.99	-102.06	40.01	-94.58
NAD_1983_Kansas_LCC_ftUS	6923	USA - Kansas	36.99	-102.06	40.01	-94.58
NAD_1983_MA11_Guam_Map_Grid	6637	Guam - onshore	13.18	144.58	13.7	145.01
NAD_1983_MA11_UTM_Zone_54N	8692	Pacific - Guam and NMI west of 144°E	10.95	141.19	23.9	144.01
NAD_1983_MA11_UTM_Zone_55N	8693	Pacific - Guam and NMI east of 144°E	11.05	144	23.9	149.55
NAD_1983_Maine_2000_Central_Zone	3463	USA - Maine - CS2000 - C	43.75	-70.03	47.47	-68.33
NAD_1983_Maine_2000_East_Zone	3072	USA - Maine - CS2000 - E	44.18	-68.58	47.37	-66.91
NAD_1983_Maine_2000_West_Zone	3074	USA - Maine - CS2000 - W	43.07	-71.09	46.58	-69.61
NAD_1983_Michigan_GeoRef_Feet_US	102121	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1983_Michigan_GeoRef_Meters	3078	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1983_Mississippi_TM	3814	USA - Mississippi	30.01	-91.65	35.01	-88.09
NAD_1983_MTM_1	32181	Canada - Newfoundland - east of 54.5°W	46.56	-54.5	49.89	-52.54
NAD_1983_MTM_10	32190	Canada - Quebec and Ontario - MTM zone 10	42.26	-81	62.45	-78
NAD_1983_MTM_11	32191	Canada - Ontario - MTM zone 11	41.67	-83.6	46	-81
NAD_1983_MTM_12	32192	Canada - Ontario - MTM zone 12	46	-82.5	55.21	-79.5
NAD_1983_MTM_13	32193	Canada - Ontario - MTM zone 13	46	-85.5	55.59	-82.5
NAD_1983_MTM_14	32194	Canada - Ontario - 88.5°W to 85.5°W	47.17	-88.5	56.7	-85.5
NAD_1983_MTM_15	32195	Canada - Ontario - 91.5°W to 88.5°W	47.97	-91.5	56.9	-88.5
NAD_1983_MTM_16	32196	Canada - Ontario - 94.5°W to 91.5°W	48.06	-94.5	55.2	-91.5
NAD_1983_MTM_17	32197	Canada - Ontario - west of 94.5°W	48.69	-95.16	53.24	-94.5
NAD_1983_MTM_2	32182	Canada - Newfoundland and Labrador - 57.5°W to 54.5°W	46.81	-57.5	54.71	-54.5
NAD_1983_MTM_2_SCoPQ	32180	Canada - Quebec - east of 57°W	46.6	-57	53.76	-54
NAD_1983_MTM_3	32183	Canada - Quebec, Newfoundland and Labrador - MTM zone 3	47.5	-60	55.38	-57.1
NAD_1983_MTM_4	32184	Canada - Quebec and Labrador - 63°W to 60°W	47.16	-63	58.92	-60
NAD_1983_MTM_5	32185	Canada - Quebec and Labrador - 66°W to 63°W	47.95	-66	60.52	-63
NAD_1983_MTM_6	32186	Canada - Quebec and Labrador - 69°W to 66°W	47.31	-69	59	-66
NAD_1983_MTM_7	32187	Canada - Quebec - 72°W to 69°W	45.01	-72	61.8	-69
NAD_1983_MTM_8	32188	Canada - Quebec and Ontario - 75°W to 72°W	44.98	-75	62.53	-72
NAD_1983_MTM_9	32189	Canada - Quebec and Ontario - 78°W to 75°W	43.63	-78	62.65	-75
NAD_1983_MTQ_Lambert	3798	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_NCRS_Las_Vegas_(ftUS)	8380	USA - Nevada - Las Vegas	35.89	-115.5	36.43	-114.72
NAD_1983_NCRS_Las_Vegas_high_(ftUS)	8382	USA - Nevada - Las Vegas high elevation	35.89	-115.5	36.43	-114.72
NAD_1983_NCRS_Las_Vegas_high_(m)	8381	USA - Nevada - Las Vegas high elevation	35.89	-115.5	36.43	-114.72
NAD_1983_NCRS_Las_Vegas_(m)	8379	USA - Nevada - Las Vegas	35.89	-115.5	36.43	-114.72
NAD_1983_Nebraska_Lancaster_County_ FtUS	102705	US - Nebraska - Lancaster County	40.5	-96.93	41.07	-96.43
NAD_1983_Northwest_Territories_ Lambert	3580	Canada - NWT	59.98	-136.46	78.81	-102
NAD_1983_NSRS2007_Alaska_Albers	3467	USA - Alaska	51.3	172.42	71.4	-129.99
NAD_1983_NSRS2007_California_Teale_ Albers	3488	USA - California	32.53	-124.45	42.01	-114.12
NAD_1983_NSRS2007_Contiguous_USA_ Albers	5072	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
NAD_1983_NSRS2007_EPSG_Arctic_zone _5-29	6094	Arctic - 74°30'N to 69°30'N, 173°W to 153°W	69.5	-173	74.51	-153
NAD_1983_NSRS2007_EPSG_Arctic_zone _5-31	6095	Arctic - 74°30'N to 69°30'N, 157°W to 137°W	69.5	-157	74.51	-137
NAD_1983_NSRS2007_EPSG_Arctic_zone _6-14	6096	Arctic - 71°10'N to 66°10'N, 174°W to 156°W	66.16	-174	71.17	-156
NAD_1983_NSRS2007_EPSG_Arctic_zone _6-16	6097	Arctic - 71°10'N to 66°10'N, 156°W to 138°W	66.16	-156	71.17	-138
NAD_1983_NSRS2007_Florida_GDL_ Albers	3513	USA - Florida	24.41	-87.63	31.01	-79.97
NAD_1983_NSRS2007_Maine_2000_ Central_Zone	3554	USA - Maine - CS2000 - C	43.75	-70.03	47.47	-68.33
NAD_1983_NSRS2007_Maine_2000_ East_Zone	3555	USA - Maine - CS2000 - E	44.18	-68.58	47.37	-66.91
NAD_1983_NSRS2007_Maine_2000_ West_Zone	3556	USA - Maine - CS2000 - W	43.07	-71.09	46.58	-69.61
NAD_1983_NSRS2007_Michigan_GeoRef _Meters	3591	USA - Michigan	41.69	-90.42	48.32	-82.13
NAD_1983_NSRS2007_Mississippi_TM	3816	USA - Mississippi	30.01	-91.65	35.01	-88.09
NAD_1983_ NSRS2007_Navajo_Nation_ Coordinate_System_Meters	103589	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_ NSRS2007_Navajo_Nation_ Coordinate_System_US_Feet	103590	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_ NSRS2007_Navajo_Nation_ Coordinate_System_Intl_Feet	103591	Navajo Nation	32.8	-114.04	37.75	-106.17
NAD_1983_NSRS2007_Oregon_Statewide _Lambert	3643	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_NSRS2007_Oregon_Statewide _Lambert_Ft_Intl	3644	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_NSRS2007_StatePlane_ Alabama_East_FIPS_0101	3465	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_NSRS2007_StatePlane_ Alabama_West_FIPS_0102	3466	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_NSRS2007_StatePlane_Alaska _10_FIPS_5010	3477	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_NSRS2007_StatePlane_Alaska _1_FIPS_5001	3468	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_NSRS2007_StatePlane_Alaska _2_FIPS_5002	3469	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_NSRS2007_StatePlane_Alaska _3_FIPS_5003	3470	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_NSRS2007_StatePlane_Alaska _4_FIPS_5004	3471	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_NSRS2007_StatePlane_Alaska _5_FIPS_5005	3472	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_NSRS2007_StatePlane_Alaska _6_FIPS_5006	3473	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_NSRS2007_StatePlane_Alaska _7_FIPS_5007	3474	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_NSRS2007_StatePlane_Alaska _8_FIPS_5008	3475	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_NSRS2007_StatePlane_Alaska _9_FIPS_5009	3476	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_NSRS2007_StatePlane_ Arizona_Central_FIPS_0202	3478	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_NSRS2007_StatePlane_ Arizona_Central_FIPS_0202_Ft_Intl	3479	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_NSRS2007_StatePlane_ Arizona_East_FIPS_0201	3480	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_NSRS2007_StatePlane_ Arizona_East_FIPS_0201_Ft_Intl	3481	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_NSRS2007_StatePlane_ Arizona_West_FIPS_0203	3482	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_NSRS2007_StatePlane_ Arizona_West_FIPS_0203_Ft_Intl	3483	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_NSRS2007_StatePlane_ Arkansas_North_FIPS_0301	3484	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_NSRS2007_StatePlane_ Arkansas_North_FIPS_0301_Ft_US	3485	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_NSRS2007_StatePlane_ Arkansas_South_FIPS_0302	3486	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_NSRS2007_StatePlane_ Arkansas_South_FIPS_0302_Ft_US	3487	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_NSRS2007_StatePlane_ California_I_FIPS_0401	3489	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_NSRS2007_StatePlane_ California_I_FIPS_0401_Ft_US	3490	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_NSRS2007_StatePlane_ California_II_FIPS_0402	3491	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_NSRS2007_StatePlane_ California_II_FIPS_0402_Ft_US	3492	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_NSRS2007_StatePlane_ California_III_FIPS_0403	3493	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_NSRS2007_StatePlane_ California_III_FIPS_0403_Ft_US	3494	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_NSRS2007_StatePlane_ California_IV_FIPS_0404	3495	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_NSRS2007_StatePlane_ California_IV_FIPS_0404_Ft_US	3496	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_NSRS2007_StatePlane_ California_V_FIPS_0405	3497	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_NSRS2007_StatePlane_ California_V_FIPS_0405_Ft_US	3498	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_NSRS2007_StatePlane_ California_VI_FIPS_0406	3499	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_NSRS2007_StatePlane_ California_VI_FIPS_0406_Ft_US	3500	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_NSRS2007_StatePlane_ Colorado_Central_FIPS_0502	3501	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_NSRS2007_StatePlane_ Colorado_Central_FIPS_0502_Ft_US	3502	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_NSRS2007_StatePlane_ Colorado_North_FIPS_0501	3503	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_NSRS2007_StatePlane_ Colorado_North_FIPS_0501_Ft_US	3504	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_NSRS2007_StatePlane_ Colorado_South_FIPS_0503	3505	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_NSRS2007_StatePlane_ Colorado_South_FIPS_0503_Ft_US	3506	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_NSRS2007_StatePlane_ Connecticut_FIPS_0600	3507	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_NSRS2007_StatePlane_ Connecticut_FIPS_0600_Ft_US	3508	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_NSRS2007_StatePlane_ Delaware_FIPS_0700	3509	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_NSRS2007_StatePlane_ Delaware_FIPS_0700_Ft_US	3510	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_NSRS2007_StatePlane_ Florida_East_FIPS_0901	3511	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_NSRS2007_StatePlane_ Florida_East_FIPS_0901_Ft_US	3512	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_NSRS2007_StatePlane_ Florida_North_FIPS_0903	3514	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_NSRS2007_StatePlane_ Florida_North_FIPS_0903_Ft_US	3515	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_NSRS2007_StatePlane_ Florida_West_FIPS_0902	3516	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_NSRS2007_StatePlane_ Florida_West_FIPS_0902_Ft_US	3517	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_NSRS2007_StatePlane_ Georgia_East_FIPS_1001	3518	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_NSRS2007_StatePlane_ Georgia_East_FIPS_1001_Ft_US	3519	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_NSRS2007_StatePlane_ Georgia_West_FIPS_1002	3520	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_NSRS2007_StatePlane_ Georgia_West_FIPS_1002_Ft_US	3521	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_NSRS2007_StatePlane_Idaho _Central_FIPS_1102	3522	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_NSRS2007_StatePlane_Idaho _Central_FIPS_1102_Ft_US	3523	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_NSRS2007_StatePlane_Idaho _East_FIPS_1101	3524	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_NSRS2007_StatePlane_Idaho _East_FIPS_1101_Ft_US	3525	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_NSRS2007_StatePlane_Idaho _West_FIPS_1103	3526	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_NSRS2007_StatePlane_Idaho _West_FIPS_1103_Ft_US	3527	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_NSRS2007_StatePlane_Illinois _East_FIPS_1201	3528	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_NSRS2007_StatePlane_Illinois _East_FIPS_1201_Ft_US	3529	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_NSRS2007_StatePlane_Illinois _West_FIPS_1202	3530	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_NSRS2007_StatePlane_Illinois _West_FIPS_1202_Ft_US	3531	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_NSRS2007_StatePlane_ Indiana_East_FIPS_1301	3532	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_NSRS2007_StatePlane_ Indiana_East_FIPS_1301_Ft_US	3533	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_NSRS2007_StatePlane_ Indiana_West_FIPS_1302	3534	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_NSRS2007_StatePlane_ Indiana_West_FIPS_1302_Ft_US	3535	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_NSRS2007_StatePlane_Iowa_ North_FIPS_1401	3536	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_NSRS2007_StatePlane_Iowa_ North_FIPS_1401_Ft_US	3537	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_NSRS2007_StatePlane_Iowa_ South_FIPS_1402	3538	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_NSRS2007_StatePlane_Iowa_ South_FIPS_1402_Ft_US	3539	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_NSRS2007_StatePlane_Kansas _North_FIPS_1501	3540	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_NSRS2007_StatePlane_Kansas _North_FIPS_1501_Ft_US	3541	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_NSRS2007_StatePlane_Kansas _South_FIPS_1502	3542	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_NSRS2007_StatePlane_Kansas _South_FIPS_1502_Ft_US	3543	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_NSRS2007_StatePlane_ Kentucky_FIPS_1600	3546	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_NSRS2007_StatePlane_ Kentucky_FIPS_1600_Ft_US	3547	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_NSRS2007_StatePlane_ Kentucky_North_FIPS_1601	3544	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_NSRS2007_StatePlane_ Kentucky_North_FIPS_1601_Ft_US	3545	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_NSRS2007_StatePlane_ Kentucky_South_FIPS_1602	3548	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_NSRS2007_StatePlane_ Kentucky_South_FIPS_1602_Ft_US	3549	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_NSRS2007_StatePlane_ Louisiana_North_FIPS_1701	3550	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_NSRS2007_StatePlane_ Louisiana_North_FIPS_1701_Ft_US	3551	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_NSRS2007_StatePlane_ Louisiana_South_FIPS_1702	3552	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_NSRS2007_StatePlane_ Louisiana_South_FIPS_1702_Ft_US	3553	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_NSRS2007_StatePlane_Maine _East_FIPS_1801	3557	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_NSRS2007_StatePlane_Maine _East_FIPS_1801_Ft_US	26863	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_NSRS2007_StatePlane_Maine _West_FIPS_1802	3558	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_NSRS2007_StatePlane_Maine _West_FIPS_1802_Ft_US	26864	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_NSRS2007_StatePlane_ Maryland_FIPS_1900	3559	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_NSRS2007_StatePlane_ Maryland_FIPS_1900_Ft_US	3582	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_NSRS2007_StatePlane_ Massachusetts_Island_FIPS_2002	3583	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_NSRS2007_StatePlane_ Massachusetts_Isl_FIPS_2002_FtUS	3584	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_NSRS2007_StatePlane_ Massachusetts_Mainland_FIPS_2001	3585	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_NSRS2007_StatePlane_ Massachusetts_Mnld_FIPS_2001_FtUS	3586	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_NSRS2007_StatePlane_ Michigan_Central_FIPS_2112	3587	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_NSRS2007_StatePlane_ Michigan_Central_FIPS_2112_Ft_Intl	3588	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_NSRS2007_StatePlane_ Michigan_North_FIPS_2111	3589	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_NSRS2007_StatePlane_ Michigan_North_FIPS_2111_Ft_Intl	3590	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_NSRS2007_StatePlane_ Michigan_South_FIPS_2113	3592	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_NSRS2007_StatePlane_ Michigan_South_FIPS_2113_Ft_Intl	3593	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_NSRS2007_StatePlane_ Minnesota_Central_FIPS_2202	3594	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_NSRS2007_StatePlane_ Minnesota_Central_FIPS_2202_Ft_US	26866	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_NSRS2007_StatePlane_ Minnesota_North_FIPS_2201	3595	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_NSRS2007_StatePlane_ Minnesota_North_FIPS_2201_Ft_US	26865	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_NSRS2007_StatePlane_ Minnesota_South_FIPS_2203	3596	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_NSRS2007_StatePlane_ Minnesota_South_FIPS_2203_Ft_US	26867	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_NSRS2007_StatePlane_ Mississippi_East_FIPS_2301	3597	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_NSRS2007_StatePlane_ Mississippi_East_FIPS_2301_Ft_US	3598	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_NSRS2007_StatePlane_ Mississippi_West_FIPS_2302	3599	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_NSRS2007_StatePlane_ Mississippi_West_FIPS_2302_Ft_US	3600	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_NSRS2007_StatePlane_ Missouri_Central_FIPS_2402	3601	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_NSRS2007_StatePlane_ Missouri_East_FIPS_2401	3602	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_NSRS2007_StatePlane_ Missouri_West_FIPS_2403	3603	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_NSRS2007_StatePlane_ Montana_FIPS_2500	3604	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_NSRS2007_StatePlane_ Montana_FIPS_2500_Ft_Intl	3605	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_NSRS2007_StatePlane_ Nebraska_FIPS_2600	3606	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_NSRS2007_StatePlane_ Nebraska_FIPS_2600_Ft_US	26868	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_NSRS2007_StatePlane_ Nevada_Central_FIPS_2702	3607	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_NSRS2007_StatePlane_ Nevada_Central_FIPS_2702_Ft_US	3608	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_NSRS2007_StatePlane_ Nevada_East_FIPS_2701	3609	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_NSRS2007_StatePlane_ Nevada_East_FIPS_2701_Ft_US	3610	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_NSRS2007_StatePlane_ Nevada_West_FIPS_2703	3611	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_NSRS2007_StatePlane_ Nevada_West_FIPS_2703_Ft_US	3612	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_NSRS2007_StatePlane_New_ Hampshire_FIPS_2800	3613	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_NSRS2007_StatePlane_New_ Hampshire_FIPS_2800_Ft_US	3614	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_NSRS2007_StatePlane_New_ Jersey_FIPS_2900	3615	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_NSRS2007_StatePlane_New_ Jersey_FIPS_2900_Ft_US	3616	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_NSRS2007_StatePlane_New_ Mexico_Central_FIPS_3002	3617	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_NSRS2007_StatePlane_New_ Mexico_Central_FIPS_3002_Ft_US	3618	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_NSRS2007_StatePlane_New_ Mexico_East_FIPS_3001	3619	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_NSRS2007_StatePlane_New_ Mexico_East_FIPS_3001_Ft_US	3620	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_NSRS2007_StatePlane_New_ Mexico_West_FIPS_3003	3621	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_NSRS2007_StatePlane_New_ Mexico_West_FIPS_3003_Ft_US	3622	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_NSRS2007_StatePlane_New_ York_Central_FIPS_3102	3623	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_NSRS2007_StatePlane_New_ York_Central_FIPS_3102_Ft_US	3624	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_NSRS2007_StatePlane_New_ York_East_FIPS_3101	3625	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_NSRS2007_StatePlane_New_ York_East_FIPS_3101_Ft_US	3626	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_NSRS2007_StatePlane_New_ York_Long_Island_FIPS_3104	3627	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_NSRS2007_StatePlane_New_ York_Long_Isl_FIPS_3104_Ft_US	3628	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_NSRS2007_StatePlane_New_ York_West_FIPS_3103	3629	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_NSRS2007_StatePlane_New_ York_West_FIPS_3103_Ft_US	3630	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_NSRS2007_StatePlane_North _Carolina_FIPS_3200	3631	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_NSRS2007_StatePlane_North _Carolina_FIPS_3200_Ft_US	3632	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_NSRS2007_StatePlane_North _Dakota_North_FIPS_3301	3633	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_NSRS2007_StatePlane_North _Dakota_North_FIPS_3301_FtI	3634	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_NSRS2007_StatePlane_North _Dakota_South_FIPS_3302	3635	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_NSRS2007_StatePlane_North _Dakota_South_FIPS_3302_FtI	3636	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_NSRS2007_StatePlane_Ohio_ North_FIPS_3401	3637	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_NSRS2007_StatePlane_Ohio_ North_FIPS_3401_Ft_US	3728	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_NSRS2007_StatePlane_Ohio_ South_FIPS_3402	3638	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_NSRS2007_StatePlane_Ohio_ South_FIPS_3402_Ft_US	3729	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_NSRS2007_StatePlane_ Oklahoma_North_FIPS_3501	3639	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_NSRS2007_StatePlane_ Oklahoma_North_FIPS_3501_Ft_US	3640	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_NSRS2007_StatePlane_ Oklahoma_South_FIPS_3502	3641	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_NSRS2007_StatePlane_ Oklahoma_South_FIPS_3502_Ft_US	3642	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_NSRS2007_StatePlane_ Oregon_North_FIPS_3601	3645	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_NSRS2007_StatePlane_ Oregon_North_FIPS_3601_Ft_Intl	3646	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_NSRS2007_StatePlane_ Oregon_South_FIPS_3602	3647	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_NSRS2007_StatePlane_ Oregon_South_FIPS_3602_Ft_Intl	3648	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_NSRS2007_StatePlane_ Pennsylvania_North_FIPS_3701	3649	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_NSRS2007_StatePlane_ Pennsylvania_North_FIPS_3701_Ft_US	3650	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_NSRS2007_StatePlane_ Pennsylvania_South_FIPS_3702	3651	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_NSRS2007_StatePlane_ Pennsylvania_South_FIPS_3702_Ft_US	3652	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_NSRS2007_StatePlane_Puerto _Rico_Virgin_Isls_FIPS_5200	4437	Caribbean - Puerto Rico and US Virgin Islands - onshore	17.62	-67.97	18.57	-64.51
NAD_1983_NSRS2007_StatePlane_Rhode _Island_FIPS_3800	3653	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_NSRS2007_StatePlane_Rhode _Island_FIPS_3800_Ft_US	3654	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_NSRS2007_StatePlane_South _Carolina_FIPS_3900	3655	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_NSRS2007_StatePlane_South _Carolina_FIPS_3900_Ft_Intl	3656	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_NSRS2007_StatePlane_South _Dakota_North_FIPS_4001	3657	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_NSRS2007_StatePlane_South _Dakota_North_FIPS_4001_Ft_US	3658	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_NSRS2007_StatePlane_South _Dakota_South_FIPS_4002	3659	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_NSRS2007_StatePlane_South _Dakota_South_FIPS_4002_Ft_US	3660	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_NSRS2007_StatePlane_ Tennessee_FIPS_4100	3661	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_NSRS2007_StatePlane_ Tennessee_FIPS_4100_Ft_US	3662	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_NSRS2007_StatePlane_Texas_ Central_FIPS_4203	3663	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_NSRS2007_StatePlane_Texas_ Central_FIPS_4203_Ft_US	3664	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_NSRS2007_StatePlane_Texas_ North_Central_FIPS_4202	3669	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_NSRS2007_StatePlane_Texas_ North_Central_FIPS_4202_FtUS	3670	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_NSRS2007_StatePlane_Texas_ North_FIPS_4201	3667	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_NSRS2007_StatePlane_Texas_ North_FIPS_4201_Ft_US	3668	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_NSRS2007_StatePlane_Texas_ South_Central_FIPS_4204	3673	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_NSRS2007_StatePlane_Texas_ South_Central_FIPS_4204_FtUS	3674	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_NSRS2007_StatePlane_Texas_ South_FIPS_4205	3671	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_NSRS2007_StatePlane_Texas_ South_FIPS_4205_Ft_US	3672	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_NSRS2007_StatePlane_Utah_ Central_FIPS_4302	3675	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ Central_FIPS_4302_Ft_Intl	3676	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ Central_FIPS_4302_Ft_US	3677	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ North_FIPS_4301	3678	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ North_FIPS_4301_Ft_Intl	3679	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ North_FIPS_4301_Ft_US	3680	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ South_FIPS_4303	3681	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ South_FIPS_4303_Ft_Intl	3682	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_NSRS2007_StatePlane_Utah_ South_FIPS_4303_Ft_US	3683	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_NSRS2007_StatePlane_ Vermont_FIPS_4400	3684	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_NSRS2007_StatePlane_ Vermont_FIPS_4400_Ft_US	5655	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_NSRS2007_StatePlane_ Virginia_North_FIPS_4501	3685	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_NSRS2007_StatePlane_ Virginia_North_FIPS_4501_Ft_US	3686	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_NSRS2007_StatePlane_ Virginia_South_FIPS_4502	3687	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_NSRS2007_StatePlane_ Virginia_South_FIPS_4502_Ft_US	3688	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_NSRS2007_StatePlane_ Washington_North_FIPS_4601	3689	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_NSRS2007_StatePlane_ Washington_North_FIPS_4601_Ft_US	3690	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_NSRS2007_StatePlane_ Washington_South_FIPS_4602	3691	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_NSRS2007_StatePlane_ Washington_South_FIPS_4602_Ft_US	3692	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_NSRS2007_StatePlane_West_ Virginia_North_FIPS_4701	3693	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_NSRS2007_StatePlane_West_ Virginia_North_FIPS_4701_FtUS	26869	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_NSRS2007_StatePlane_West_ Virginia_South_FIPS_4702	3694	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_NSRS2007_StatePlane_West_ Virginia_South_FIPS_4702_FtUS	26870	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_NSRS2007_StatePlane_ Wisconsin_Central_FIPS_4802	3695	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_NSRS2007_StatePlane_ Wisconsin_Central_FIPS_4802_Ft_US	3696	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_NSRS2007_StatePlane_ Wisconsin_North_FIPS_4801	3697	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_NSRS2007_StatePlane_ Wisconsin_North_FIPS_4801_Ft_US	3698	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_NSRS2007_StatePlane_ Wisconsin_South_FIPS_4803	3699	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_NSRS2007_StatePlane_ Wisconsin_South_FIPS_4803_Ft_US	3700	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_NSRS2007_StatePlane_ Wyoming_East_Central_FIPS_4902	3703	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_NSRS2007_StatePlane_ Wyoming_East_FIPS_4901	3702	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_NSRS2007_StatePlane_ Wyoming_East_FIPS_4901_Ft_US	3730	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_NSRS2007_StatePlane_ Wyoming_E_Central_FIPS_4902_Ft_US	3731	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_NSRS2007_StatePlane_ Wyoming_W_Central_FIPS_4903_Ft_US	3732	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_NSRS2007_StatePlane_ Wyoming_West_Central_FIPS_4903	3704	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_NSRS2007_StatePlane_ Wyoming_West_FIPS_4904	3705	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_NSRS2007_StatePlane_ Wyoming_West_FIPS_4904_Ft_US	3733	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_NSRS2007_Texas_Centric_ Mapping_System_Albers	3665	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_NSRS2007_Texas_Centric_ Mapping_System_Lambert	3666	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_NSRS2007_UTM_Zone_10N	3717	USA - 126°W to 120°W	30.54	-126	49.09	-119.99
NAD_1983_NSRS2007_UTM_Zone_11N	3718	USA - 120°W to 114°W	30.88	-120	49.01	-114
NAD_1983_NSRS2007_UTM_Zone_12N	3719	USA - 114°W to 108°W	31.33	-114	49.01	-108
NAD_1983_NSRS2007_UTM_Zone_13N	3720	USA - 108°W to 102°W	28.98	-108	49.01	-102
NAD_1983_NSRS2007_UTM_Zone_14N	3721	USA - 102°W to 96°W	25.83	-102	49.01	-96
NAD_1983_NSRS2007_UTM_Zone_15N	3722	USA - 96°W to 90°W	25.61	-96.01	49.38	-90
NAD_1983_NSRS2007_UTM_Zone_16N	3723	USA - 90°W to 84°W	23.97	-90	48.32	-84
NAD_1983_NSRS2007_UTM_Zone_17N	3724	USA - 84°W to 78°W	23.81	-84	46.13	-78
NAD_1983_NSRS2007_UTM_Zone_18N	3725	USA - 78°W to 72°W	28.28	-78	45.03	-72
NAD_1983_NSRS2007_UTM_Zone_19N	3726	USA - 72°W to 66°W	33.61	-72	47.47	-65.99
NAD_1983_NSRS2007_UTM_Zone_1N	3708	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1983_NSRS2007_UTM_Zone_20N	102044	Caribbean - Puerto Rico and US Virgin Islands	14.92	-68.49	21.86	-63.88
NAD_1983_NSRS2007_UTM_Zone_2N	3709	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1983_NSRS2007_UTM_Zone_3N	3710	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_NSRS2007_UTM_Zone_4N	3711	USA - 162°W to 156°W - AK, OCS	50.98	-162	74.71	-155.99
NAD_1983_NSRS2007_UTM_Zone_59N	3706	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1983_NSRS2007_UTM_Zone_5N	3712	USA - 156°W to 150°W - AK, OCS	52.15	-156	74.71	-149.99
NAD_1983_NSRS2007_UTM_Zone_60N	3707	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1983_NSRS2007_UTM_Zone_6N	3713	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1983_NSRS2007_UTM_Zone_7N	3714	USA - 144°W to 138°W	53.47	-144	73.59	-137.99
NAD_1983_NSRS2007_UTM_Zone_8N	3715	USA - 138°W to 132°W	53.6	-138	73.04	-131.99
NAD_1983_NSRS2007_UTM_Zone_9N	3716	USA - 132°W to 126°W	35.38	-132	56.84	-126
NAD_1983_NSRS2007_Virginia_Lambert	3970	USA - Virginia	36.54	-83.68	39.46	-75.31
NAD_1983_NSRS2007_Wisconsin_TM	3701	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_NSRS2007_Wisconsin_TM_US _Ft	102217	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_Ontario_MNR_Lambert	3161	Canada - Ontario	41.67	-95.16	56.9	-74.35
NAD_1983_Oregon_Statewide_Lambert	2991	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_Oregon_Statewide_Lambert_ Feet_Intl	2992	USA - Oregon	41.98	-124.6	46.26	-116.47
NAD_1983_PA11_StatePlane_Hawaii_1_ FIPS_5101	6628	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_PA11_StatePlane_Hawaii_1_ FIPS_5101_Feet	102525	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_PA11_StatePlane_Hawaii_2_ FIPS_5102	6629	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_PA11_StatePlane_Hawaii_2_ FIPS_5102_Feet	102526	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_PA11_StatePlane_Hawaii_3_ FIPS_5103	6630	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_PA11_StatePlane_Hawaii_3_ FIPS_5103_Feet	6633	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_PA11_StatePlane_Hawaii_4_ FIPS_5104	6631	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_PA11_StatePlane_Hawaii_4_ FIPS_5104_Feet	102528	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_PA11_StatePlane_Hawaii_5_ FIPS_5105	6632	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_PA11_StatePlane_Hawaii_5_ FIPS_5105_Feet	102529	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_PA11_UTM_Zone_2S	6636	American Samoa - 2 main island groups and Rose Island	-14.59	-170.88	-14.11	-168.09
NAD_1983_PA11_UTM_Zone_4N	6634	USA - 162°W to 156°W onshore - HI	19.51	-160.3	22.29	-156
NAD_1983_PA11_UTM_Zone_5N	6635	USA - 156°W to 150°W onshore - HI	18.87	-156	20.86	-154.74
NAD_1983_PACP00_UTM_Zone_2S	102703	American Samoa - 2 main island groups and Rose Island	-14.59	-170.88	-14.11	-168.09
NAD_1983_PACP00_UTM_Zone_4N	102701	USA - 162°W to 156°W onshore - HI	19.51	-160.3	22.29	-156
NAD_1983_PACP00_UTM_Zone_5N	102702	USA - 156°W to 150°W onshore - HI	18.87	-156	20.86	-154.74
NAD_1983_Quebec_Albers	6623	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_Quebec_Lambert	32198	Canada - Quebec	44.99	-79.85	62.62	-57.1
NAD_1983_StatePlane_Alabama_East_ FIPS_0101	26929	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_StatePlane_Alabama_East_ FIPS_0101_Feet	102629	USA - Alabama - SPCS - E	30.99	-86.79	35	-84.89
NAD_1983_StatePlane_Alabama_West_ FIPS_0102	26930	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_StatePlane_Alabama_West_ FIPS_0102_Feet	102630	USA - Alabama - SPCS - W	30.14	-88.48	35.02	-86.3
NAD_1983_StatePlane_Alaska_10_FIPS_ 5010	26940	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_StatePlane_Alaska_10_FIPS_ 5010_Feet	102640	USA - Alaska - Aleutian Islands	51.3	172.42	54.34	-164.84
NAD_1983_StatePlane_Alaska_1_FIPS_ 5001	26931	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_StatePlane_Alaska_1_FIPS_ 5001_Feet	102631	USA - Alaska - Panhandle	54.61	-141	60.35	-129.99
NAD_1983_StatePlane_Alaska_2_FIPS_ 5002	26932	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_StatePlane_Alaska_2_FIPS_ 5002_Feet	102632	USA - Alaska - 144°W to 141°W	59.72	-144.01	70.16	-140.98
NAD_1983_StatePlane_Alaska_3_FIPS_ 5003	26933	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_StatePlane_Alaska_3_FIPS_ 5003_Feet	102633	USA - Alaska - 148°W to 144°W	59.72	-148	70.38	-144
NAD_1983_StatePlane_Alaska_4_FIPS_ 5004	26934	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_StatePlane_Alaska_4_FIPS_ 5004_Feet	102634	USA - Alaska - 152°W to 148°W	59.11	-152.01	70.63	-147.99
NAD_1983_StatePlane_Alaska_5_FIPS_ 5005	26935	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_StatePlane_Alaska_5_FIPS_ 5005_Feet	102635	USA - Alaska - 156°W to 152°W	55.72	-156	71.28	-151.86
NAD_1983_StatePlane_Alaska_6_FIPS_ 5006	26936	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_StatePlane_Alaska_6_FIPS_ 5006_Feet	102636	USA - Alaska - 160°W to 156°W	54.89	-160	71.4	-155.99
NAD_1983_StatePlane_Alaska_7_FIPS_ 5007	26937	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_StatePlane_Alaska_7_FIPS_ 5007_Feet	102637	USA - Alaska - 164°W to 160°W	54.32	-164.01	70.74	-160
NAD_1983_StatePlane_Alaska_8_FIPS_ 5008	26938	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_StatePlane_Alaska_8_FIPS_ 5008_Feet	102638	USA - Alaska - north of 54.5°N; 168°W to 164°W	54.34	-168.26	69.05	-164
NAD_1983_StatePlane_Alaska_9_FIPS_ 5009	26939	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_StatePlane_Alaska_9_FIPS_ 5009_Feet	102639	USA - Alaska - north of 54.5°N; west of 168°W	56.49	-173.16	65.82	-168
NAD_1983_StatePlane_Arizona_Central_ FIPS_0202	26949	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_StatePlane_Arizona_Central_ FIPS_0202_Feet	102649	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_StatePlane_Arizona_Central_ FIPS_0202_Feet_Intl	2223	USA - Arizona - SPCS - C	31.33	-113.35	37.01	-110.44
NAD_1983_StatePlane_Arizona_East_ FIPS_0201	26948	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_StatePlane_Arizona_East_ FIPS_0201_Feet	102648	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_StatePlane_Arizona_East_ FIPS_0201_Feet_Intl	2222	USA - Arizona - SPCS - E	31.33	-111.71	37.01	-109.04
NAD_1983_StatePlane_Arizona_West_ FIPS_0203	26950	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_StatePlane_Arizona_West_ FIPS_0203_Feet	102650	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_StatePlane_Arizona_West_ FIPS_0203_Feet_Intl	2224	USA - Arizona - SPCS - W	32.05	-114.81	37	-112.52
NAD_1983_StatePlane_Arkansas_North_ FIPS_0301	26951	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_StatePlane_Arkansas_North_ FIPS_0301_Feet	3433	USA - Arkansas - SPCS - N	34.67	-94.62	36.5	-89.64
NAD_1983_StatePlane_Arkansas_South_ FIPS_0302	26952	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_StatePlane_Arkansas_South_ FIPS_0302_Feet	3434	USA - Arkansas - SPCS - S	33.01	-94.48	35.1	-90.4
NAD_1983_StatePlane_California_I_FIPS_ 0401	26941	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_StatePlane_California_I_FIPS_ 0401_Feet	2225	USA - California - SPCS - 1	39.59	-124.45	42.01	-119.99
NAD_1983_StatePlane_California_II_FIPS _0402	26942	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_StatePlane_California_II_FIPS _0402_Feet	2226	USA - California - SPCS - 2	38.02	-124.06	40.16	-119.54
NAD_1983_StatePlane_California_III_FIPS _0403	26943	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_StatePlane_California_III_FIPS _0403_Feet	2227	USA - California - SPCS - 3	36.73	-123.02	38.71	-117.83
NAD_1983_StatePlane_California_IV_FIPS _0404	26944	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_StatePlane_California_IV_FIPS _0404_Feet	2228	USA - California - SPCS - 4	35.78	-122.01	37.58	-115.62
NAD_1983_StatePlane_California_V_FIPS _0405	26945	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_StatePlane_California_V_FIPS _0405_Feet	2229	USA - California - SPCS83 - 5	32.76	-121.42	35.81	-114.12
NAD_1983_StatePlane_California_VI_FIPS _0406	26946	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_StatePlane_California_VI_FIPS _0406_Feet	2230	USA - California - SPCS - 6	32.53	-118.15	34.08	-114.42
NAD_1983_StatePlane_Colorado_Central _FIPS_0502	26954	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_StatePlane_Colorado_Central _FIPS_0502_Feet	2232	USA - Colorado - SPCS - C	38.14	-109.06	40.09	-102.04
NAD_1983_StatePlane_Colorado_North_ FIPS_0501	26953	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_StatePlane_Colorado_North_ FIPS_0501_Feet	2231	USA - Colorado - SPCS - N	39.56	-109.06	41.01	-102.04
NAD_1983_StatePlane_Colorado_South_ FIPS_0503	26955	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_StatePlane_Colorado_South_ FIPS_0503_Feet	2233	USA - Colorado - SPCS - S	36.98	-109.06	38.68	-102.04
NAD_1983_StatePlane_Connecticut_FIPS _0600	26956	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_StatePlane_Connecticut_FIPS _0600_Feet	2234	USA - Connecticut	40.98	-73.73	42.05	-71.78
NAD_1983_StatePlane_Delaware_FIPS_ 0700	26957	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_StatePlane_Delaware_FIPS_ 0700_Feet	2235	USA - Delaware	38.44	-75.8	39.85	-74.97
NAD_1983_StatePlane_Florida_East_FIPS _0901	26958	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_StatePlane_Florida_East_FIPS _0901_Feet	2236	USA - Florida - SPCS - E	24.41	-82.33	30.83	-79.97
NAD_1983_StatePlane_Florida_North_ FIPS_0903	26960	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_StatePlane_Florida_North_ FIPS_0903_Feet	2238	USA - Florida - SPCS - N	29.21	-87.63	31.01	-82.04
NAD_1983_StatePlane_Florida_West_ FIPS_0902	26959	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_StatePlane_Florida_West_ FIPS_0902_Feet	2237	USA - Florida - SPCS - W	26.27	-83.34	29.6	-81.13
NAD_1983_StatePlane_Georgia_East_ FIPS_1001	26966	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_StatePlane_Georgia_East_ FIPS_1001_Feet	2239	USA - Georgia - SPCS - E	30.36	-83.47	34.68	-80.77
NAD_1983_StatePlane_Georgia_West_ FIPS_1002	26967	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_StatePlane_Georgia_West_ FIPS_1002_Feet	2240	USA - Georgia - SPCS - W	30.62	-85.61	35.01	-82.99
NAD_1983_StatePlane_Guam_FIPS_5400	65161	Guam	10.95	141.19	15.91	148.18
NAD_1983_StatePlane_Guam_FIPS_5400 _Feet	102766	Guam	10.95	141.19	15.91	148.18
NAD_1983_StatePlane_Hawaii_1_FIPS_ 5101	26961	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_StatePlane_Hawaii_1_FIPS_ 5101_Feet	102661	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
NAD_1983_StatePlane_Hawaii_2_FIPS_ 5102	26962	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_StatePlane_Hawaii_2_FIPS_ 5102_Feet	102662	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
NAD_1983_StatePlane_Hawaii_3_FIPS_ 5103	26963	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_StatePlane_Hawaii_3_FIPS_ 5103_Feet	3759	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
NAD_1983_StatePlane_Hawaii_4_FIPS_ 5104	26964	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_StatePlane_Hawaii_4_FIPS_ 5104_Feet	102664	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
NAD_1983_StatePlane_Hawaii_5_FIPS_ 5105	26965	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_StatePlane_Hawaii_5_FIPS_ 5105_Feet	102665	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
NAD_1983_StatePlane_Idaho_Central_ FIPS_1102	26969	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_StatePlane_Idaho_Central_ FIPS_1102_Feet	2242	USA - Idaho - SPCS - C	41.99	-115.3	45.7	-112.68
NAD_1983_StatePlane_Idaho_East_FIPS_ 1101	26968	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_StatePlane_Idaho_East_FIPS_ 1101_Feet	2241	USA - Idaho - SPCS - E	41.99	-113.24	44.75	-111.04
NAD_1983_StatePlane_Idaho_West_FIPS _1103	26970	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_StatePlane_Idaho_West_FIPS _1103_Feet	2243	USA - Idaho - SPCS - W	41.99	-117.24	49.01	-114.32
NAD_1983_StatePlane_Illinois_East_FIPS _1201	26971	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_StatePlane_Illinois_East_FIPS _1201_Feet	3435	USA - Illinois - SPCS - E	37.06	-89.28	42.5	-87.02
NAD_1983_StatePlane_Illinois_West_FIPS _1202	26972	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_StatePlane_Illinois_West_FIPS _1202_Feet	3436	USA - Illinois - SPCS - W	36.98	-91.52	42.51	-88.93
NAD_1983_StatePlane_Indiana_East_FIPS _1301	26973	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_StatePlane_Indiana_East_FIPS _1301_Feet	2965	USA - Indiana - SPCS - E	37.95	-86.59	41.77	-84.78
NAD_1983_StatePlane_Indiana_West_ FIPS_1302	26974	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_StatePlane_Indiana_West_ FIPS_1302_Feet	2966	USA - Indiana - SPCS - W	37.77	-88.06	41.77	-86.24
NAD_1983_StatePlane_Iowa_North_FIPS _1401	26975	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_StatePlane_Iowa_North_FIPS _1401_Feet	3417	USA - Iowa - SPCS - N	41.85	-96.65	43.51	-90.15
NAD_1983_StatePlane_Iowa_South_FIPS _1402	26976	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_StatePlane_Iowa_South_FIPS _1402_Feet	3418	USA - Iowa - SPCS - S	40.37	-96.14	42.04	-90.14
NAD_1983_StatePlane_Kansas_North_ FIPS_1501	26977	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_StatePlane_Kansas_North_ FIPS_1501_Feet	3419	USA - Kansas - SPCS - N	38.52	-102.06	40.01	-94.58
NAD_1983_StatePlane_Kansas_South_ FIPS_1502	26978	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_StatePlane_Kansas_South_ FIPS_1502_Feet	3420	USA - Kansas - SPCS - S	36.99	-102.05	38.88	-94.6
NAD_1983_StatePlane_Kentucky_FIPS_ 1600	3088	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_StatePlane_Kentucky_FIPS_ 1600_Feet	3089	USA - Kentucky	36.49	-89.57	39.15	-81.95
NAD_1983_StatePlane_Kentucky_North_ FIPS_1601	2205	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_StatePlane_Kentucky_North_ FIPS_1601_Feet	2246	USA - Kentucky - SPCS - N	37.71	-85.96	39.15	-82.47
NAD_1983_StatePlane_Kentucky_South_ FIPS_1602	26980	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_StatePlane_Kentucky_South_ FIPS_1602_Feet	2247	USA - Kentucky - SPCS - S	36.49	-89.57	38.17	-81.95
NAD_1983_StatePlane_Louisiana_North_ FIPS_1701	26981	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_StatePlane_Louisiana_North_ FIPS_1701_Feet	3451	USA - Louisiana - SPCS - N	30.85	-94.05	33.03	-90.86
NAD_1983_StatePlane_Louisiana_ Offshore_FIPS_1703	32199	USA - Louisiana	28.85	-94.05	33.03	-88.75
NAD_1983_StatePlane_Louisiana_ Offshore_FIPS_1703_Feet	3453	USA - Louisiana	28.85	-94.05	33.03	-88.75
NAD_1983_StatePlane_Louisiana_South_ FIPS_1702	26982	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_StatePlane_Louisiana_South_ FIPS_1702_Feet	3452	USA - Louisiana - SPCS83 - S	28.85	-93.94	31.07	-88.75
NAD_1983_StatePlane_Maine_East_FIPS _1801	26983	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_StatePlane_Maine_East_FIPS _1801_Feet	26847	USA - Maine - SPCS - E	43.88	-70.03	47.47	-66.91
NAD_1983_StatePlane_Maine_West_FIPS _1802	26984	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_StatePlane_Maine_West_FIPS _1802_Feet	26848	USA - Maine - SPCS - W	43.04	-71.09	46.58	-69.26
NAD_1983_StatePlane_Maryland_FIPS_ 1900	26985	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_StatePlane_Maryland_FIPS_ 1900_Feet	2248	USA - Maryland	37.97	-79.49	39.73	-74.97
NAD_1983_StatePlane_Massachusetts_ Island_FIPS_2002	26987	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_StatePlane_Massachusetts_ Island_FIPS_2002_Feet	2250	USA - Massachusetts - SPCS - islands	41.19	-70.91	41.51	-69.89
NAD_1983_StatePlane_Massachusetts_ Mainland_FIPS_2001	26986	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_StatePlane_Massachusetts_ Mainland_FIPS_2001_Feet	2249	USA - Massachusetts - SPCS - mainland	41.46	-73.5	42.89	-69.86
NAD_1983_StatePlane_Michigan_Central _FIPS_2112	26989	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_StatePlane_Michigan_Central _FIPS_2112_Feet	102689	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_StatePlane_Michigan_Central _FIPS_2112_Feet_Intl	2252	USA - Michigan - SPCS - C	43.8	-87.06	45.92	-82.27
NAD_1983_StatePlane_Michigan_North_ FIPS_2111	26988	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_StatePlane_Michigan_North_ FIPS_2111_Feet	102688	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_StatePlane_Michigan_North_ FIPS_2111_Feet_Intl	2251	USA - Michigan - SPCS - N	45.08	-90.42	48.32	-83.44
NAD_1983_StatePlane_Michigan_South_ FIPS_2113	26990	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_StatePlane_Michigan_South_ FIPS_2113_Feet	102690	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_StatePlane_Michigan_South_ FIPS_2113_Feet_Intl	2253	USA - Michigan - SPCS - S	41.69	-87.2	44.22	-82.13
NAD_1983_StatePlane_Minnesota_ Central_FIPS_2202	26992	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_StatePlane_Minnesota_ Central_FIPS_2202_Feet	26850	USA - Minnesota - SPCS - C	45.28	-96.86	47.48	-92.29
NAD_1983_StatePlane_Minnesota_North _FIPS_2201	26991	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_StatePlane_Minnesota_North _FIPS_2201_Feet	26849	USA - Minnesota - SPCS - N	46.64	-97.22	49.38	-89.49
NAD_1983_StatePlane_Minnesota_South _FIPS_2203	26993	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_StatePlane_Minnesota_South _FIPS_2203_Feet	26851	USA - Minnesota - SPCS - S	43.49	-96.85	45.59	-91.21
NAD_1983_StatePlane_Mississippi_East_ FIPS_2301	26994	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_StatePlane_Mississippi_East_ FIPS_2301_Feet	2254	USA - Mississippi - SPCS - E	30.01	-89.97	35.01	-88.09
NAD_1983_StatePlane_Mississippi_West _FIPS_2302	26995	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_StatePlane_Mississippi_West _FIPS_2302_Feet	2255	USA - Mississippi - SPCS - W	31	-91.65	35.01	-89.37
NAD_1983_StatePlane_Missouri_Central _FIPS_2402	26997	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_StatePlane_Missouri_Central _FIPS_2402_Feet	102697	USA - Missouri - SPCS - C	36.48	-93.79	40.61	-91.41
NAD_1983_StatePlane_Missouri_East_ FIPS_2401	26996	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_StatePlane_Missouri_East_ FIPS_2401_Feet	102696	USA - Missouri - SPCS - E	35.98	-91.97	40.61	-89.1
NAD_1983_StatePlane_Missouri_West_ FIPS_2403	26998	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_StatePlane_Missouri_West_ FIPS_2403_Feet	102698	USA - Missouri - SPCS - W	36.48	-95.77	40.59	-93.48
NAD_1983_StatePlane_Montana_FIPS_ 2500	32100	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_StatePlane_Montana_FIPS_ 2500_Feet	102700	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_StatePlane_Montana_FIPS_ 2500_Feet_Intl	2256	USA - Montana	44.35	-116.07	49.01	-104.04
NAD_1983_StatePlane_Nebraska_FIPS_ 2600	32104	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_StatePlane_Nebraska_FIPS_ 2600_Feet	26852	USA - Nebraska	39.99	-104.06	43.01	-95.3
NAD_1983_StatePlane_Nevada_Central_ FIPS_2702	32108	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_StatePlane_Nevada_Central_ FIPS_2702_Feet	3422	USA - Nevada - SPCS - C	36	-118.19	41	-114.99
NAD_1983_StatePlane_Nevada_East_ FIPS_2701	32107	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_StatePlane_Nevada_East_ FIPS_2701_Feet	3421	USA - Nevada - SPCS - E	34.99	-117.01	42	-114.03
NAD_1983_StatePlane_Nevada_West_ FIPS_2703	32109	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_StatePlane_Nevada_West_ FIPS_2703_Feet	3423	USA - Nevada - SPCS - W	36.95	-120	42	-116.99
NAD_1983_StatePlane_New_Hampshire_ FIPS_2800	32110	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_StatePlane_New_Hampshire_ FIPS_2800_Feet	3437	USA - New Hampshire	42.69	-72.56	45.31	-70.63
NAD_1983_StatePlane_New_Jersey_FIPS _2900	32111	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_StatePlane_New_Jersey_FIPS _2900_Feet	3424	USA - New Jersey	38.87	-75.6	41.36	-73.88
NAD_1983_StatePlane_New_Mexico_ Central_FIPS_3002	32113	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_StatePlane_New_Mexico_ Central_FIPS_3002_Feet	2258	USA - New Mexico - SPCS83 - C	31.78	-107.73	37	-104.84
NAD_1983_StatePlane_New_Mexico_ East_FIPS_3001	32112	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_StatePlane_New_Mexico_ East_FIPS_3001_Feet	2257	USA - New Mexico - SPCS - E	32	-105.72	37	-102.99
NAD_1983_StatePlane_New_Mexico_ West_FIPS_3003	32114	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_StatePlane_New_Mexico_ West_FIPS_3003_Feet	2259	USA - New Mexico - SPCS83 - W	31.33	-109.06	37	-106.32
NAD_1983_StatePlane_New_York_ Central_FIPS_3102	32116	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_StatePlane_New_York_ Central_FIPS_3102_Feet	2261	USA - New York - SPCS - C	41.99	-77.75	44.41	-75.04
NAD_1983_StatePlane_New_York_East_ FIPS_3101	32115	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_StatePlane_New_York_East_ FIPS_3101_Feet	2260	USA - New York - SPCS - E	40.88	-75.87	45.02	-73.23
NAD_1983_StatePlane_New_York_Long_ Island_FIPS_3104	32118	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_StatePlane_New_York_Long_ Island_FIPS_3104_Feet	2263	USA - New York - SPCS - Long Island	40.47	-74.26	41.3	-71.8
NAD_1983_StatePlane_New_York_West_ FIPS_3103	32117	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_StatePlane_New_York_West_ FIPS_3103_Feet	2262	USA - New York - SPCS - W	41.99	-79.77	43.64	-77.36
NAD_1983_StatePlane_North_Carolina_ FIPS_3200	32119	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_StatePlane_North_Carolina_ FIPS_3200_Feet	2264	USA - North Carolina	33.83	-84.33	36.59	-75.38
NAD_1983_StatePlane_North_Dakota_ North_FIPS_3301	32120	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_StatePlane_North_Dakota_ North_FIPS_3301_Feet	102720	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_StatePlane_North_Dakota_ North_FIPS_3301_Feet_Intl	2265	USA - North Dakota - SPCS - N	47.15	-104.07	49.01	-96.83
NAD_1983_StatePlane_North_Dakota_ South_FIPS_3302	32121	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_StatePlane_North_Dakota_ South_FIPS_3302_Feet	102721	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_StatePlane_North_Dakota_ South_FIPS_3302_Feet_Intl	2266	USA - North Dakota - SPCS - S	45.93	-104.05	47.83	-96.55
NAD_1983_StatePlane_Ohio_North_FIPS _3401	32122	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_StatePlane_Ohio_North_FIPS _3401_Feet	3734	USA - Ohio - SPCS - N	40.1	-84.81	42.33	-80.51
NAD_1983_StatePlane_Ohio_South_FIPS _3402	32123	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_StatePlane_Ohio_South_FIPS _3402_Feet	3735	USA - Ohio - SPCS - S	38.4	-84.83	40.36	-80.7
NAD_1983_StatePlane_Oklahoma_North _FIPS_3501	32124	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_StatePlane_Oklahoma_North _FIPS_3501_Feet	2267	USA - Oklahoma - SPCS - N	35.27	-103	37.01	-94.42
NAD_1983_StatePlane_Oklahoma_South _FIPS_3502	32125	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_StatePlane_Oklahoma_South _FIPS_3502_Feet	2268	USA - Oklahoma - SPCS - S	33.62	-100	35.57	-94.42
NAD_1983_StatePlane_Oregon_North_ FIPS_3601	32126	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_StatePlane_Oregon_North_ FIPS_3601_Feet	102726	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_StatePlane_Oregon_North_ FIPS_3601_Feet_Intl	2269	USA - Oregon - SPCS - N	43.95	-124.17	46.26	-116.47
NAD_1983_StatePlane_Oregon_South_ FIPS_3602	32127	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_StatePlane_Oregon_South_ FIPS_3602_Feet	102727	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_StatePlane_Oregon_South_ FIPS_3602_Feet_Intl	2270	USA - Oregon - SPCS - S	41.98	-124.6	44.56	-116.9
NAD_1983_StatePlane_Pennsylvania_ North_FIPS_3701	32128	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_StatePlane_Pennsylvania_ North_FIPS_3701_Feet	2271	USA - Pennsylvania - SPCS - N	40.6	-80.53	42.53	-74.7
NAD_1983_StatePlane_Pennsylvania_ South_FIPS_3702	32129	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_StatePlane_Pennsylvania_ South_FIPS_3702_Feet	2272	USA - Pennsylvania - SPCS - S	39.71	-80.53	41.18	-74.72
NAD_1983_StatePlane_Puerto_Rico_ Virgin_Islands_FIPS_5200	32161	Caribbean - Puerto Rico and US Virgin Islands	14.92	-68.49	21.86	-63.88
NAD_1983_StatePlane_Puerto_Rico_ Virgin_Islands_FIPS_5200_Feet	102761	Caribbean - Puerto Rico and US Virgin Islands	14.92	-68.49	21.86	-63.88
NAD_1983_StatePlane_Rhode_Island_ FIPS_3800	32130	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_StatePlane_Rhode_Island_ FIPS_3800_Feet	3438	USA - Rhode Island	41.13	-71.85	42.02	-71.08
NAD_1983_StatePlane_South_Carolina_ FIPS_3900	32133	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_StatePlane_South_Carolina_ FIPS_3900_Feet	102733	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_StatePlane_South_Carolina_ FIPS_3900_Feet_Intl	2273	USA - South Carolina	32.05	-83.36	35.21	-78.52
NAD_1983_StatePlane_South_Dakota_ North_FIPS_4001	32134	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_StatePlane_South_Dakota_ North_FIPS_4001_Feet	4457	USA - South Dakota - SPCS - N	44.14	-104.07	45.95	-96.45
NAD_1983_StatePlane_South_Dakota_ South_FIPS_4002	32135	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_StatePlane_South_Dakota_ South_FIPS_4002_Feet	3455	USA - South Dakota - SPCS - S	42.48	-104.06	44.79	-96.43
NAD_1983_StatePlane_Tennessee_FIPS_ 4100	32136	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_StatePlane_Tennessee_FIPS_ 4100_Feet	2274	USA - Tennessee	34.98	-90.31	36.68	-81.65
NAD_1983_StatePlane_Texas_Central_ FIPS_4203	32139	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_StatePlane_Texas_Central_ FIPS_4203_Feet	2277	USA - Texas - SPCS - C	29.78	-106.66	32.27	-93.5
NAD_1983_StatePlane_Texas_North_ Central_FIPS_4202	32138	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_StatePlane_Texas_North_ Central_FIPS_4202_Feet	2276	USA - Texas - SPCS - NC	31.72	-103.07	34.58	-94
NAD_1983_StatePlane_Texas_North_FIPS _4201	32137	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_StatePlane_Texas_North_FIPS _4201_Feet	2275	USA - Texas - SPCS - N	34.3	-103.03	36.5	-99.99
NAD_1983_StatePlane_Texas_South_ Central_FIPS_4204	32140	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_StatePlane_Texas_South_ Central_FIPS_4204_Feet	2278	USA - Texas - SPCS83 - SC	27.78	-105	30.67	-93.76
NAD_1983_StatePlane_Texas_South_FIPS _4205	32141	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_StatePlane_Texas_South_FIPS _4205_Feet	2279	USA - Texas - SPCS83 - S	25.83	-100.2	28.21	-96.85
NAD_1983_StatePlane_Utah_Central_ FIPS_4302	32143	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_StatePlane_Utah_Central_ FIPS_4302_Feet	3566	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_StatePlane_Utah_Central_ FIPS_4302_Feet_Intl	2281	USA - Utah - SPCS - C	38.49	-114.05	41.08	-109.04
NAD_1983_StatePlane_Utah_North_FIPS _4301	32142	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_StatePlane_Utah_North_FIPS _4301_Feet	3560	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_StatePlane_Utah_North_FIPS _4301_Feet_Intl	2280	USA - Utah - SPCS - N	40.55	-114.04	42.01	-109.04
NAD_1983_StatePlane_Utah_South_FIPS _4303	32144	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_StatePlane_Utah_South_FIPS _4303_Feet	3567	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_StatePlane_Utah_South_FIPS _4303_Feet_Intl	2282	USA - Utah - SPCS - S	36.99	-114.05	38.58	-109.04
NAD_1983_StatePlane_Vermont_FIPS_ 4400	32145	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_StatePlane_Vermont_FIPS_ 4400_Feet	5646	USA - Vermont	42.72	-73.44	45.03	-71.5
NAD_1983_StatePlane_Virginia_North_ FIPS_4501	32146	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_StatePlane_Virginia_North_ FIPS_4501_Feet	2283	USA - Virginia - SPCS - N	37.77	-80.06	39.46	-76.51
NAD_1983_StatePlane_Virginia_South_ FIPS_4502	32147	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_StatePlane_Virginia_South_ FIPS_4502_Feet	2284	USA - Virginia - SPCS - S	36.54	-83.68	38.28	-75.31
NAD_1983_StatePlane_Washington_ North_FIPS_4601	32148	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_StatePlane_Washington_ North_FIPS_4601_Feet	2285	USA - Washington - SPCS83 - N	47.08	-124.79	49.05	-117.02
NAD_1983_StatePlane_Washington_ South_FIPS_4602	32149	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_StatePlane_Washington_ South_FIPS_4602_Feet	2286	USA - Washington - SPCS83 - S	45.54	-124.4	47.61	-116.91
NAD_1983_StatePlane_West_Virginia_ North_FIPS_4701	32150	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_StatePlane_West_Virginia_ North_FIPS_4701_Feet	26853	USA - West Virginia - SPCS - N	38.76	-81.76	40.64	-77.72
NAD_1983_StatePlane_West_Virginia_ South_FIPS_4702	32151	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_StatePlane_West_Virginia_ South_FIPS_4702_Feet	26854	USA - West Virginia - SPCS - S	37.2	-82.65	39.17	-79.05
NAD_1983_StatePlane_Wisconsin_ Central_FIPS_4802	32153	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_StatePlane_Wisconsin_ Central_FIPS_4802_Feet	2288	USA - Wisconsin - SPCS - C	43.98	-92.89	45.8	-86.25
NAD_1983_StatePlane_Wisconsin_North _FIPS_4801	32152	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_StatePlane_Wisconsin_North _FIPS_4801_Feet	2287	USA - Wisconsin - SPCS - N	45.37	-92.89	47.31	-88.05
NAD_1983_StatePlane_Wisconsin_South _FIPS_4803	32154	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_StatePlane_Wisconsin_South _FIPS_4803_Feet	2289	USA - Wisconsin - SPCS - S	42.48	-91.43	44.33	-86.95
NAD_1983_StatePlane_Wyoming_East_ Central_FIPS_4902	32156	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_StatePlane_Wyoming_East_ Central_FIPS_4902_Feet	3737	USA - Wyoming - SPCS - EC	40.99	-108.63	45.01	-106
NAD_1983_StatePlane_Wyoming_East_ FIPS_4901	32155	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_StatePlane_Wyoming_East_ FIPS_4901_Feet	3736	USA - Wyoming - SPCS - E	40.99	-106.33	45.01	-104.05
NAD_1983_StatePlane_Wyoming_West_ Central_FIPS_4903	32157	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_StatePlane_Wyoming_West_ Central_FIPS_4903_Feet	3738	USA - Wyoming - SPCS - WC	40.99	-111.06	45.01	-107.5
NAD_1983_StatePlane_Wyoming_West_ FIPS_4904	32158	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_StatePlane_Wyoming_West_ FIPS_4904_Feet	3739	USA - Wyoming - SPCS - W	40.99	-111.06	44.67	-109.04
NAD_1983_Statistics_Canada_Lambert	3347	Canada	38.21	-141.01	86.46	-40.73
NAD_1983_Teranet_Ontario_Lambert	5320	Canada - Ontario	41.67	-95.16	56.9	-74.35
NAD_1983_Texas_Centric_Mapping_ System_Albers	3083	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_Texas_Centric_Mapping_ System_Lambert	3082	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_Texas_Statewide_Mapping_ System	3081	USA - Texas	25.83	-106.66	36.5	-93.5
NAD_1983_USFS_R6_Albers	102218	USA - Oregon and Washington	41.98	-124.79	49.05	-116.47
NAD_1983_USFS_R9_Albers	102042	USA - USFS - Eastern Region	35.9	-97.3	49.5	-66.8
NAD_1983_UTM_Zone_10N	26910	North America - 126°W to 120°W and NAD83 by country	30.54	-126	81.8	-119.99
NAD_1983_UTM_Zone_11N	26911	North America - 120°W to 114°W and NAD83 by country	30.88	-120	83.5	-114
NAD_1983_UTM_Zone_12N	26912	North America - 114°W to 108°W and NAD83 by country	31.33	-114	84	-108
NAD_1983_UTM_Zone_13N	26913	North America - 108°W to 102°W and NAD83 by country	28.98	-108	84	-102
NAD_1983_UTM_Zone_14N	26914	North America - 102°W to 96°W and NAD83 by country	25.83	-102	84	-96
NAD_1983_UTM_Zone_15N	26915	North America - 96°W to 90°W and NAD83 by country	25.61	-96	84	-90
NAD_1983_UTM_Zone_16N	26916	North America - 90°W to 84°W and NAD83 by country	23.97	-90	84	-84
NAD_1983_UTM_Zone_17N	26917	North America - 84°W to 78°W and NAD83 by country	23.81	-84	84	-78
NAD_1983_UTM_Zone_18N	26918	North America - 78°W to 72°W and NAD83 by country	28.28	-78	84	-72
NAD_1983_UTM_Zone_19N	26919	North America - 72°W to 66°W and NAD83 by country	14.92	-72	84	-66
NAD_1983_UTM_Zone_1N	26901	USA - 180°W to 174°W - AK, OCS	47.88	-180	63.21	-173.99
NAD_1983_UTM_Zone_20N	26920	North America - 66°W to 60°W and NAD83 by country	15.63	-66	84	-60
NAD_1983_UTM_Zone_21N	26921	Canada - 60°W to 54°W	38.56	-60	84	-54
NAD_1983_UTM_Zone_22N	26922	Canada - 54°W to 48°W	39.5	-54	57.65	-48
NAD_1983_UTM_Zone_23N	26923	Canada - 48°W to 42°W	39.85	-48	54.47	-47.74
NAD_1983_UTM_Zone_24N	9712	Canada - east of 42°W	45.53	-42	49.53	-40.73
NAD_1983_UTM_Zone_2N	26902	USA - 174°W to 168°W - AK, OCS	48.66	-174	73.05	-167.99
NAD_1983_UTM_Zone_3N	26903	USA - 168°W to 162°W - AK, OCS	49.52	-168	74.29	-161.99
NAD_1983_UTM_Zone_4N	26904	USA - 162°W to 156°W - AK, HI	15.57	-162	74.71	-155.99
NAD_1983_UTM_Zone_58N	102213	World - N hemisphere - 168°E to 174°E - by country	0	168	84	174
NAD_1983_UTM_Zone_59N	3372	USA - west of 174°E - AK, OCS	49.01	167.65	56.28	174.01
NAD_1983_UTM_Zone_5N	26905	USA - 156°W to 150°W - AK, HI	15.56	-156	74.71	-149.99
NAD_1983_UTM_Zone_60N	3373	USA - 174°E to 180°E - AK, OCS	47.92	174	56.67	180
NAD_1983_UTM_Zone_6N	26906	USA - 150°W to 144°W - AK, OCS	54.05	-150	74.13	-143.99
NAD_1983_UTM_Zone_7N	26907	North America - 144°W to 138°W and NAD83 by country	52.05	-144	73.59	-137.99
NAD_1983_UTM_Zone_8N	26908	North America - 138°W to 132°W and NAD83 by country	48.06	-138	79.42	-132
NAD_1983_UTM_Zone_9N	26909	North America - 132°W to 126°W and NAD83 by country	35.38	-132	80.93	-126
NAD_1983_Virginia_Lambert	3968	USA - Virginia	36.54	-83.68	39.46	-75.31
NAD_1983_Wisconsin_TM	3070	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_Wisconsin_TM_US_Ft	102219	USA - Wisconsin	42.48	-92.89	47.31	-86.25
NAD_1983_WyLAM	102212	USA - Wyoming	40.99	-111.06	45.01	-104.05
NAD_1983_Yukon_Albers	3578	Canada - Yukon	59.99	-141.01	69.7	-123.91

Projected Coordinate Systems Part Three

Name	WKID	Area of Use	Minimum Latitude	Minimum Longitude	Maximum Latitude	Maximum Longitude
Nahrwan_1934_Iraq_Zone	3394	Asia - Middle East -SE Iraq and SW Iran	29.06	44.3	33.5	51.06
Nahrwan_1934_UTM_zone_37N	7005	Iraq - west of 42°E	31.14	38.79	36.75	42
Nahrwan_1934_UTM_zone_38N	7006	Iraq - 42°E to 48°E	29.06	42	37.39	48
Nahrwan_1934_UTM_zone_39N	7007	Iraq - east of 48°E	29.6	48	31	48.75
Nahrwan_1967_UTM_Zone_37N	27037	Iraq - west of 42°E	31.14	38.79	36.75	42
Nahrwan_1967_UTM_Zone_38N	27038	Asia - Middle East - Iraq and Kuwait 42°E to 48°E	28.53	42	37.39	48
Nahrwan_1967_UTM_Zone_39N	27039	Asia - Middle East - Qatar offshore and UAE west of 54°E	22.76	50.55	27.05	54.01
Nahrwan_1967_UTM_Zone_40N	27040	UAE - east of 54°E	22.63	54	26.27	57.13
Nakhl-e_Ghanem_UTM_Zone_39N	3307	Iran - Kangan district	27.3	51.8	28.2	53.01
Naparima_1955_UTM_Zone_20N	2067	Trinidad and Tobago - Trinidad - onshore	9.99	-61.98	10.9	-60.85
Naparima_1972_UTM_Zone_20N	27120	Trinidad and Tobago - Tobago - onshore	11.08	-60.9	11.41	-60.44
NEA74_Noumea_Lambert	3165	New Caledonia - Grande Terre - Noumea	-22.37	166.35	-22.19	166.54
NEA74_Noumea_Lambert_2	3166	New Caledonia - Grande Terre - Noumea	-22.37	166.35	-22.19	166.54
NEA74_Noumea_UTM_58S	2998	New Caledonia - Grande Terre - Noumea	-22.37	166.35	-22.19	166.54
Nepal_Nagarkot_TM	102306	Nepal	26.34	80.06	30.43	88.21
New_Beijing_3_Degree_Gauss_Kruger_ CM_102E	4791	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_105E	4792	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
New_Beijing_3_Degree_Gauss_Kruger_ CM_108E	4793	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
New_Beijing_3_Degree_Gauss_Kruger_ CM_111E	4794	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_114E	4795	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_117E	4796	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_120E	4797	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_123E	4798	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_126E	4799	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_129E	4800	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_132E	102569	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_135E	4822	China - east of 133.5°E	45.85	133.5	48.4	134.77
New_Beijing_3_Degree_Gauss_Kruger_ CM_75E	4782	China - west of 76.5°E	35.81	73.62	40.65	76.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_78E	4783	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_81E	4784	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
New_Beijing_3_Degree_Gauss_Kruger_ CM_84E	4785	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_87E	4786	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_90E	4787	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
New_Beijing_3_Degree_Gauss_Kruger_ CM_93E	4788	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
New_Beijing_3_Degree_Gauss_Kruger_ CM_96E	4789	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
New_Beijing_3_Degree_Gauss_Kruger_ CM_99E	4790	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_25	4652	China - west of 76.5°E	35.81	73.62	40.65	76.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_26	4653	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_27	4654	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
New_Beijing_3_Degree_Gauss_Kruger_ Zone_28	4655	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_29	4656	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_30	4766	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
New_Beijing_3_Degree_Gauss_Kruger_ Zone_31	4767	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_32	4768	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
New_Beijing_3_Degree_Gauss_Kruger_ Zone_33	4769	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_34	4770	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_35	4771	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
New_Beijing_3_Degree_Gauss_Kruger_ Zone_36	4772	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
New_Beijing_3_Degree_Gauss_Kruger_ Zone_37	4773	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_38	4774	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_39	4775	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_40	4776	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_41	4777	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_42	4778	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_43	4779	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_44	4780	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
New_Beijing_3_Degree_Gauss_Kruger_ Zone_45	4781	China - east of 133.5°E	45.85	133.5	48.4	134.77
New_Beijing_Gauss_Kruger_CM_105E	4584	China - 102°E to 108°E onshore	21.53	102	42.47	108
New_Beijing_Gauss_Kruger_CM_111E	4585	China - 108°E to 114°E onshore	18.11	108	45.11	114
New_Beijing_Gauss_Kruger_CM_117E	4586	China - 114°E to 120°E onshore	22.14	114	51.52	120
New_Beijing_Gauss_Kruger_CM_123E	4587	China - 120°E to 126°E onshore	26.34	120	53.56	126
New_Beijing_Gauss_Kruger_CM_129E	4588	China - 126°E to 132°E onshore	40.89	126	52.79	132
New_Beijing_Gauss_Kruger_CM_135E	4589	China - east of 132°E	45.02	132	48.4	134.77
New_Beijing_Gauss_Kruger_CM_75E	4579	China - west of 78°E	35.42	73.62	41.07	78.01
New_Beijing_Gauss_Kruger_CM_81E	4580	China - 78°E to 84°E	29.16	77.98	47.23	84
New_Beijing_Gauss_Kruger_CM_87E	4581	China - 84°E to 90°E	27.32	84	49.18	90
New_Beijing_Gauss_Kruger_CM_93E	4582	China - 90°E to 96°E	27.71	90	47.9	96.01
New_Beijing_Gauss_Kruger_CM_99E	4583	China - 96°E to 102°E	21.13	96	43.18	102.01
New_Beijing_Gauss_Kruger_Zone_13	4568	China - west of 78°E	35.43	73.62	41.07	78.01
New_Beijing_Gauss_Kruger_Zone_14	4569	China - 78°E to 84°E	29.16	77.98	47.23	84
New_Beijing_Gauss_Kruger_Zone_15	4570	China - 84°E to 90°E	27.32	84	49.18	90
New_Beijing_Gauss_Kruger_Zone_16	4571	China - 90°E to 96°E	27.71	90	47.9	96.01
New_Beijing_Gauss_Kruger_Zone_17	4572	China - 96°E to 102°E	21.13	96	43.18	102.01
New_Beijing_Gauss_Kruger_Zone_18	4573	China - 102°E to 108°E onshore	21.53	102	42.47	108
New_Beijing_Gauss_Kruger_Zone_19	4574	China - 108°E to 114°E onshore	18.11	108	45.11	114
New_Beijing_Gauss_Kruger_Zone_20	4575	China - 114°E to 120°E onshore	22.14	114	51.52	120
New_Beijing_Gauss_Kruger_Zone_21	4576	China - 120°E to 126°E onshore	26.34	120	53.56	126
New_Beijing_Gauss_Kruger_Zone_22	4577	China - 126°E to 132°E onshore	40.89	126	52.79	132
New_Beijing_Gauss_Kruger_Zone_23	4578	China - east of 132°E	45.02	132	48.4	134.77
New_Zealand_North_Island	27291	New Zealand - North Island	-41.67	171.99	-34.1	178.63
New_Zealand_South_Island	27292	New Zealand - South and Stewart Islands	-47.33	166.37	-40.44	174.46
NGN_UTM_Zone_38N	31838	Kuwait - west of 48°E onshore	28.53	46.54	30.09	48
NGN_UTM_Zone_39N	31839	Kuwait - east of 48°E onshore	28.54	48	30.04	48.48
NGO_1948_Baerum_Kommune	102136	Norway - Baerum Kommune	59.825	10.337	60.037	10.672
NGO_1948_Bergenhalvoen	102137	Norway - Bergenhalvoen Kommune	60.165	5.137	60.544	5.699
NGO_1948_Norway_Zone_1	102101	Norway - zone I	57.93	4.68	63.06	7.23
NGO_1948_Norway_Zone_2	102102	Norway - zone II	57.95	7.22	63.87	9.56
NGO_1948_Norway_Zone_3	102103	Norway - zone III	58.84	9.55	65.76	11.98
NGO_1948_Norway_Zone_4	102104	Norway - zone IV	59.88	11.97	69.06	15.06
NGO_1948_Norway_Zone_5	102105	Norway - zone V	66.15	15.05	70.19	18.89
NGO_1948_Norway_Zone_6	102106	Norway - zone VI	68.33	18.88	70.81	22.89
NGO_1948_Norway_Zone_7	102107	Norway - zone VII	68.58	22.88	71.21	26.98
NGO_1948_Norway_Zone_8	102108	Norway - zone VIII	69.02	26.97	71.17	31.22
NGO_1948_Oslo_Baerum_Kommune	102450	Norway - Baerum Kommune	59.825	10.337	60.037	10.672
NGO_1948_Oslo_Bergenhalvoen	102451	Norway - Bergenhalvoen Kommune	60.165	5.137	60.544	5.699
NGO_1948_Oslo_Kommune	102138	Norway - Oslo Kommune	59.81	10.48	60.14	10.97
NGO_1948_Oslo_Norway_Zone_1	27391	Norway - zone I	57.93	4.68	63.06	7.23
NGO_1948_Oslo_Norway_Zone_2	27392	Norway - zone II	57.95	7.22	63.87	9.56
NGO_1948_Oslo_Norway_Zone_3	27393	Norway - zone III	58.84	9.55	65.76	11.98
NGO_1948_Oslo_Norway_Zone_4	27394	Norway - zone IV	59.88	11.97	69.06	15.06
NGO_1948_Oslo_Norway_Zone_5	27395	Norway - zone V	66.15	15.05	70.19	18.89
NGO_1948_Oslo_Norway_Zone_6	27396	Norway - zone VI	68.33	18.88	70.81	22.89
NGO_1948_Oslo_Norway_Zone_7	27397	Norway - zone VII	68.58	22.88	71.21	26.98
NGO_1948_Oslo_Norway_Zone_8	27398	Norway - zone VIII	69.02	26.97	71.17	31.22
NGO_1948_Oslo_Oslo_Kommune	102452	Norway - Oslo Kommune	59.81	10.48	60.14	10.97
NGO_1948_UTM_Zone_32N	102132	World - N hemisphere - 6°E to 12°E - by country	0	6	84	12
NGO_1948_UTM_Zone_33N	102133	World - N hemisphere - 12°E to 18°E - by country	0	12	84	18
NGO_1948_UTM_Zone_34N	102134	World - N hemisphere - 18°E to 24°E - by country	0	18	84	24
NGO_1948_UTM_Zone_35N	102135	World - N hemisphere - 24°E to 30°E - by country	0	24	84	30
Nigeria_East_Belt	26393	Nigeria - east of 10.5°E	6.43	10.49	13.72	14.65
Nigeria_Mid_Belt	26392	Nigeria - 6.5°E to 10.5°E	3.57	6.5	13.53	10.51
Nigeria_West_Belt	26391	Nigeria - west of 6.5°E	3.57	2.69	13.9	6.5
Nord_Algerie_Ancienne	30491	Algeria - north of 34°39'N	34.64	-2.22	37.14	8.64
Nord_Algerie_Ancienne_Degree	102491	Algeria	18.97	-8.67	38.8	11.99
Nord_de_Guerre	27500	France - Alsace	47.42	6.84	49.07	8.23
Nord_Maroc	26191	Morocco - north of 31.5°N	31.49	-9.85	35.97	-1.01
Nord_Maroc_Degree	102191	Morocco - north of 31.5°N	31.49	-9.85	35.97	-1.01
Nord_Sahara_1959_UTM_Zone_29N	30729	Algeria - west of 6°W	25.73	-8.67	29.85	-6
Nord_Sahara_1959_UTM_Zone_30N	30730	Algeria - 6°W to 0°W	21.82	-6	37.01	0
Nord_Sahara_1959_UTM_Zone_31N	30731	Algeria - 0°E to 6°E	18.97	0	38.77	6.01
Nord_Sahara_1959_UTM_Zone_32N	30732	Algeria - east of 6°E	19.6	6	38.8	11.99
Nord_Sahara_1959_Voirol_Unifie_Nord	30791	Algeria - north of 34°39'N	34.64	-2.22	37.14	8.64
Nord_Sahara_1959_Voirol_Unifie_Sud	30792	Algeria - 31°30'N to 34°39'N	31.49	-3.85	34.66	9.22
Nord_Tunisie	22391	Tunisia - north of 34°39'N	34.65	8.18	37.4	11.37
North_America_Albers_Equal_Area_ Conic	102008	North America - Canada and USA (CONUS, Alaska mainland)	23.81	-172.54	86.46	-47.74
North_America_Equidistant_Conic	102010	North America - Canada and USA (CONUS, Alaska mainland)	23.81	-172.54	86.46	-47.74
North_America_Lambert_Conformal_ Conic	102009	North America - Canada and USA (CONUS, Alaska mainland)	23.81	-172.54	86.46	-47.74
North_Pole_Azimuthal_Equidistant	102016	World - north of 0°N	0	-180	90	180
North_Pole_Gnomonic	102034	World - north of 0°N	0	-180	90	180
North_Pole_Lambert_Azimuthal_Equal_ Area	102017	World - north of 0°N	0	-180	90	180
North_Pole_Orthographic	102035	World - north of 0°N	0	-180	90	180
North_Pole_Stereographic	102018	World - north of 0°N	0	-180	90	180
NSIDC_EASE_Grid_Global	3410	World - 86°S to 86°N	-86	-180	86	180
NSIDC_EASE_Grid_North	3408	World - north of 0°N	0	-180	90	180
NSIDC_EASE_Grid_South	3409	World - south of 0°N	-90	-180	0	180
NSIDC_Sea_Ice_Polar_Stereographic_ North	3411	World - N hemisphere - north of 60°N	60	-180	90	180
NSIDC_Sea_Ice_Polar_Stereographic_ South	3412	World - S hemisphere - south of 60°S	-90	-180	-60	180
NTF_France_I_degrees	102581	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_France_II_degrees	102582	France - mainland 45.45°N to 48.15°N. Also all mainland.	42.33	-4.87	51.14	8.23
NTF_France_III_degrees	102583	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NTF_France_IV_degrees	102584	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Lambert_Zone_I	102585	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_Lambert_Zone_II	102586	France - mainland 45.45°N to 48.15°N. Also all mainland.	42.33	-4.87	51.14	8.23
NTF_Lambert_Zone_III	102587	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NTF_Lambert_Zone_IV	102588	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Paris_Centre_France	27592	France - mainland 45.45°N to 48.15°N	45.44	-4.8	48.15	7.63
NTF_Paris_Corse	27594	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Paris_France_I	27581	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_Paris_France_II	27582	France - mainland 45.45°N to 48.15°N. Also all mainland.	42.33	-4.87	51.14	8.23
NTF_Paris_France_III	27583	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NTF_Paris_France_IV	27584	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Paris_Lambert_Centre_France	27562	France - mainland 45.45°N to 48.15°N	45.44	-4.8	48.15	7.63
NTF_Paris_Lambert_Corse	27564	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Paris_Lambert_Nord_France	27561	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_Paris_Lambert_Sud_France	27563	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NTF_Paris_Lambert_Zone_I	27571	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_Paris_Lambert_Zone_II	27572	France - mainland 45.45°N to 48.15°N. Also all mainland.	42.33	-4.87	51.14	8.23
NTF_Paris_Lambert_Zone_III	27573	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NTF_Paris_Lambert_Zone_IV	27574	France - Corsica onshore	41.31	8.5	43.07	9.63
NTF_Paris_Nord_France	27591	France - mainland north of 48.15°N	48.14	-4.87	51.14	8.23
NTF_Paris_Sud_France	27593	France - mainland south of 45.45°N	42.33	-1.79	45.46	7.71
NZGD_1949_Amuri_Circuit	27219	New Zealand - South Island - Amuri mc	-42.95	171.88	-42.09	173.55
NZGD_1949_Bay_of_Plenty_Circuit	27206	New Zealand - North Island - Bay of Plenty mc	-39.13	175.75	-37.22	177.23
NZGD_1949_Bluff_Circuit	27232	New Zealand - South and Stewart Islands - Bluff mc	-47.33	167.29	-45.33	168.97
NZGD_1949_Buller_Circuit	27217	New Zealand - South Island - Buller mc	-42.19	171.27	-41.42	172.41
NZGD_1949_Collingwood_Circuit	27214	New Zealand - South Island - Collingwood mc	-41.22	172.16	-40.44	173.13
NZGD_1949_Gawler_Circuit	27225	New Zealand - South Island - Gawler mc	-44.25	170.68	-43.13	172.26
NZGD_1949_Grey_Circuit	27218	New Zealand - South Island - Grey mc	-42.74	171.15	-41.5	172.75
NZGD_1949_Hawkes_Bay_Circuit	27208	New Zealand - North Island - Hawkes Bay mc Napier vcrs	-40.57	175.8	-38.87	178.07
NZGD_1949_Hokitika_Circuit	27221	New Zealand - South Island - Hokitika mc	-43.23	170.39	-42.41	171.89
NZGD_1949_Jacksons_Bay_Circuit	27223	New Zealand - South Island - Jacksons Bay mc	-44.4	168.02	-43.67	170.01
NZGD_1949_Karamea_Circuit	27216	New Zealand - South Island - Karamea mc	-41.49	171.96	-40.75	172.7
NZGD_1949_Lindis_Peak_Circuit	27227	New Zealand - South Island - Lindis Peak mc	-45.4	168.62	-43.71	170.24
NZGD_1949_Marlborough_Circuit	27220	New Zealand - South Island - Marlborough mc	-42.65	172.95	-40.85	174.46
NZGD_1949_Mount_Eden_Circuit	27205	New Zealand - North Island - Mount Eden mc	-39.01	171.99	-34.1	176.12
NZGD_1949_Mount_Nicholas_Circuit	27228	New Zealand - South Island - Mount Nicholas mc	-45.58	167.72	-44.29	169.11
NZGD_1949_Mount_Pleasant_Circuit	27224	New Zealand - South Island - Mount Pleasant mc	-43.96	171.11	-42.69	173.38
NZGD_1949_Mount_York_Circuit	27229	New Zealand - South Island - Mount York mc	-46.33	166.37	-44.53	168.21
NZGD_1949_Nelson_Circuit	27215	New Zealand - South Island - Nelson mc	-42.18	172.4	-40.66	174.08
NZGD_1949_North_Taieri_Circuit	27231	New Zealand - South Island - North Taieri mc	-46.73	168.64	-45.23	170.87
NZGD_1949_Observation_Point_Circuit	27230	New Zealand - South Island - Observation Point mc	-45.82	169.77	-44.61	171.24
NZGD_1949_Okarito_Circuit	27222	New Zealand - South Island - Okarito mc	-43.85	169.21	-43	170.89
NZGD_1949_Poverty_Bay_Circuit	27207	New Zealand - North Island - Poverty Bay mc	-39.04	176.73	-37.49	178.63
NZGD_1949_Taranaki_Circuit	27209	New Zealand - North Island - Taranaki mc	-39.78	173.68	-38.4	175.44
NZGD_1949_Timaru_Circuit	27226	New Zealand - South Island - Timaru mc	-44.98	169.82	-43.35	171.55
NZGD_1949_Tuhirangi_Circuit	27210	New Zealand - North Island - Tuhirangi mc	-39.55	174.88	-38.87	176.33
NZGD_1949_UTM_Zone_58S	27258	New Zealand - nearshore west of 168°E	-47.65	165.87	-42.59	168
NZGD_1949_UTM_Zone_59S	27259	New Zealand - nearshore 168°E to 174°E	-47.64	168	-33.89	174
NZGD_1949_UTM_Zone_60S	27260	New Zealand - nearshore east of 174°E	-44.13	174	-34.24	179.27
NZGD_1949_Wairarapa_Circuit	27212	New Zealand - North Island - Wairarapa mc	-41.67	175.01	-40.29	176.55
NZGD_1949_Wanganui_Circuit	27211	New Zealand - North Island - Wanganui mc	-40.97	174.4	-39.46	176.27
NZGD_1949_Wellington_Circuit	27213	New Zealand - North Island - Wellington mc	-41.5	174.52	-40.91	175.36
NZGD_2000_Amuri_Circuit	2119	New Zealand - South Island - Amuri mc	-42.95	171.88	-42.09	173.55
NZGD_2000_Antipodes_Islands_TM_ 2000	3790	New Zealand - Antipodes and Bounty Islands	-49.92	178.4	-47.54	179.37
NZGD_2000_Auckland_Islands_TM_2000	3788	New Zealand - Snares and Auckland Islands	-51.13	165.55	-47.8	166.93
NZGD_2000_Bay_of_Plenty_Circuit	2106	New Zealand - North Island - Bay of Plenty mc	-39.13	175.75	-37.22	177.23
NZGD_2000_Bluff_Circuit	2132	New Zealand - South and Stewart Islands - Bluff mc	-47.33	167.29	-45.33	168.97
NZGD_2000_Buller_Circuit	2117	New Zealand - South Island - Buller mc	-42.19	171.27	-41.42	172.41
NZGD_2000_Campbell_Island_TM_2000	3789	New Zealand - Campbell Island	-52.83	168.65	-52.26	169.6
NZGD_2000_Chatham_Island_Circuit	3764	New Zealand - Chatham Islands group	-44.64	-177.25	-43.3	-175.54
NZGD_2000_Chatham_Islands_TM_2000	3793	New Zealand - Chatham Islands group	-44.64	-177.25	-43.3	-175.54
NZGD_2000_Collingwood_Circuit	2114	New Zealand - South Island - Collingwood mc	-41.22	172.16	-40.44	173.13
NZGD_2000_Gawler_Circuit	2125	New Zealand - South Island - Gawler mc	-44.25	170.68	-43.13	172.26
NZGD_2000_Grey_Circuit	2118	New Zealand - South Island - Grey mc	-42.74	171.15	-41.5	172.75
NZGD_2000_Hawkes_Bay_Circuit	2108	New Zealand - North Island - Hawkes Bay mc Napier vcrs	-40.57	175.8	-38.87	178.07
NZGD_2000_Hokitika_Circuit	2121	New Zealand - South Island - Hokitika mc	-43.23	170.39	-42.41	171.89
NZGD_2000_Jacksons_Bay_Circuit	2123	New Zealand - South Island - Jacksons Bay mc	-44.4	168.02	-43.67	170.01
NZGD_2000_Karamea_Circuit	2116	New Zealand - South Island - Karamea mc	-41.49	171.96	-40.75	172.7
NZGD_2000_Lindis_Peak_Circuit	2127	New Zealand - South Island - Lindis Peak mc	-45.4	168.62	-43.71	170.24
NZGD_2000_Marlborough_Circuit	2120	New Zealand - South Island - Marlborough mc	-42.65	172.95	-40.85	174.46
NZGD_2000_Mount_Eden_Circuit	2105	New Zealand - North Island - Mount Eden mc	-39.01	171.99	-34.1	176.12
NZGD_2000_Mount_Nicholas_Circuit	2128	New Zealand - South Island - Mount Nicholas mc	-45.58	167.72	-44.29	169.11
NZGD_2000_Mount_Pleasant_Circuit	2124	New Zealand - South Island - Mount Pleasant mc	-43.96	171.11	-42.69	173.38
NZGD_2000_Mount_York_Circuit	2129	New Zealand - South Island - Mount York mc	-46.33	166.37	-44.53	168.21
NZGD_2000_Nelson_Circuit	2115	New Zealand - South Island - Nelson mc	-42.18	172.4	-40.66	174.08
NZGD_2000_New_Zealand_Transverse_ Mercator	2193	New Zealand - onshore	-47.33	166.37	-34.1	178.63
NZGD_2000_North_Taieri_Circuit	2131	New Zealand - South Island - North Taieri mc	-46.73	168.64	-45.23	170.87
NZGD_2000_NZ_Continental_Shelf_2000	3851	New Zealand - offshore	-55.95	160.6	-25.88	-171.2
NZGD_2000_Observation_Point_Circuit	2130	New Zealand - South Island - Observation Point mc	-45.82	169.77	-44.61	171.24
NZGD_2000_Okarito_Circuit	2122	New Zealand - South Island - Okarito mc	-43.85	169.21	-43	170.89
NZGD_2000_Poverty_Bay_Circuit	2107	New Zealand - North Island - Poverty Bay mc	-39.04	176.73	-37.49	178.63
NZGD_2000_Raoul_Island_TM_2000	3791	New Zealand - Raoul and Kermadec Islands	-31.56	-179.07	-29.03	-177.62
NZGD_2000_Taranaki_Circuit	2109	New Zealand - North Island - Taranaki mc	-39.78	173.68	-38.4	175.44
NZGD_2000_Timaru_Circuit	2126	New Zealand - South Island - Timaru mc	-44.98	169.82	-43.35	171.55
NZGD_2000_Tuhirangi_Circuit	2110	New Zealand - North Island - Tuhirangi mc	-39.55	174.88	-38.87	176.33
NZGD_2000_UTM_Zone_1S	5700	New Zealand - offshore 180°W to 174°W	-52.97	-180	-25.88	-174
NZGD_2000_UTM_Zone_58S	2133	New Zealand - offshore 162°E to168°E	-55.89	162	-39.68	168
NZGD_2000_UTM_Zone_59S	2134	New Zealand - offshore 168°E to 174°E	-55.95	168	-30.78	174
NZGD_2000_UTM_Zone_60S	2135	New Zealand - offshore 174°E to 180°E	-54.32	174	-26.42	180
NZGD_2000_Wairarapa_Circuit	2112	New Zealand - North Island - Wairarapa mc	-41.67	175.01	-40.29	176.55
NZGD_2000_Wanganui_Circuit	2111	New Zealand - North Island - Wanganui mc	-40.97	174.4	-39.46	176.27
NZGD_2000_Wellington_Circuit	2113	New Zealand - North Island - Wellington mc	-41.5	174.52	-40.91	175.36
Observatorio_Meteorologico_1939_UTM _Zone_25N	102166	Portugal - Azores W - onshore	39.3	-31.34	39.77	-31.02
Observatorio_Meteorologico_1965_ Macau_Grid	102159	China - Macao	22.06	113.52	22.23	113.68
Ocotepeque_1935_Costa_Rica_Lambert_ Norte	102221	Costa Rica	2.15	-90.45	11.77	-81.43
Ocotepeque_1935_Costa_Rica_Lambert_ Sur	102222	Costa Rica	2.15	-90.45	11.77	-81.43
Ocotepeque_1935_Costa_Rica_Norte	5456	Costa Rica - onshore north of 9°32'N	9.53	-85.97	11.22	-82.53
Ocotepeque_1935_Costa_Rica_Sur	5457	Costa Rica - onshore south of 9°56'N	7.98	-85.74	9.94	-82.53
Ocotepeque_1935_El_Salvador_Lambert	5460	El Salvador - onshore	13.1	-90.11	14.44	-87.69
Ocotepeque_1935_Guatemala_Norte	5559	Guatemala - north of 15°51'30''N	15.85	-91.86	17.83	-88.34
Ocotepeque_1935_Guatemala_Sur	5459	Guatemala - south of 15°51'30''N	13.69	-92.29	15.86	-88.19
Ocotepeque_1935_Nicaragua_Norte	5461	Nicaragua - onshore north of 12°48'N	12.8	-87.74	15.03	-83.08
Ocotepeque_1935_Nicaragua_Sur	5462	Nicaragua - onshore south of 12°48'N	10.7	-87.63	12.8	-83.42
OCRS_Baker_NAD_1983_2011_TM_Feet_ Intl	6787	USA - Oregon - Baker City	44.6	-118.15	45.19	-117.37
OCRS_Baker_NAD_1983_2011_TM_ Meters	6786	USA - Oregon - Baker City	10.7	-87.63	12.8	-83.42
OCRS_Baker_NAD_1983_CORS96_TM_ Feet_Intl	6785	USA - Oregon - Baker City	44.6	-118.15	45.19	-117.37
OCRS_Baker_NAD_1983_CORS96_TM_ Meters	6784	USA - Oregon - Baker City	10.7	-87.63	12.8	-83.42
OCRS_Bend- Burns_NAD_1983_2011_LCC_Feet_Intl	6799	USA - Oregon - Bend- Burns	43.34	-121.95	44.28	-118.8
OCRS_Bend- Burns_NAD_1983_2011_LCC_Meters	6798	USA - Oregon - Bend- Burns	43.34	-121.95	44.28	-118.8
OCRS_Bend- Burns_NAD_1983_CORS96_LCC_Feet_Intl	6797	USA - Oregon - Bend- Burns	43.34	-121.95	44.28	-118.8
OCRS_Bend- Burns_NAD_1983_CORS96_LCC_Meters	6796	USA - Oregon - Bend- Burns	43.34	-121.95	44.28	-118.8
OCRS_Bend- Klamath_Falls_NAD_1983_2011_TM_ Feet_Intl	6791	USA - Oregon - Bend- Klamath Falls	41.88	-122.45	43.89	-120.77
OCRS_Bend- Klamath_Falls_NAD_1983_2011_TM_ Meters	6790	USA - Oregon - Bend- Klamath Falls	41.88	-122.45	43.89	-120.77
OCRS_Bend-Klamath_Falls_NAD_1983_ CORS96_TM_Feet_Intl	6789	USA - Oregon - Bend- Klamath Falls	41.88	-122.45	43.89	-120.77
OCRS_Bend-Klamath_Falls_NAD_1983_ CORS96_TM_Meters	6788	USA - Oregon - Bend- Klamath Falls	41.88	-122.45	43.89	-120.77
OCRS_Bend-Redmond-Prineville_NAD_ 1983_2011_LCC_Feet_Intl	6795	USA - Oregon - Bend- Redmond-Prineville	43.76	-121.88	44.98	-119.79
OCRS_Bend-Redmond- Prineville_NAD_1983_2011_LCC_Meters	6794	USA - Oregon - Bend- Redmond-Prineville	43.76	-121.88	44.98	-119.79
OCRS_Bend-Redmond-Prineville_NAD _1983_CORS96_LCC_Feet_Intl	6793	USA - Oregon - Bend- Redmond-Prineville	43.76	-121.88	44.98	-119.79
OCRS_Bend-Redmond-Prineville_NAD_ 1983_CORS96_LCC_Meters	6792	USA - Oregon - Bend- Redmond-Prineville	43.76	-121.88	44.98	-119.79
OCRS_Burns-Harper_NAD_1983_ 2011_TM_Ft_Intl	8312	USA - Oregon - Burns- Harper	43.49	-118.61	44.19	-117.49
OCRS_Burns-Harper_NAD_1983_ 2011_TM_Meters	8311	USA - Oregon - Burns- Harper	43.49	-118.61	44.19	-117.49
OCRS_Burns-Harper_NAD_1983_2011_ TM_Ft_Intl	8312	USA - Oregon - Burns- Harper	43.49	-118.61	44.19	-117.49
OCRS_Burns-Harper_NAD_1983_2011_ TM_Meters	8311	USA - Oregon - Burns- Harper	43.49	-118.61	44.19	-117.49
OCRS_Canyonville-Grants_Pass_ NAD_1983_2011_TM_Feet_Intl	6803	USA - Oregon - Canyonville-Grants Pass	42.49	-123.83	43.24	-122.43
OCRS_Canyonville-Grants_Pass_ NAD_1983_2011_TM_Meters	6802	USA - Oregon - Canyonville-Grants Pass	42.49	-123.83	43.24	-122.43
OCRS_Canyonville-Grants_Pass_ NAD_1983_CORS96_TM_Feet_Intl	6801	USA - Oregon - Canyonville-Grants Pass	42.49	-123.83	43.24	-122.43
OCRS_Canyonville-Grants_Pass_ NAD_1983_CORS96_TM_Meters	6800	USA - Oregon - Canyonville-Grants Pass	42.49	-123.83	43.24	-122.43
OCRS_Coast_Range_North_NAD_1983_ 2011_LCC_Ft_Intl	8316	USA - Oregon - Coast Range North	45.4	-123.81	45.98	-123.01
OCRS_Coast_Range_North_NAD_1983_ 2011_LCC_Meters	8315	USA - Oregon - Coast Range North	45.4	-123.81	45.98	-123.01
OCRS_Columbia_River_East_NAD_1983_ 2011_LCC_Feet_Intl	6807	USA - Oregon - Columbia River East	45.49	-122.05	46.08	-118.89
OCRS_Columbia_River_East_NAD_1983_ 2011_LCC_Meters	6806	USA - Oregon - Columbia River East	45.49	-122.05	46.08	-118.89
OCRS_Columbia_River_East_NAD_1983_ CORS96_LCC_Feet_Intl	6805	USA - Oregon - Columbia River East	45.49	-122.05	46.08	-118.89
OCRS_Columbia_River_East_NAD_1983_ CORS96_LCC_Meters	6804	USA - Oregon - Columbia River East	45.49	-122.05	46.08	-118.89
OCRS_Columbia_River_West_NAD_1983_ 2011_OM_Feet_Intl	6811	USA - Oregon - Columbia River West	45.17	-124.33	46.56	-121.47
OCRS_Columbia_River_West_NAD_1983_ 2011_OM_Meters	6810	USA - Oregon - Columbia River West	45.17	-124.33	46.56	-121.47
OCRS_Columbia_River_West_NAD_1983_ CORS96_OM_Feet_Intl	6809	USA - Oregon - Columbia River West	45.17	-124.33	46.56	-121.47
OCRS_Columbia_River_West_NAD_1983_ CORS96_OM_Meters	6808	USA - Oregon - Columbia River West	45.17	-124.33	46.56	-121.47
OCRS_Cottage_Grove-Canyonville_ NAD_1983_2011_TM_Feet_Intl	6815	USA - Oregon - Cottage Grove-Canyonville	42.82	-123.96	43.88	-122.4
OCRS_Cottage_Grove-Canyonville_ NAD_1983_2011_TM_Meters	6814	USA - Oregon - Cottage Grove-Canyonville	42.82	-123.96	43.88	-122.4
OCRS_Cottage_Grove-Canyonville_ NAD_1983_CORS96_TM_Feet_Intl	6813	USA - Oregon - Cottage Grove-Canyonville	42.82	-123.96	43.88	-122.4
OCRS_Cottage_Grove-Canyonville_ NAD_1983_CORS96_TM_Meters	6812	USA - Oregon - Cottage Grove-Canyonville	42.82	-123.96	43.88	-122.4
OCRS_Dayville-Prairie_City_ NAD_1983_2011_TM_Ft_Intl	8318	USA - Oregon - Dayville- Prairie City	44.24	-119.89	44.94	-118.61
OCRS_Dayville-Prairie_City_ NAD_1983_2011_TM_Meters	8317	USA - Oregon - Dayville- Prairie City	44.24	-119.89	44.94	-118.61
OCRS_Denio-Burns_ NAD_1983_2011_TM_Ft_Intl	8320	USA - Oregon - Denio- Burns	41.88	-119.41	43.54	-117.67
OCRS_Denio-Burns_ NAD_1983_2011_TM_Meters	8319	USA - Oregon - Denio- Burns	41.88	-119.41	43.54	-117.67
OCRS_Dufur-Madras_ NAD_1983_2011_TM_Feet_Intl	6819	USA - Oregon - Dufur- Madras	44.63	-121.95	45.55	-120.46
OCRS_Dufur-Madras_ NAD_1983_2011_TM_Meters	6818	USA - Oregon - Dufur- Madras	44.63	-121.95	45.55	-120.46
OCRS_Dufur-Madras_ NAD_1983_CORS96_TM_Feet_Intl	6817	USA - Oregon - Dufur- Madras	44.63	-121.95	45.55	-120.46
OCRS_Dufur-Madras_ NAD_1983_CORS96_TM_Meters	6816	USA - Oregon - Dufur- Madras	44.63	-121.95	45.55	-120.46
OCRS_Eugene_NAD_1983_2011_TM_ Feet_Intl	6823	USA - Oregon - Eugene	43.74	-123.8	44.71	-122.18
OCRS_Eugene_NAD_1983_2011_TM_ Meters	6822	USA - Oregon - Eugene	43.74	-123.8	44.71	-122.18
OCRS_Eugene_NAD_1983_CORS96_TM_ Feet_Intl	6821	USA - Oregon - Eugene	43.74	-123.8	44.71	-122.18
OCRS_Eugene_NAD_1983_CORS96_TM_ Meters	6820	USA - Oregon - Eugene	43.74	-123.8	44.71	-122.18
OCRS_Grants_Pass-Ashland_NAD_1983_ 2011_TM_Feet_Intl	6827	USA - Oregon - Grants Pass-Ashland	41.88	-123.95	42.85	-122.37
OCRS_Grants_Pass-Ashland_NAD_1983_ 2011_TM_Meters	6826	USA - Oregon - Grants Pass-Ashland	41.88	-123.95	42.85	-122.37
OCRS_Grants_Pass-Ashland_NAD_1983_ CORS96_TM_Feet_Intl	6825	USA - Oregon - Grants Pass-Ashland	41.88	-123.95	42.85	-122.37
OCRS_Grants_Pass-Ashland_NAD_1983_ CORS96_TM_Meters	6824	USA - Oregon - Grants Pass-Ashland	41.88	-123.95	42.85	-122.37
OCRS_Gresham-Warm_Springs_ NAD_1983_2011_TM_Feet_Intl	6831	USA - Oregon - Gresham-Warm Springs	45.02	-122.43	45.55	-121.68
OCRS_Gresham-Warm_Springs_ NAD_1983_2011_TM_Meters	6830	USA - Oregon - Gresham-Warm Springs	45.02	-122.43	45.55	-121.68
OCRS_Gresham-Warm_Springs_ NAD_1983_CORS96_TM_Feet_Intl	6829	USA - Oregon - Gresham-Warm Springs	45.02	-122.43	45.55	-121.68
OCRS_Gresham-Warm_Springs_ NAD_1983_CORS96_TM_Meters	6828	USA - Oregon - Gresham-Warm Springs	45.02	-122.43	45.55	-121.68
OCRS_Halfway_NAD_1983_2011_LCC_ Ft_Intl	8322	USA - Oregon - Halfway	44.61	-117.61	45.28	-116.63
OCRS_Halfway_NAD_1983_2011_LCC_ Meters	8321	USA - Oregon - Halfway	44.61	-117.61	45.28	-116.63
OCRS_La_Grande_NAD_1983_2011_TM_ Feet_Intl	6835	USA - Oregon - La Grande	45.13	-118.17	45.8	-117.14
OCRS_La_Grande_NAD_1983_2011_TM_ Meters	6834	USA - Oregon - La Grande	45.13	-118.17	45.8	-117.14
OCRS_La_Grande_NAD_1983_CORS96_ TM_Feet_Intl	6833	USA - Oregon - La Grande	45.13	-118.17	45.8	-117.14
OCRS_La_Grande_NAD_1983_CORS96_ TM_Meters	6832	USA - Oregon - La Grande	45.13	-118.17	45.8	-117.14
OCRS_Medford-Diamond_Lake_ NAD_1983_2011_LCC_Ft_Intl	8324	USA - Oregon - Medford-Diamond Lake	42.53	-122.73	43.34	-121.71
OCRS_Medford-Diamond_Lake_ NAD_1983_2011_LCC_Meters	8323	USA - Oregon - Medford-Diamond Lake	42.53	-122.73	43.34	-121.71
OCRS_Mitchell_NAD_1983_2011_LCC_ Ft_Intl	8326	USA - Oregon - Mitchell	44.38	-120.56	44.78	-119.82
OCRS_Mitchell_NAD_1983_2011_LCC_ Meters	8325	USA - Oregon - Mitchell	44.38	-120.56	44.78	-119.82
OCRS_North_Central_NAD_1983_2011_ LCC_Ft_Intl	8328	USA - Oregon - North Central	44.89	-121.79	45.95	-119.03
OCRS_North_Central_NAD_1983_2011_ LCC_Meters	8327	USA - Oregon - North Central	44.89	-121.79	45.95	-119.03
OCRS_Ochoco_Summit_NAD_1983_2011 _LCC_Ft_Intl	8330	USA - Oregon - Ochoco Summit	44.21	-121.01	44.61	-120.31
OCRS_Ochoco_Summit_NAD_1983_2011 _LCC_Meters	8329	USA - Oregon - Ochoco Summit	44.21	-121.01	44.61	-120.31
OCRS_Ontario_NAD_1983_2011_TM_ Feet_Intl	6839	USA - Oregon - Ontario	43.41	-117.9	44.65	-116.7
OCRS_Ontario_NAD_1983_2011_TM_ Meters	6838	USA - Oregon - Ontario	43.41	-117.9	44.65	-116.7
OCRS_Ontario_NAD_1983_CORS96_TM_ Feet_Intl	6837	USA - Oregon - Ontario	43.41	-117.9	44.65	-116.7
OCRS_Ontario_NAD_1983_CORS96_TM_ Meters	6836	USA - Oregon - Ontario	43.41	-117.9	44.65	-116.7
OCRS_Oregon_Coast_NAD_1983_2011_ OM_Feet_Intl	6843	USA - Oregon - Oregon Coast	41.89	-124.84	46.4	-123.35
OCRS_Oregon_Coast_NAD_1983_2011_ OM_Meters	6842	USA - Oregon - Oregon Coast	41.89	-124.84	46.4	-123.35
OCRS_Oregon_Coast_NAD_1983_CORS96 _OM_Feet_Intl	6841	USA - Oregon - Oregon Coast	41.89	-124.84	46.4	-123.35
OCRS_Oregon_Coast_NAD_1983_CORS96 _OM_Meters	6840	USA - Oregon - Oregon Coast	41.89	-124.84	46.4	-123.35
OCRS_Owyhee_NAD_1983_2011_TM_ Ft_Intl	8332	USA - Oregon - Owyhee	41.88	-118.14	43.54	-116.85
OCRS_Owyhee_NAD_1983_2011_TM_ Meters	8331	USA - Oregon - Owyhee	41.88	-118.14	43.54	-116.85
OCRS_Pendleton-La_Grande_NAD_1983_ 2011_TM_Feet_Intl	6851	USA - Oregon - Pendleton-La Grande	45.13	-118.64	45.64	-118.09
OCRS_Pendleton-La_Grande_NAD_1983_ 2011_TM_Meters	6850	USA - Oregon - Pendleton-La Grande	45.13	-118.64	45.64	-118.09
OCRS_Pendleton-La_Grande_NAD_1983_ CORS96_TM_Feet_Intl	6849	USA - Oregon - Pendleton-La Grande	45.13	-118.64	45.64	-118.09
OCRS_Pendleton-La_Grande_NAD_1983_ CORS96_TM_Meters	6848	USA - Oregon - Pendleton-La Grande	45.13	-118.64	45.64	-118.09
OCRS_Pendleton_NAD_1983_2011_TM_ Feet_Intl	6847	USA - Oregon - Pendleton	45.46	-119.36	46.02	-118.17
OCRS_Pendleton_NAD_1983_2011_TM_ Meters	6846	USA - Oregon - Pendleton	45.46	-119.36	46.02	-118.17
OCRS_Pendleton_NAD_1983_CORS96_ TM_Feet_Intl	6845	USA - Oregon - Pendleton	45.46	-119.36	46.02	-118.17
OCRS_Pendleton_NAD_1983_CORS96_ TM_Meters	6844	USA - Oregon - Pendleton	45.46	-119.36	46.02	-118.17
OCRS_Pilot_Rock-Ukiah_NAD_1983_ 2011_LCC_Ft_Intl	8334	USA - Oregon - Pilot Rock-Ukiah	44.99	-119.65	46.04	-118.11
OCRS_Pilot_Rock-Ukiah_NAD_1983_ 2011_LCC_Meters	8333	USA - Oregon - Pilot Rock-Ukiah	44.99	-119.65	46.04	-118.11
OCRS_Portland_NAD_1983_2011_LCC_ Feet_Intl	6855	USA - Oregon - Portland	45.23	-123.53	46.01	-122.11
OCRS_Portland_NAD_1983_2011_LCC_ Meters	6854	USA - Oregon - Portland	45.12	45.23	-123.53	46.01
OCRS_Portland_NAD_1983_CORS96_LCC _Feet_Intl	6853	USA - Oregon - Portland	45.12	45.23	-123.53	46.01
OCRS_Portland_NAD_1983_CORS96_LCC _Meters	6852	USA - Oregon - Portland	45.12	45.23	-123.53	46.01
OCRS_Prairie_City-Brogan_NAD_1983_ 2011_LCC_Ft_Intl	8336	USA - Oregon - Prairie City-Brogan	44.16	-118.77	45.02	-117.48
OCRS_Prairie_City-Brogan_NAD_1983_ 2011_LCC_Meters	8335	USA - Oregon - Prairie City-Brogan	44.16	-118.77	45.02	-117.48
OCRS_Riley-Lakeview_NAD_1983_ 2011_TM_Ft_Intl	8338	USA - Oregon - Riley- Lakeview	41.88	-120.97	43.45	-119.15
OCRS_Riley-Lakeview_NAD_1983_ 2011_TM_Meters	8337	USA - Oregon - Riley- Lakeview	41.88	-120.97	43.45	-119.15
OCRS_Salem_NAD_1983_2011_TM_Feet _Intl	6859	USA - Oregon - Salem	44.32	-123.73	45.3	-121.89
OCRS_Salem_NAD_1983_2011_TM_ Meters	6858	USA - Oregon - Salem	44.32	-123.73	45.3	-121.89
OCRS_Salem_NAD_1983_CORS96_TM_ Feet_Intl	6857	USA - Oregon - Salem	44.32	-123.73	45.3	-121.89
OCRS_Salem_NAD_1983_CORS96_TM_ Meters	6856	USA - Oregon - Salem	44.32	-123.73	45.3	-121.89
OCRS_Santiam_Pass_NAD_1983_2011_ TM_Feet_Intl	6863	USA - Oregon - Sweet Home-Sisters	44.11	-122.51	44.66	-121.69
OCRS_Santiam_Pass_NAD_1983_2011_ TM_Meters	6862	USA - Oregon - Sweet Home-Sisters	44.11	-122.51	44.66	-121.69
OCRS_Santiam_Pass_NAD_1983_CORS96 _TM_Feet_Intl	6861	USA - Oregon - Sweet Home-Sisters	44.11	-122.51	44.66	-121.69
OCRS_Santiam_Pass_NAD_1983_CORS96 _TM_Meters	6860	USA - Oregon - Sweet Home-Sisters	44.11	-122.51	44.66	-121.69
OCRS_Siskiyou_Pass_NAD_1983_2011_ LCC_Ft_Intl	8340	USA - Oregon - Siskiyou Pass	41.95	-122.71	42.46	-121.96
OCRS_Siskiyou_Pass_NAD_1983_2011_ LCC_Meters	8339	USA - Oregon - Siskiyou Pass	41.95	-122.71	42.46	-121.96
OCRS_Ukiah-Fox_NAD_1983_2011_ LCC_Ft_Intl	8342	USA - Oregon - Ukiah- Fox	44.52	-119.35	45.21	-118.64
OCRS_Ukiah-Fox_NAD_1983_2011_ LCC_Meters	8341	USA - Oregon - Ukiah- Fox	44.52	-119.35	45.21	-118.64
OCRS_Wallowa_NAD_1983_2011_TM_ Ft_Intl	8344	USA - Oregon - Wallowa	45.27	-118.16	46.05	-116.42
OCRS_Wallowa_NAD_1983_2011_TM_ Meters	8343	USA - Oregon - Wallowa	45.27	-118.16	46.05	-116.42
OCRS_Warner_Highway_NAD_1983_ 2011_LCC_Ft_Intl	8346	USA - Oregon - Warner Highway	41.95	-120.42	42.43	-119.3
OCRS_Warner_Highway_NAD_1983_ 2011_LCC_Meters	8345	USA - Oregon - Warner Highway	41.95	-120.42	42.43	-119.3
OCRS_Willamette_Pass_NAD_1983_2011 _TM_Ft_Intl	8348	USA - Oregon - Willamette Pass	42.99	-122.26	44.18	-121.48
OCRS_Willamette_Pass_NAD_1983_2011 _TM_Meters	8347	USA - Oregon - Willamette Pass	42.99	-122.26	44.18	-121.48
Old_Hawaiian_StatePlane_Hawaii_1_FIPS _5101	3561	USA - Hawaii - island of Hawaii - onshore	18.87	-156.1	20.33	-154.74
Old_Hawaiian_StatePlane_Hawaii_2_FIPS _5102	3562	USA - Hawaii - Maui; Kahoolawe; Lanai; Molokai - onshore	20.45	-157.36	21.26	-155.93
Old_Hawaiian_StatePlane_Hawaii_3_FIPS _5103	3563	USA - Hawaii - Oahu - onshore	21.2	-158.33	21.75	-157.61
Old_Hawaiian_StatePlane_Hawaii_4_FIPS _5104	3564	USA - Hawaii - Kauai - onshore	21.81	-159.85	22.29	-159.23
Old_Hawaiian_StatePlane_Hawaii_5_FIPS _5105	3565	USA - Hawaii - Niihau - onshore	21.73	-160.3	22.07	-159.99
Old_Hawaiian_UTM_Zone_4N	102114	USA - 162°W to 156°W onshore - HI	19.51	-160.3	22.29	-156
Old_Hawaiian_UTM_Zone_5N	102115	USA - 156°W to 150°W onshore - HI	18.87	-156	20.86	-154.74
ONGD14_UTM_Zone_39N	7374	Oman - west of 54°E	14.94	51.99	19.67	54.01
ONGD14_UTM_Zone_40N	7375	Oman - 54°E to 60°E	14.33	54	26.74	60.01
ONGD14_UTM_Zone_41N	7376	Oman - east of 60°E	16.37	60	24.09	63.38
ONGD17_UTM_Zone_39N	9295	Oman - west of 54°E	14.94	51.99	19.67	54.01
ONGD17_UTM_Zone_40N	9296	Oman - 54°E to 60°E	14.33	54	26.74	60.01
ONGD17_UTM_Zone_41N	9297	Oman - east of 60°E	16.37	60	24.09	63.38
OSNI_1952_Irish_National_Grid	29901	UK - Northern Ireland - onshore	53.96	-8.18	55.36	-5.34
OSGB36_Highways_England_A10H1	102814	UK - Highways England - A10	50.228	-4.314	50.807	-4.089
OSGB36_Highways_England_A10H2	102815	UK - Highways England - A10	50.228	-4.314	50.807	-4.089
OSGB36_Highways_England_A11H1	102816	UK - Highways England - A11	50.231	-4.115	50.81	-3.879
OSGB36_Highways_England_A11H2	102817	UK - Highways England - A11	50.231	-4.115	50.81	-3.879
OSGB36_Highways_England_A11H3	102818	UK - Highways England - A11	50.231	-4.115	50.81	-3.879
OSGB36_Highways_England_A12H1	102819	UK - Highways England - A12	50.235	-3.902	50.814	-3.655
OSGB36_Highways_England_A12H2	102820	UK - Highways England - A12	50.235	-3.902	50.814	-3.655
OSGB36_Highways_England_A12H3	102821	UK - Highways England - A12	50.235	-3.902	50.814	-3.655
OSGB36_Highways_England_A13H1	102822	UK - Highways England - A13	50.418	-3.678	50.898	-3.422
OSGB36_Highways_England_A13H2	102823	UK - Highways England - A13	50.418	-3.678	50.898	-3.422
OSGB36_Highways_England_A14H1	102824	UK - Highways England - A14	50.585	-4.447	51.198	-3.102
OSGB36_Highways_England_A14H2	102825	UK - Highways England - A14	50.585	-4.447	51.198	-3.102
OSGB36_Highways_England_A15H1	102826	UK - Highways England - A15	50.605	-3.138	52.047	-2.622
OSGB36_Highways_England_A15H2	102827	UK - Highways England - A15	50.605	-3.138	52.047	-2.622
OSGB36_Highways_England_A16H1	102828	UK - Highways England - A16	50.608	-2.642	52.048	-1.504
OSGB36_Highways_England_A16H2	102829	UK - Highways England - A16	50.608	-2.642	52.048	-1.504
OSGB36_Highways_England_A17H1	102830	UK - Highways England - A17	50.777	-1.518	52.048	-1.008
OSGB36_Highways_England_A17H2	102831	UK - Highways England - A17	50.777	-1.518	52.048	-1.008
OSGB36_Highways_England_A18H1	102832	UK - Highways England - A18	50.773	-1.036	52.045	-0.571
OSGB36_Highways_England_A18H2	102833	UK - Highways England - A18	50.773	-1.036	52.045	-0.571
OSGB36_Highways_England_A19H1	102834	UK - Highways England - A19	50.77	-0.61	52.04	-0.323
OSGB36_Highways_England_A19H2	102835	UK - Highways England - A19	50.77	-0.61	52.04	-0.323
OSGB36_Highways_England_A1H1	102799	UK - Highways England - A1	50.107	-5.548	50.425	-5.399
OSGB36_Highways_England_A20H1	102836	UK - Highways England - A20	50.766	-0.369	52.037	-0.075
OSGB36_Highways_England_A20H2	102837	UK - Highways England - A20	50.766	-0.369	52.037	-0.075
OSGB36_Highways_England_A21H1	102838	UK - Highways England - A21	50.762	-0.128	52.033	0.172
OSGB36_Highways_England_A21H2	102839	UK - Highways England - A21	50.762	-0.128	52.033	0.172
OSGB36_Highways_England_A22H1	102840	UK - Highways England - A22	50.757	0.113	52.029	0.42
OSGB36_Highways_England_A22H2	102841	UK - Highways England - A22	50.757	0.113	52.029	0.42
OSGB36_Highways_England_A23H1	102842	UK - Highways England - A23	50.755	0.354	52.024	0.551
OSGB36_Highways_England_A23H2	102843	UK - Highways England - A23	50.755	0.354	52.024	0.551
OSGB36_Highways_England_A24H1	102844	UK - Highways England - A24	50.751	0.481	52.021	0.711
OSGB36_Highways_England_A24H2	102845	UK - Highways England - A24	50.751	0.481	52.021	0.711
OSGB36_Highways_England_A25H1	102846	UK - Highways England - A25	50.748	0.637	52.018	0.857
OSGB36_Highways_England_A25H2	102847	UK - Highways England - A25	50.748	0.637	52.018	0.857
OSGB36_Highways_England_A26H1	102848	UK - Highways England - A26	50.744	0.779	52.014	1.002
OSGB36_Highways_England_A26H2	102849	UK - Highways England - A26	50.744	0.779	52.014	1.002
OSGB36_Highways_England_A27H1	102850	UK - Highways England - A27	50.929	0.932	52.011	1.148
OSGB36_Highways_England_A27H2	102851	UK - Highways England - A27	50.929	0.932	52.011	1.148
OSGB36_Highways_England_A28H1	102852	UK - Highways England - A28	50.926	1.074	52.007	1.279
OSGB36_Highways_England_A28H2	102853	UK - Highways England - A28	50.926	1.074	52.007	1.279
OSGB36_Highways_England_A29H1	102854	UK - Highways England - A29	50.922	1.202	52.003	1.409
OSGB36_Highways_England_A2H1	102800	UK - Highways England - A2	50.111	-5.422	50.429	-5.273
OSGB36_Highways_England_A30H1	102855	UK - Highways England - A30	50.919	1.33	52	1.54
OSGB36_Highways_England_A3H1	102801	UK - Highways England - A3	50.114	-5.295	50.432	-5.148
OSGB36_Highways_England_A3H2	102802	UK - Highways England - A3	50.114	-5.295	50.432	-5.148
OSGB36_Highways_England_A4H1	102803	UK - Highways England - A4	50.208	-5.175	50.525	-5.028
OSGB36_Highways_England_A5H1	102804	UK - Highways England - A5	50.211	-5.048	50.529	-4.888
OSGB36_Highways_England_A5H2	102805	UK - Highways England - A5	50.211	-5.048	50.529	-4.888
OSGB36_Highways_England_A6H1	102806	UK - Highways England - A6	50.214	-4.907	50.532	-4.748
OSGB36_Highways_England_A6H2	102807	UK - Highways England - A6	50.214	-4.907	50.532	-4.748
OSGB36_Highways_England_A7H1	102808	UK - Highways England - A7	50.398	-4.766	50.536	-4.617
OSGB36_Highways_England_A7H2	102809	UK - Highways England - A7	50.398	-4.766	50.536	-4.617
OSGB36_Highways_England_A8H1	102810	UK - Highways England - A8	50.221	-4.64	50.8	-4.454
OSGB36_Highways_England_A8H2	102811	UK - Highways England - A8	50.221	-4.64	50.8	-4.454
OSGB36_Highways_England_A9H1	102812	UK - Highways England - A9	50.224	-4.484	50.803	-4.285
OSGB36_Highways_England_A9H2	102813	UK - Highways England - A9	50.224	-4.484	50.803	-4.285
OSGB36_Highways_England_B15H1	102856	UK - Highways England - B15	52.043	-3.188	53.935	-2.642
OSGB36_Highways_England_B15H2	102857	UK - Highways England - B15	52.043	-3.188	53.935	-2.642
OSGB36_Highways_England_B15H3	102858	UK - Highways England - B15	52.043	-3.188	53.935	-2.642
OSGB36_Highways_England_B16H1	102859	UK - Highways England - B16	52.047	-2.67	53.936	-1.482
OSGB36_Highways_England_B16H2	102860	UK - Highways England - B16	52.047	-2.67	53.936	-1.482
OSGB36_Highways_England_B16H3	102861	UK - Highways England - B16	52.047	-2.67	53.936	-1.482
OSGB36_Highways_England_B16H4	102862	UK - Highways England - B16	52.047	-2.67	53.936	-1.482
OSGB36_Highways_England_B17H1	102863	UK - Highways England - B17	52.045	-1.504	53.936	-0.964
OSGB36_Highways_England_B17H2	102864	UK - Highways England - B17	52.045	-1.504	53.936	-0.964
OSGB36_Highways_England_B18H1	102865	UK - Highways England - B18	52.04	-1.008	53.932	-0.507
OSGB36_Highways_England_B18H2	102866	UK - Highways England - B18	52.04	-1.008	53.932	-0.507
OSGB36_Highways_England_B19H1	102867	UK - Highways England - B19	52.037	-0.571	53.928	-0.249
OSGB36_Highways_England_B20H1	102868	UK - Highways England - B20	52.033	-0.323	53.924	0.01
OSGB36_Highways_England_B21H1	102869	UK - Highways England - B21	52.029	-0.076	52.806	0.21
OSGB36_Highways_England_B22H1	102870	UK - Highways England - B22	52.024	0.172	52.802	0.463
OSGB36_Highways_England_B23H1	102871	UK - Highways England - B23	52.021	0.42	52.797	0.596
OSGB36_Highways_England_B24H1	102872	UK - Highways England - B24	52.018	0.551	52.794	0.759
OSGB36_Highways_England_B25H1	102873	UK - Highways England - B25	52.014	0.711	52.79	0.907
OSGB36_Highways_England_B26H1	102874	UK - Highways England - B26	52.011	0.857	52.787	1.055
OSGB36_Highways_England_B27H1	102875	UK - Highways England - B27	52.007	1.002	52.783	1.203
OSGB36_Highways_England_B28H1	102876	UK - Highways England - B28	52.003	1.148	52.779	1.336
OSGB36_Highways_England_B29H1	102877	UK - Highways England - B29	52	1.278	52.775	1.47
OSGB36_Highways_England_B30H1	102878	UK - Highways England - B30	51.996	1.409	52.772	1.603
OSGB36_Highways_England_B31H1	102879	UK - Highways England - B31	52.342	1.568	52.767	1.736
OSGB36_Highways_England_B32H1	102880	UK - Highways England - B32	52.337	1.7	52.763	1.869
OSGB36_Highways_England_C13H1	102881	UK - Highways England - C13	54.364	-3.834	54.772	-3.555
OSGB36_Highways_England_C14H1	102882	UK - Highways England - C14	54.008	-3.57	54.776	-3.19
OSGB36_Highways_England_C14H2	102883	UK - Highways England - C14	54.008	-3.57	54.776	-3.19
OSGB36_Highways_England_C14H3	102884	UK - Highways England - C14	54.008	-3.57	54.776	-3.19
OSGB36_Highways_England_C14H4	102885	UK - Highways England - C14	54.008	-3.57	54.776	-3.19
OSGB36_Highways_England_C15H1	102886	UK - Highways England - C15	53.931	-3.224	55.139	-2.67
OSGB36_Highways_England_C15H2	102887	UK - Highways England - C15	53.931	-3.224	55.139	-2.67
OSGB36_Highways_England_C15H3	102888	UK - Highways England - C15	53.931	-3.224	55.139	-2.67
OSGB36_Highways_England_C15H4	102889	UK - Highways England - C15	53.931	-3.224	55.139	-2.67
OSGB36_Highways_England_C15H5	102890	UK - Highways England - C15	53.931	-3.224	55.139	-2.67
OSGB36_Highways_England_C16H1	102891	UK - Highways England - C16	53.935	-2.703	55.832	-1.457
OSGB36_Highways_England_C16H2	102892	UK - Highways England - C16	53.935	-2.703	55.832	-1.457
OSGB36_Highways_England_C16H3	102893	UK - Highways England - C16	53.935	-2.703	55.832	-1.457
OSGB36_Highways_England_C16H4	102894	UK - Highways England - C16	53.935	-2.703	55.832	-1.457
OSGB36_Highways_England_C17H1	102895	UK - Highways England - C17	53.932	-1.482	55.518	-0.923
OSGB36_Highways_England_C17H2	102896	UK - Highways England - C17	53.932	-1.482	55.518	-0.923
OSGB36_Highways_England_C18H1	102897	UK - Highways England - C18	53.928	-0.964	54.391	-0.491
OSGB36_Highways_England_C18H2	102898	UK - Highways England - C18	53.928	-0.964	54.391	-0.491
OSGB36_Highways_England_C19H1	102899	UK - Highways England - C19	53.924	-0.507	54.386	-0.229
OSGB36_Highways_England_C19H2	102900	UK - Highways England - C19	53.924	-0.507	54.386	-0.229
Palestine_Grid_1923_Modified_TM	103699	Palestine Territory	31.21	34.17	32.55	35.58
Palestine_1923_Israel_CS_Grid	28193	Asia - Middle East - Israel and Palestine Territory onshore	29.45	34.17	33.28	35.69
Palestine_1923_Palestine_Belt	28192	Asia - Middle East - Israel, Jordan and Palestine onshore	29.18	34.17	33.38	39.31
Palestine_1923_Palestine_Grid	28191	Asia - Middle East - Israel, Jordan and Palestine onshore	29.18	34.17	33.38	39.31
Palestine_1923_Palestine_Grid_TM	7142	Asia - Middle East - Israel, Jordan and Palestine onshore	29.18	34.17	33.38	39.31
Pampa_del_Castillo_Argentina_1	9284	Argentina - 42.5°S to 50.3°S and west of 70.5°W	-50.34	-73.59	-44.94	-70.5
Pampa_del_Castillo_Argentina_2	2082	Argentina - 42.5°S to 50.3°S and 70.5°W to 67.5°W	-50.34	-70.5	-42.49	-67.49
Pampa_del_Castillo_Argentina_3	9285	Argentina - 42.5°S to 50.3°S and east of 67.5°W	-49.05	-67.5	-43.58	-65.47
Panama-Colon_1911_Panama_Lambert	5469	Panama - onshore	7.15	-83.04	9.68	-77.19
Panama-Colon_1911_Panama_Polyconic	5472	Panama - onshore	7.15	-83.04	9.68	-77.19
Panhandle_Energy_Albers	102589	USA - Contiguous US	20	-125	50	-65
PD/83_3_Degree_GK_Zone_3_E-N	5666	Germany - Thuringen - west of 10.5°E	50.35	9.92	51.56	10.5
PD/83_3_Degree_GK_Zone_4_E-N	5667	Germany - Thuringen - east of 10.5°E	50.2	10.5	51.64	12.56
PD/83_GK_Zone_3	3396	Germany - Thuringen - west of 10.5°E	50.35	9.92	51.56	10.5
PD/83_GK_Zone_4	3397	Germany - Thuringen - east of 10.5°E	50.2	10.5	51.64	12.56
PDO_1993_UTM_Zone_39N	3439	Oman - onshore west of 54°E	16.59	51.99	19.67	54
PDO_1993_UTM_Zone_40N	3440	Oman - onshore east of 54°E	16.89	54	26.58	59.91
Perroud_1950_Terre_Adelie_Polar_ Stereographic	2986	Antarctica - Adelie Land coastal area	-67.13	136	-65.61	142
Peru96_UTM_Zone_17S	5839	Peru - 84°W to 78°W	-17.33	-84	-3.11	-78
Peru96_UTM_Zone_18S	5387	Peru - 78°W to 72°W	-21.05	-78	-0.03	-72
Peru96_UTM_Zone_19S	5389	Peru - east of 72°W	-20.44	-72	-2.14	-68.67
Peru_Central_Zone	24892	Peru - 79°W to 73°W	-16.57	-79	-0.03	-73
Peru_East_Zone	24893	Peru - east of 73°W	-18.39	-73	-2.14	-68.67
Peru_West_Zone	24891	Peru - west of 79°W	-8.32	-81.41	-3.38	-79
Petrels_1972_Terre_Adelie_Polar_ Stereographic	2985	Antarctica - Adelie Land - Petrels island	-66.78	139.44	-66.1	141.5
Philippines_Zone_I	25391	Philippines - zone I onshore	7.75	116.89	9.32	118
Philippines_Zone_II	25392	Philippines - zone II onshore	8.82	118	11.58	120.07
Philippines_Zone_III	25393	Philippines - zone III onshore	4.99	119.7	19.45	122.21
Philippines_Zone_IV	25394	Philippines - zone IV onshore	6.35	121.74	18.58	124.29
Philippines_Zone_V	25395	Philippines - zone V onshore	5.5	123.73	14.15	126.65
Pitcairn_1967_UTM_Zone_9S	3784	Pitcairn - Pitcairn Island	-25.14	-130.16	-25	-130.01
Pitcairn_2006_Pitcairn_TM_2006	3783	Pitcairn - Pitcairn Island	-25.14	-130.16	-25	-130.01
PNG94_PNGMG94_Zone_54	5550	Papua New Guinea - west of 144°E	-11.15	139.2	2.31	144
PNG94_PNGMG94_Zone_55	5551	Papua New Guinea - 144°E to 150°E	-13.88	144	2.58	150.01
PNG94_PNGMG94_Zone_56	5552	Papua New Guinea - 150°E to 156°E	-14.75	150	1.98	156
Pohnpei_Az_Eq_1971	102237	Micronesia	-1.19	135.27	13.43	165.68
Pointe_Noire_UTM_Zone_32S	28232	Congo	-6.91	8.84	3.72	18.65
Porto_Santo_1936_UTM_Zone_28N	2942	Portugal - Madeira archipelago onshore	32.35	-17.31	33.15	-16.23
Porto_Santo_1995_UTM_Zone_28N	3061	Portugal - Madeira archipelago onshore	32.35	-17.31	33.15	-16.23
Portuguese_National_Grid	20790	Portugal - mainland - onshore	36.95	-9.56	42.16	-6.19
POSGAR_1994_Argentina_Zone_1	22181	Argentina - west of 70.5°W	-52	-73.59	-36.16	-70.5
POSGAR_1994_Argentina_Zone_2	22182	Argentina - 70.5°W to 67.5°W onshore	-54.9	-70.5	-24.08	-67.49
POSGAR_1994_Argentina_Zone_3	22183	Argentina - 67.5°W to 64.5°W onshore	-55.11	-67.5	-21.78	-64.49
POSGAR_1994_Argentina_Zone_4	22184	Argentina - 64.5°W to 61.5°W onshore	-54.91	-64.5	-21.99	-61.5
POSGAR_1994_Argentina_Zone_5	22185	Argentina - 61.5°W to 58.5°W onshore	-39.06	-61.51	-23.37	-58.5
POSGAR_1994_Argentina_Zone_6	22186	Argentina - 58.5°W to 55.5°W onshore	-38.59	-58.5	-24.84	-55.49
POSGAR_1994_Argentina_Zone_7	22187	Argentina - east of 55.5°W onshore	-28.11	-55.5	-25.49	-53.65
POSGAR_1998_Argentina_Zone_1	22171	Argentina - west of 70.5°W	-52	-73.59	-36.16	-70.5
POSGAR_1998_Argentina_Zone_2	22172	Argentina - 70.5°W to 67.5°W onshore	-54.9	-70.5	-24.08	-67.49
POSGAR_1998_Argentina_Zone_3	22173	Argentina - 67.5°W to 64.5°W onshore	-55.11	-67.5	-21.78	-64.49
POSGAR_1998_Argentina_Zone_4	22174	Argentina - 64.5°W to 61.5°W onshore	-54.91	-64.5	-21.99	-61.5
POSGAR_1998_Argentina_Zone_5	22175	Argentina - 61.5°W to 58.5°W onshore	-39.06	-61.51	-23.37	-58.5
POSGAR_1998_Argentina_Zone_6	22176	Argentina - 58.5°W to 55.5°W onshore	-38.59	-58.5	-24.84	-55.49
POSGAR_1998_Argentina_Zone_7	22177	Argentina - east of 55.5°W onshore	-28.11	-55.5	-25.49	-53.65
POSGAR_2007_Argentina_Zone_1	5343	Argentina - west of 70.5°W	-52	-73.59	-36.16	-70.5
POSGAR_2007_Argentina_Zone_2	5344	Argentina - 70.5°W to 67.5°W onshore	-54.9	-70.5	-24.08	-67.49
POSGAR_2007_Argentina_Zone_3	5345	Argentina - 67.5°W to 64.5°W onshore	-55.11	-67.5	-21.78	-64.49
POSGAR_2007_Argentina_Zone_4	5346	Argentina - 64.5°W to 61.5°W onshore	-54.91	-64.5	-21.99	-61.5
POSGAR_2007_Argentina_Zone_5	5347	Argentina - 61.5°W to 58.5°W onshore	-39.06	-61.51	-23.37	-58.5
POSGAR_2007_Argentina_Zone_6	5348	Argentina - 58.5°W to 55.5°W onshore	-38.59	-58.5	-24.84	-55.49
POSGAR_2007_Argentina_Zone_7	5349	Argentina - east of 55.5°W onshore	-28.11	-55.5	-25.49	-53.65
POSGAR_2007_CABA_2019	9498	Argentina - Buenos Aires city	-34.71	-58.54	-34.5	-58.29
POSGAR_2007_UTM_zone_19S	9265	Argentina - Tierra del Fuego offshore west of 66°W	-54.61	-68.62	-51.65	-66
Prince_Edward_Island_Stereographic	2290	Canada - Prince Edward Island	45.9	-64.49	47.09	-61.9
PRS_1992_Philippines_Zone_I	3121	Philippines - zone I	6.21	116.04	18.64	118
PRS_1992_Philippines_Zone_II	3122	Philippines - zone II	3.02	118	20.42	120.07
PRS_1992_Philippines_Zone_III	3123	Philippines - zone III	3	119.7	21.62	122.21
PRS_1992_Philippines_Zone_IV	3124	Philippines - zone IV	3.44	121.74	22.18	124.29
PRS_1992_Philippines_Zone_V	3125	Philippines - zone V	4.76	123.73	21.97	126.65
PRS_1992_UTM_Zone_50N	102456	Philippines - West of 120°E, N hemisphere	3	114	22	120
PRS_1992_UTM_Zone_51N	102457	Philippines - 120°E to 126°E, N hemisphere	3	120	24	126
PRS_1992_UTM_Zone_52N	102458	Philippines - East of 126°E, N hemisphere	4	126	20	132
PSAD_1956_ICN_Regional	2317	Venezuela - onshore	0.64	-73.38	12.25	-59.8
PSAD_1956_UTM_Zone_17N	24817	South America - 84°W to 78°W, N hemisphere and PSAD56 by country	0	-80.18	1.45	-78
PSAD_1956_UTM_Zone_17S	24877	South America - 84°W to 78°W, S hemisphere and PSAD56 by country	-10.53	-81.41	0	-78
PSAD_1956_UTM_Zone_18N	24818	South America - 78°W to 72°W, N hemisphere and PSAD56 by country	0	-78	11.62	-71.99
PSAD_1956_UTM_Zone_18S	24878	South America - 78°W to 72°W, S hemisphere and PSAD56 by country	-43.5	-78	0	-71.99
PSAD_1956_UTM_Zone_19N	24819	South America - 72°W to 66°W, N hemisphere and PSAD56 by country	0.73	-72	12.68	-66
PSAD_1956_UTM_Zone_19S	24879	South America - 72°W to 66°W, S hemisphere and PSAD56 by country	-43.5	-72	-2.14	-66
PSAD_1956_UTM_Zone_20N	24820	South America - 66°W to 60°W, N hemisphere and PSAD56 by country	0.64	-66	11.23	-59.99
PSAD_1956_UTM_Zone_20S	24880	Bolivia - 66°W to 60°W	-22.87	-66	-9.67	-60
PSAD_1956_UTM_Zone_21N	24821	South America - 60°W to 54°W, N hemisphere and PSAD56 by country	1.18	-60	8.58	-56.47
PSAD_1956_UTM_Zone_21S	24881	Bolivia - east of 60°W	-20.17	-60	-16.27	-57.52
PSAD_1956_UTM_Zone_22S	24882	Brazil - Amazon cone shelf	-1.05	-51.64	5.6	-48
PTRA08_LAEA_Europe	5633	Portugal - Azores and Madeira	29.24	-35.58	43.07	-12.48
PTRA08_LCC_Europe	5632	Portugal - Azores and Madeira	29.24	-35.58	43.07	-12.48
PTRA08_UTM_Zone_25N	5014	Portugal - Azores - west of 30°W	35.25	-35.58	43.07	-30
PTRA08_UTM_Zone_26N	5015	Portugal - Azores 30°W to 24°W	33.52	-30	42.96	-24
PTRA08_UTM_Zone_28N	5016	Portugal - Madeira and EEZ E of 18°W	29.24	-18	36.46	-12.48
Puerto_Rico_StatePlane_Puerto_Rico_ FIPS_5201	3991	Puerto Rico - onshore	17.87	-67.97	18.57	-65.19
Puerto_Rico_StatePlane_Virgin_Islands_ St_Croix_FIPS_5202	3992	Virgin Islands, US - onshore	17.62	-65.09	18.44	-64.51
Puerto_Rico_UTM_Zone_20N	3920	Virgin Islands, British - onshore	18.28	-64.88	18.78	-64.25
Pulkovo_1942_3_Degree_GK_CM_102E	2610	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
Pulkovo_1942_3_Degree_GK_CM_105E	2611	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
Pulkovo_1942_3_Degree_GK_CM_108E	2612	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
Pulkovo_1942_3_Degree_GK_CM_111E	2613	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
Pulkovo_1942_3_Degree_GK_CM_114E	2614	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
Pulkovo_1942_3_Degree_GK_CM_117E	2615	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
Pulkovo_1942_3_Degree_GK_CM_120E	2616	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
Pulkovo_1942_3_Degree_GK_CM_123E	2617	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
Pulkovo_1942_3_Degree_GK_CM_126E	2618	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
Pulkovo_1942_3_Degree_GK_CM_129E	2619	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
Pulkovo_1942_3_Degree_GK_CM_132E	2620	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
Pulkovo_1942_3_Degree_GK_CM_135E	2621	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
Pulkovo_1942_3_Degree_GK_CM_138E	2622	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
Pulkovo_1942_3_Degree_GK_CM_141E	2623	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
Pulkovo_1942_3_Degree_GK_CM_144E	2624	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
Pulkovo_1942_3_Degree_GK_CM_147E	2625	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
Pulkovo_1942_3_Degree_GK_CM_150E	2626	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
Pulkovo_1942_3_Degree_GK_CM_153E	2627	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
Pulkovo_1942_3_Degree_GK_CM_156E	2628	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
Pulkovo_1942_3_Degree_GK_CM_159E	2629	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
Pulkovo_1942_3_Degree_GK_CM_162E	2630	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
Pulkovo_1942_3_Degree_GK_CM_165E	2631	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
Pulkovo_1942_3_Degree_GK_CM_168E	2632	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
Pulkovo_1942_3_Degree_GK_CM_168W	2640	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
Pulkovo_1942_3_Degree_GK_CM_171E	2633	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
Pulkovo_1942_3_Degree_GK_CM_171W	2639	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
Pulkovo_1942_3_Degree_GK_CM_174E	2634	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
Pulkovo_1942_3_Degree_GK_CM_174W	2638	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
Pulkovo_1942_3_Degree_GK_CM_177E	2635	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
Pulkovo_1942_3_Degree_GK_CM_177W	2637	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
Pulkovo_1942_3_Degree_GK_CM_180E	2636	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
Pulkovo_1942_3_Degree_GK_CM_18E	3147	Russia - west of 19.5°E	54.32	19.2	55.3	19.5
Pulkovo_1942_3_Degree_GK_CM_21E	2582	Europe - FSU - 19.5°E to 22.5°E onshore	48.24	19.57	59.1	22.5
Pulkovo_1942_3_Degree_GK_CM_24E	2583	Europe - FSU - 22.5°E to 25.5°E onshore	47.71	22.5	59.75	25.5
Pulkovo_1942_3_Degree_GK_CM_27E	2584	Europe - FSU - 25.5°E to 28.5°E onshore	45.26	25.49	68.93	28.51
Pulkovo_1942_3_Degree_GK_CM_30E	2585	Europe - FSU - 28.5°E to 31.5°E onshore	45.18	28.5	69.85	31.5
Pulkovo_1942_3_Degree_GK_CM_33E	2586	Europe - FSU - 31.5°E to 34.5°E onshore	44.32	31.5	70.02	34.5
Pulkovo_1942_3_Degree_GK_CM_36E	2587	Europe - FSU - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.5
Pulkovo_1942_3_Degree_GK_CM_39E	2588	Europe - FSU - 37.5°E to 40.5°E onshore	43.07	37.5	68.8	40.5
Pulkovo_1942_3_Degree_GK_CM_42E	2589	Europe - FSU - 40.5°E to 43.5°E onshore	41.01	40.5	68.74	43.51
Pulkovo_1942_3_Degree_GK_CM_45E	2590	Europe - FSU - 43.5°E to 46.5°E onshore	38.84	43.5	80.8	46.5
Pulkovo_1942_3_Degree_GK_CM_48E	2591	Europe - FSU - 46.5°E to 49.5°E onshore	38.31	46.5	80.91	49.5
Pulkovo_1942_3_Degree_GK_CM_51E	2592	Asia - FSU - 49.5°E to 52.5°E onshore	37.66	49.5	81.22	52.5
Pulkovo_1942_3_Degree_GK_CM_54E	2593	Asia - FSU - 52.5°E to 55.5°E onshore	37.33	52.5	81.41	55.5
Pulkovo_1942_3_Degree_GK_CM_57E	2594	Asia - FSU - 55.5°E to 58.5°E onshore	37.64	55.5	81.89	58.5
Pulkovo_1942_3_Degree_GK_CM_60E	2595	Asia - FSU - 58.5°E to 61.5°E onshore	35.51	58.5	81.91	61.5
Pulkovo_1942_3_Degree_GK_CM_63E	2596	Asia - FSU - 61.5°E to 64.5°E onshore	35.14	61.5	81.77	64.5
Pulkovo_1942_3_Degree_GK_CM_66E	2597	Asia - FSU - 64.5°E to 67.5°E onshore	36.27	64.5	81.25	67.5
Pulkovo_1942_3_Degree_GK_CM_69E	2598	Asia - FSU - 67.5°E to 70.5°E onshore	36.93	67.5	77.07	70.5
Pulkovo_1942_3_Degree_GK_CM_72E	2599	Asia - FSU - 70.5°E to 73.5°E onshore	36.67	70.5	73.57	73.5
Pulkovo_1942_3_Degree_GK_CM_75E	2601	Asia - FSU - 73.5°E to 76.5°E onshore	37.22	73.5	79.71	76.5
Pulkovo_1942_3_Degree_GK_CM_78E	2602	Asia - FSU - 76.5°E to 79.5°E onshore	40.44	76.5	81.03	79.5
Pulkovo_1942_3_Degree_GK_CM_81E	2603	Asia - FSU - 79.5°E to 82.5°E onshore	41.82	79.5	81.03	82.5
Pulkovo_1942_3_Degree_GK_CM_84E	2604	Asia - FSU - 82.5°E to 85.5°E onshore	45.11	82.5	77.56	85.5
Pulkovo_1942_3_Degree_GK_CM_87E	2605	Asia - FSU - 85.5°E to 88.5°E onshore	47.05	85.5	77.16	88.5
Pulkovo_1942_3_Degree_GK_CM_90E	2606	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
Pulkovo_1942_3_Degree_GK_CM_93E	2607	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
Pulkovo_1942_3_Degree_GK_CM_96E	2608	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
Pulkovo_1942_3_Degree_GK_CM_99E	2609	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
Pulkovo_1942_3_Degree_GK_Zone_10	2526	Europe - FSU - 28.5°E to 31.5°E onshore	45.18	28.5	69.85	31.5
Pulkovo_1942_3_Degree_GK_Zone_11	2527	Europe - FSU - 31.5°E to 34.5°E onshore	44.32	31.5	70.02	34.5
Pulkovo_1942_3_Degree_GK_Zone_12	2528	Europe - FSU - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.5
Pulkovo_1942_3_Degree_GK_Zone_13	2529	Europe - FSU - 37.5°E to 40.5°E onshore	43.07	37.5	68.8	40.5
Pulkovo_1942_3_Degree_GK_Zone_14	2530	Europe - FSU - 40.5°E to 43.5°E onshore	41.01	40.5	68.74	43.51
Pulkovo_1942_3_Degree_GK_Zone_15	2531	Europe - FSU - 43.5°E to 46.5°E onshore	38.84	43.5	80.8	46.5
Pulkovo_1942_3_Degree_GK_Zone_16	2532	Europe - FSU - 46.5°E to 49.5°E onshore	38.31	46.5	80.91	49.5
Pulkovo_1942_3_Degree_GK_Zone_17	2533	Asia - FSU - 49.5°E to 52.5°E onshore	37.66	49.5	81.22	52.5
Pulkovo_1942_3_Degree_GK_Zone_18	2534	Asia - FSU - 52.5°E to 55.5°E onshore	37.33	52.5	81.41	55.5
Pulkovo_1942_3_Degree_GK_Zone_19	2535	Asia - FSU - 55.5°E to 58.5°E onshore	37.64	55.5	81.89	58.5
Pulkovo_1942_3_Degree_GK_Zone_20	2536	Asia - FSU - 58.5°E to 61.5°E onshore	35.51	58.5	81.91	61.5
Pulkovo_1942_3_Degree_GK_Zone_21	2537	Asia - FSU - 61.5°E to 64.5°E onshore	35.14	61.5	81.77	64.5
Pulkovo_1942_3_Degree_GK_Zone_22	2538	Asia - FSU - 64.5°E to 67.5°E onshore	36.27	64.5	81.25	67.5
Pulkovo_1942_3_Degree_GK_Zone_23	2539	Asia - FSU - 67.5°E to 70.5°E onshore	36.93	67.5	77.07	70.5
Pulkovo_1942_3_Degree_GK_Zone_24	2540	Asia - FSU - 70.5°E to 73.5°E onshore	36.67	70.5	73.57	73.5
Pulkovo_1942_3_Degree_GK_Zone_25	2541	Asia - FSU - 73.5°E to 76.5°E onshore	37.22	73.5	79.71	76.5
Pulkovo_1942_3_Degree_GK_Zone_26	2542	Asia - FSU - 76.5°E to 79.5°E onshore	40.44	76.5	81.03	79.5
Pulkovo_1942_3_Degree_GK_Zone_27	2543	Asia - FSU - 79.5°E to 82.5°E onshore	41.82	79.5	81.03	82.5
Pulkovo_1942_3_Degree_GK_Zone_28	2544	Asia - FSU - 82.5°E to 85.5°E onshore	45.11	82.5	77.56	85.5
Pulkovo_1942_3_Degree_GK_Zone_29	2545	Asia - FSU - 85.5°E to 88.5°E onshore	47.05	85.5	77.16	88.5
Pulkovo_1942_3_Degree_GK_Zone_30	2546	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
Pulkovo_1942_3_Degree_GK_Zone_31	2547	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
Pulkovo_1942_3_Degree_GK_Zone_32	2548	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
Pulkovo_1942_3_Degree_GK_Zone_33	2549	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
Pulkovo_1942_3_Degree_GK_Zone_34	2551	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
Pulkovo_1942_3_Degree_GK_Zone_35	2552	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
Pulkovo_1942_3_Degree_GK_Zone_36	2553	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
Pulkovo_1942_3_Degree_GK_Zone_37	2554	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
Pulkovo_1942_3_Degree_GK_Zone_38	2555	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
Pulkovo_1942_3_Degree_GK_Zone_39	2556	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
Pulkovo_1942_3_Degree_GK_Zone_40	2557	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
Pulkovo_1942_3_Degree_GK_Zone_41	2558	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
Pulkovo_1942_3_Degree_GK_Zone_42	2559	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
Pulkovo_1942_3_Degree_GK_Zone_43	2560	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
Pulkovo_1942_3_Degree_GK_Zone_44	2561	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
Pulkovo_1942_3_Degree_GK_Zone_45	2562	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
Pulkovo_1942_3_Degree_GK_Zone_46	2563	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
Pulkovo_1942_3_Degree_GK_Zone_47	2564	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
Pulkovo_1942_3_Degree_GK_Zone_48	2565	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
Pulkovo_1942_3_Degree_GK_Zone_49	2566	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
Pulkovo_1942_3_Degree_GK_Zone_50	2567	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
Pulkovo_1942_3_Degree_GK_Zone_51	2568	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
Pulkovo_1942_3_Degree_GK_Zone_52	2569	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
Pulkovo_1942_3_Degree_GK_Zone_53	2570	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
Pulkovo_1942_3_Degree_GK_Zone_54	2571	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
Pulkovo_1942_3_Degree_GK_Zone_55	2572	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
Pulkovo_1942_3_Degree_GK_Zone_56	2573	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
Pulkovo_1942_3_Degree_GK_Zone_57	2574	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
Pulkovo_1942_3_Degree_GK_Zone_58	2575	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
Pulkovo_1942_3_Degree_GK_Zone_59	2576	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
Pulkovo_1942_3_Degree_GK_Zone_6	3146	Russia - west of 19.5°E	54.32	19.2	55.3	19.5
Pulkovo_1942_3_Degree_GK_Zone_60	3389	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
Pulkovo_1942_3_Degree_GK_Zone_61	2578	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
Pulkovo_1942_3_Degree_GK_Zone_62	2579	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
Pulkovo_1942_3_Degree_GK_Zone_63	2580	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
Pulkovo_1942_3_Degree_GK_Zone_64	2581	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
Pulkovo_1942_3_Degree_GK_Zone_7	2523	Europe - FSU - 19.5°E to 22.5°E onshore	48.24	19.57	59.1	22.5
Pulkovo_1942_3_Degree_GK_Zone_8	2524	Europe - FSU - 22.5°E to 25.5°E onshore	47.71	22.5	59.75	25.5
Pulkovo_1942_3_Degree_GK_Zone_9	2525	Europe - FSU - 25.5°E to 28.5°E onshore	45.26	25.49	68.93	28.51
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_10	3840	Europe - 28.5°E to 31.5°E onshore and S- 42(58) by country	43.34	28.5	45.44	29.74
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_3	3837	Germany - East Germany - west of 10.5°E	50.35	9.92	51.56	10.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_3_E-N	5670	Germany - East Germany - west of 10.5°E	50.35	9.92	51.56	10.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_4	3838	Europe - 10.5°E to 13.5°E onshore by country	48.97	10.5	54.74	13.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_4_E-N	5671	Europe - 10.5°E to 13.5°E onshore by country	48.97	10.5	54.74	13.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_5	3329	Europe - 13.5°E to 16.5°E onshore and S- 42(58) by country	46.54	13.5	54.72	16.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_5_E-N	5672	Europe - 13.5°E to 16.5°E onshore and S- 42(58) by country	46.54	13.5	54.72	16.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_6	3330	Europe - 16.5°E to 19.5°E onshore and S- 42(58) by country	40.14	16.5	54.89	19.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_7	3331	Europe - 19.5°E to 22.5°E onshore and S- 42(58) by country	39.64	19.5	54.51	22.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_8	3332	Europe - 22.5°E to 25.5°E onshore and S- 42(58) by country	41.24	22.5	54.41	25.5
Pulkovo_1942_Adj_1958_3_Degree_GK_ Zone_9	3839	Europe - 25.5°E to 28.5°E onshore and S- 42(58) by country	41.28	25.5	48.27	28.5
Pulkovo_1942_Adj_1958_GK_Zone_2	3833	Germany - East Germany - west of 12°E	50.2	9.92	54.23	12
Pulkovo_1942_Adj_1958_GK_Zone_2_ E-N	5631	Germany - East Germany - west of 12°E	50.2	9.92	54.23	12
Pulkovo_1942_Adj_1958_GK_Zone_3	3333	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1942_Adj_1958_GK_Zone_3_ E-N	5663	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1942_Adj_1958_GK_Zone_4	3334	Europe - 18°E to 24°E onshore and S-42(58) by country	39.64	18	54.89	24
Pulkovo_1942_Adj_1958_GK_Zone_5	3335	Europe - 24°E to 30°E onshore and S-42(58) by country	41.24	24	50.93	29.74
Pulkovo_1942_Adj_1958_GUGiK-80	3328	Poland - onshore	49	14.14	54.89	24.15
Pulkovo_1942_Adj_1958_Poland_Zone_I	3120	Poland - zone I	49	18	52.34	24.15
Pulkovo_1942_Adj_1958_Poland_Zone_II	2172	Poland - zone II	51.33	19	54.51	23.95
Pulkovo_1942_Adj_1958_Poland_Zone_ III	2173	Poland - zone III	52.16	14.14	54.89	20
Pulkovo_1942_Adj_1958_Poland_Zone_ IV	2174	Poland - zone IV	49.39	14.14	53.34	19.09
Pulkovo_1942_Adj_1958_Poland_Zone_V	2175	Poland - zone V	49.39	18.33	51.34	19.67
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_3	2397	Germany - East Germany - west of 10.5°E	50.35	9.92	51.56	10.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_3_E-N	5673	Germany - East Germany - west of 10.5°E	50.35	9.92	51.56	10.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_4	2398	Europe - 10.5°E to 13.5°E onshore by country	48.97	10.5	54.74	13.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_4_E-N	5674	Europe - 10.5°E to 13.5°E onshore by country	48.97	10.5	54.74	13.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_5	2399	Europe - 13.5°E to 16.5°E onshore and S- 42(83) by country	46.54	13.5	54.72	16.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_5_E-N	5675	Europe - 13.5°E to 16.5°E onshore and S- 42(83) by country	46.54	13.5	54.72	16.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_6	3841	Europe - 16.5°E to 19.5°E onshore and S- 42(83) by country	45.74	16.5	50.45	19.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_7	4417	Europe - 19.5°E to 22.5°E onshore and S- 42(83) by country	46.1	19.5	49.59	22.5
Pulkovo_1942_Adj_1983_3_Degree_GK_ Zone_8	4434	Europe - 22.5°E to 25.5°E onshore and S- 42(83) by country	47.76	22.5	49.1	22.9
Pulkovo_1942_Adj_1983_GK_Zone_2	3834	Germany - East Germany - west of 12°E	50.2	9.92	54.23	12
Pulkovo_1942_Adj_1983_GK_Zone_2_ E-N	5664	Germany - East Germany - west of 12°E	50.2	9.92	54.23	12
Pulkovo_1942_Adj_1983_GK_Zone_3	3835	Europe - 12°E to 18°E onshore and S-42(83) by country	45.78	12	54.74	18.01
Pulkovo_1942_Adj_1983_GK_Zone_3_E- N	5665	Europe - 12°E to 18°E onshore and S-42(83) by country	45.78	12	54.74	18.01
Pulkovo_1942_Adj_1983_GK_Zone_4	3836	Europe - 18°E to 24°E onshore and S-42(83) by country	45.74	18	50.06	22.9
Pulkovo_1942_Adj_58_Stereo_70	3844	Romania	43.44	20.26	48.27	31.41
Pulkovo_1942_Caspian_Sea_Mercator	3388	Asia - FSU - Caspian Sea	37.35	46.95	46.97	53.93
Pulkovo_1942_CS63_Zone_A1	2935	Asia - FSU - CS63 zone A1	41.37	39.99	43.59	43.04
Pulkovo_1942_CS63_Zone_A2	2936	Asia - FSU - CS63 zone A2	38.87	43.03	43.05	46.04
Pulkovo_1942_CS63_Zone_A3	2937	Asia - FSU - CS63 zone A3	38.38	46.03	42.1	49.04
Pulkovo_1942_CS63_Zone_A4	2938	Asia - FSU - CS63 zone A4	37.89	49.03	42.59	51.73
Pulkovo_1942_CS63_Zone_C0	3350	Europe - FSU - CS63 zone C0	54.17	19.57	59.27	23.45
Pulkovo_1942_CS63_Zone_C1	3351	Europe - FSU - CS63 zone C1	53.89	23.45	59.72	26.45
Pulkovo_1942_CS63_Zone_C2	3352	Europe - FSU - CS63 zone C2	55.15	26.45	59.61	28.24
Pulkovo_1942_CS63_Zone_K2	2939	Asia - FSU - CS63 zone K2	41.15	49.26	51.77	52.27
Pulkovo_1942_CS63_Zone_K3	2940	Asia - FSU - CS63 zone K3	41.46	52.26	51.79	55.27
Pulkovo_1942_CS63_Zone_K4	2941	Asia - FSU - CS63 zone K4	41.26	55.26	51.14	58.27
Pulkovo_1942_CS63_zone_X1	7825	Ukraine - west of 25°E	47.71	22.15	51.92	25.01
Pulkovo_1942_CS63_zone_X2	7826	Ukraine - 25°E to 28°E	47.72	25	51.96	28.01
Pulkovo_1942_CS63_zone_X3	7827	Ukraine - 28°E to 31°E onshore	45.18	28	52.09	31.01
Pulkovo_1942_CS63_zone_X4	7828	Ukraine - 31°E to 34°E onshore	44.32	31	52.38	34.01
Pulkovo_1942_CS63_zone_X5	7829	Ukraine - 34°E to 37°E onshore	44.33	34	52.25	37.01
Pulkovo_1942_CS63_zone_X6	7830	Ukraine - 37°E to 40°E onshore	46.8	37	50.44	40.01
Pulkovo_1942_CS63_zone_X7	7831	Ukraine - east of 40°E	48.8	40	49.62	40.18
Pulkovo_1942_Gauss-Kruger_CM_105E	2508	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1942_Gauss-Kruger_CM_111E	2509	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1942_Gauss-Kruger_CM_117E	2510	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1942_Gauss-Kruger_CM_123E	2511	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1942_Gauss-Kruger_CM_129E	2512	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1942_Gauss-Kruger_CM_135E	2513	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1942_Gauss-Kruger_CM_141E	2514	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1942_Gauss-Kruger_CM_147E	2515	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1942_Gauss-Kruger_CM_153E	2516	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1942_Gauss-Kruger_CM_159E	2517	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1942_Gauss-Kruger_CM_165E	2518	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1942_Gauss-Kruger_CM_171E	2519	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1942_Gauss-Kruger_CM_171W	2522	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1942_Gauss-Kruger_CM_177E	2520	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1942_Gauss-Kruger_CM_177W	2521	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1942_Gauss-Kruger_CM_21E	2494	Europe - FSU onshore 18°E to 24°E and S-42 by country	47.95	19.57	59.44	24
Pulkovo_1942_Gauss-Kruger_CM_27E	2495	Europe - FSU onshore 24°E to 30°E and S-42 by country	45.18	24	69.47	30.01
Pulkovo_1942_Gauss-Kruger_CM_33E	2496	Europe - FSU onshore 30°E to 36°E	44.32	30	70.02	36
Pulkovo_1942_Gauss-Kruger_CM_39E	2497	Europe - FSU onshore 36°E to 42°E	41.43	36	69.23	42
Pulkovo_1942_Gauss-Kruger_CM_45E	2498	Europe - FSU onshore 42°E to 48°E	38.84	42	80.91	48.01
Pulkovo_1942_Gauss-Kruger_CM_51E	2499	Asia - FSU onshore 48°E to 54°E	37.34	48	81.4	54
Pulkovo_1942_Gauss-Kruger_CM_57E	2500	Asia - FSU onshore 54°E to 60°E	37.05	54	81.91	60
Pulkovo_1942_Gauss-Kruger_CM_63E	2501	Asia - FSU onshore 60°E to 66°E	35.14	60	81.77	66
Pulkovo_1942_Gauss-Kruger_CM_69E	2502	Asia - FSU onshore 66°E to 72°E	36.67	66	77.07	72
Pulkovo_1942_Gauss-Kruger_CM_75E	2503	Asia - FSU onshore 72°E to 78°E	36.79	72	79.71	78
Pulkovo_1942_Gauss-Kruger_CM_81E	2504	Asia - FSU onshore 78°E to 84°E	41.04	78	81.03	84.01
Pulkovo_1942_Gauss-Kruger_CM_87E	2505	Asia - FSU onshore 84°E to 90°E	46.82	84	81.27	90
Pulkovo_1942_Gauss-Kruger_CM_93E	2506	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1942_Gauss-Kruger_CM_99E	2507	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1942_GK_Zone_10	28410	Asia - FSU onshore 54°E to 60°E	37.05	54	81.91	60
Pulkovo_1942_GK_Zone_10N	28470	Asia - FSU onshore 54°E to 60°E	37.05	54	81.91	60
Pulkovo_1942_GK_Zone_11	28411	Asia - FSU onshore 60°E to 66°E	35.14	60	81.77	66
Pulkovo_1942_GK_Zone_11N	28471	Asia - FSU onshore 60°E to 66°E	35.14	60	81.77	66
Pulkovo_1942_GK_Zone_12	28412	Asia - FSU onshore 66°E to 72°E	36.67	66	77.07	72
Pulkovo_1942_GK_Zone_12N	28472	Asia - FSU onshore 66°E to 72°E	36.67	66	77.07	72
Pulkovo_1942_GK_Zone_13	28413	Asia - FSU onshore 72°E to 78°E	36.79	72	79.71	78
Pulkovo_1942_GK_Zone_13N	28473	Asia - FSU onshore 72°E to 78°E	36.79	72	79.71	78
Pulkovo_1942_GK_Zone_14	28414	Asia - FSU onshore 78°E to 84°E	41.04	78	81.03	84.01
Pulkovo_1942_GK_Zone_14N	28474	Asia - FSU onshore 78°E to 84°E	41.04	78	81.03	84.01
Pulkovo_1942_GK_Zone_15	28415	Asia - FSU onshore 84°E to 90°E	46.82	84	81.27	90
Pulkovo_1942_GK_Zone_15N	28475	Asia - FSU onshore 84°E to 90°E	46.82	84	81.27	90
Pulkovo_1942_GK_Zone_16	28416	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1942_GK_Zone_16N	28476	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1942_GK_Zone_17	28417	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1942_GK_Zone_17N	28477	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1942_GK_Zone_18	28418	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1942_GK_Zone_18N	28478	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1942_GK_Zone_19	28419	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1942_GK_Zone_19N	28479	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1942_GK_Zone_2	28402	Europe - 6°E to 12°E and Pulkovo by country	50.21	9.93	54.18	12
Pulkovo_1942_GK_Zone_20	28420	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1942_GK_Zone_20N	28480	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1942_GK_Zone_21	28421	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1942_GK_Zone_21N	28481	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1942_GK_Zone_22	28422	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1942_GK_Zone_22N	28482	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1942_GK_Zone_23	28423	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1942_GK_Zone_23N	28483	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1942_GK_Zone_24	28424	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1942_GK_Zone_24N	28484	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1942_GK_Zone_25	28425	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1942_GK_Zone_25N	28485	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1942_GK_Zone_26	28426	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1942_GK_Zone_26N	28486	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1942_GK_Zone_27	28427	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1942_GK_Zone_27N	28487	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1942_GK_Zone_28	28428	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1942_GK_Zone_28N	28488	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1942_GK_Zone_29	28429	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1942_GK_Zone_29N	28489	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1942_GK_Zone_2N	28462	Europe - 6°E to 12°E and Pulkovo by country	50.21	9.93	54.18	12
Pulkovo_1942_GK_Zone_3	28403	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1942_GK_Zone_30	28430	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1942_GK_Zone_30N	28490	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1942_GK_Zone_31	28431	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1942_GK_Zone_31N	28491	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1942_GK_Zone_32	28432	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1942_GK_Zone_32N	28492	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1942_GK_Zone_3N	28463	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1942_GK_Zone_4	28404	Europe - FSU onshore 18°E to 24°E and S-42 by country	47.95	19.57	59.44	24
Pulkovo_1942_GK_Zone_4N	28464	Europe - FSU onshore 18°E to 24°E and S-42 by country	47.95	19.57	59.44	24
Pulkovo_1942_GK_Zone_5	28405	Europe - FSU onshore 24°E to 30°E and S-42 by country	45.18	24	69.47	30.01
Pulkovo_1942_GK_Zone_5N	28465	Europe - FSU onshore 24°E to 30°E and S-42 by country	45.18	24	69.47	30.01
Pulkovo_1942_GK_Zone_6	28406	Europe - FSU onshore 30°E to 36°E	44.32	30	70.02	36
Pulkovo_1942_GK_Zone_6N	28466	Europe - FSU onshore 30°E to 36°E	44.32	30	70.02	36
Pulkovo_1942_GK_Zone_7	28407	Europe - FSU onshore 36°E to 42°E	41.43	36	69.23	42
Pulkovo_1942_GK_Zone_7N	28467	Europe - FSU onshore 36°E to 42°E	41.43	36	69.23	42
Pulkovo_1942_GK_Zone_8	28408	Europe - FSU onshore 42°E to 48°E	38.84	42	80.91	48.01
Pulkovo_1942_GK_Zone_8N	28468	Europe - FSU onshore 42°E to 48°E	38.84	42	80.91	48.01
Pulkovo_1942_GK_Zone_9	28409	Asia - FSU onshore 48°E to 54°E	37.34	48	81.4	54
Pulkovo_1942_GK_Zone_9N	28469	Asia - FSU onshore 48°E to 54°E	37.34	48	81.4	54
Pulkovo_1995_3_Degree_GK_CM_102E	2726	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
Pulkovo_1995_3_Degree_GK_CM_105E	2727	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
Pulkovo_1995_3_Degree_GK_CM_108E	2728	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
Pulkovo_1995_3_Degree_GK_CM_111E	2729	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
Pulkovo_1995_3_Degree_GK_CM_114E	2730	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
Pulkovo_1995_3_Degree_GK_CM_117E	2731	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
Pulkovo_1995_3_Degree_GK_CM_120E	2732	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
Pulkovo_1995_3_Degree_GK_CM_123E	2733	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
Pulkovo_1995_3_Degree_GK_CM_126E	2734	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
Pulkovo_1995_3_Degree_GK_CM_129E	2735	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
Pulkovo_1995_3_Degree_GK_CM_132E	2738	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
Pulkovo_1995_3_Degree_GK_CM_135E	2739	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
Pulkovo_1995_3_Degree_GK_CM_138E	2740	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
Pulkovo_1995_3_Degree_GK_CM_141E	2741	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
Pulkovo_1995_3_Degree_GK_CM_144E	2742	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
Pulkovo_1995_3_Degree_GK_CM_147E	2743	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
Pulkovo_1995_3_Degree_GK_CM_150E	2744	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
Pulkovo_1995_3_Degree_GK_CM_153E	2745	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
Pulkovo_1995_3_Degree_GK_CM_156E	2746	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
Pulkovo_1995_3_Degree_GK_CM_159E	2747	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
Pulkovo_1995_3_Degree_GK_CM_162E	2748	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
Pulkovo_1995_3_Degree_GK_CM_165E	2749	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
Pulkovo_1995_3_Degree_GK_CM_168E	2750	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
Pulkovo_1995_3_Degree_GK_CM_168W	2758	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
Pulkovo_1995_3_Degree_GK_CM_171E	2751	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
Pulkovo_1995_3_Degree_GK_CM_171W	2757	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
Pulkovo_1995_3_Degree_GK_CM_174E	2752	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
Pulkovo_1995_3_Degree_GK_CM_174W	2756	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
Pulkovo_1995_3_Degree_GK_CM_177E	2753	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
Pulkovo_1995_3_Degree_GK_CM_177W	2755	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
Pulkovo_1995_3_Degree_GK_CM_180E	2754	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
Pulkovo_1995_3_Degree_GK_CM_18E	3151	Russia - west of 19.5°E	54.32	19.2	55.3	19.5
Pulkovo_1995_3_Degree_GK_CM_21E	2699	Russia - 19.5°E to 22.5°E onshore	54.32	19.57	55.32	22.5
Pulkovo_1995_3_Degree_GK_CM_24E	2700	Russia - 22.5°E to 25.5°E onshore	54.34	22.5	55.07	22.87
Pulkovo_1995_3_Degree_GK_CM_27E	2701	Russia - 25.5°E to 28.5°E onshore	56.05	26.61	68.93	28.51
Pulkovo_1995_3_Degree_GK_CM_30E	2702	Russia - 28.5°E to 31.5°E onshore	52.85	28.5	69.85	31.5
Pulkovo_1995_3_Degree_GK_CM_33E	2703	Russia - 31.5°E to 34.5°E onshore	51.24	31.5	70.02	34.5
Pulkovo_1995_3_Degree_GK_CM_36E	2704	Russia - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.51
Pulkovo_1995_3_Degree_GK_CM_39E	2705	Russia - 37.5°E to 40.5°E onshore	43.33	37.5	68.8	40.5
Pulkovo_1995_3_Degree_GK_CM_42E	2706	Russia - 40.5°E to 43.5°E onshore	42.87	40.5	68.74	43.5
Pulkovo_1995_3_Degree_GK_CM_45E	2707	Russia - 43.5°E to 46.5°E onshore	41.89	43.5	80.8	46.5
Pulkovo_1995_3_Degree_GK_CM_48E	2708	Russia - 46.5°E to 49.5°E onshore	41.19	46.5	80.91	49.5
Pulkovo_1995_3_Degree_GK_CM_51E	2709	Russia - 49.5°E to 52.5°E onshore	42.36	49.5	81.22	52.5
Pulkovo_1995_3_Degree_GK_CM_54E	2710	Russia - 52.5°E to 55.5°E onshore	50.52	52.5	81.41	55.5
Pulkovo_1995_3_Degree_GK_CM_57E	2711	Russia - 55.5°E to 58.5°E onshore	50.53	55.5	81.89	58.5
Pulkovo_1995_3_Degree_GK_CM_60E	2712	Russia - 58.5°E to 61.5°E onshore	50.47	58.5	81.91	61.5
Pulkovo_1995_3_Degree_GK_CM_63E	2713	Russia - 61.5°E to 64.5°E onshore	51.03	61.5	81.77	64.5
Pulkovo_1995_3_Degree_GK_CM_66E	2714	Russia - 64.5°E to 67.5°E onshore	54.31	64.5	81.25	67.5
Pulkovo_1995_3_Degree_GK_CM_69E	2715	Russia - 67.5°E to 70.5°E onshore	54.85	67.5	77.07	70.5
Pulkovo_1995_3_Degree_GK_CM_72E	2716	Russia - 70.5°E to 73.5°E onshore	53.43	70.5	73.57	73.5
Pulkovo_1995_3_Degree_GK_CM_75E	2717	Russia - 73.5°E to 76.5°E onshore	53.47	73.5	79.71	76.5
Pulkovo_1995_3_Degree_GK_CM_78E	2718	Russia - 76.5°E to 79.5°E onshore	51.49	76.5	81.03	79.5
Pulkovo_1995_3_Degree_GK_CM_81E	2719	Russia - 79.5°E to 82.5°E onshore	50.7	79.5	81.03	82.5
Pulkovo_1995_3_Degree_GK_CM_84E	2720	Russia - 82.5°E to 85.5°E onshore	49.58	82.5	77.56	85.5
Pulkovo_1995_3_Degree_GK_CM_87E	2721	Russia - 85.5°E to 88.5°E onshore	49.07	85.5	77.16	88.5
Pulkovo_1995_3_Degree_GK_CM_90E	2722	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
Pulkovo_1995_3_Degree_GK_CM_93E	2723	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
Pulkovo_1995_3_Degree_GK_CM_96E	2724	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
Pulkovo_1995_3_Degree_GK_CM_99E	2725	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
Pulkovo_1995_3_Degree_GK_Zone_10	2644	Russia - 28.5°E to 31.5°E onshore	52.85	28.5	69.85	31.5
Pulkovo_1995_3_Degree_GK_Zone_11	2645	Russia - 31.5°E to 34.5°E onshore	51.24	31.5	70.02	34.5
Pulkovo_1995_3_Degree_GK_Zone_12	2646	Russia - 34.5°E to 37.5°E onshore	44.61	34.5	69.39	37.51
Pulkovo_1995_3_Degree_GK_Zone_13	2647	Russia - 37.5°E to 40.5°E onshore	43.33	37.5	68.8	40.5
Pulkovo_1995_3_Degree_GK_Zone_14	2648	Russia - 40.5°E to 43.5°E onshore	42.87	40.5	68.74	43.5
Pulkovo_1995_3_Degree_GK_Zone_15	2649	Russia - 43.5°E to 46.5°E onshore	41.89	43.5	80.8	46.5
Pulkovo_1995_3_Degree_GK_Zone_16	2650	Russia - 46.5°E to 49.5°E onshore	41.19	46.5	80.91	49.5
Pulkovo_1995_3_Degree_GK_Zone_17	2651	Russia - 49.5°E to 52.5°E onshore	42.36	49.5	81.22	52.5
Pulkovo_1995_3_Degree_GK_Zone_18	2652	Russia - 52.5°E to 55.5°E onshore	50.52	52.5	81.41	55.5
Pulkovo_1995_3_Degree_GK_Zone_19	2653	Russia - 55.5°E to 58.5°E onshore	50.53	55.5	81.89	58.5
Pulkovo_1995_3_Degree_GK_Zone_20	2654	Russia - 58.5°E to 61.5°E onshore	50.47	58.5	81.91	61.5
Pulkovo_1995_3_Degree_GK_Zone_21	2655	Russia - 61.5°E to 64.5°E onshore	51.03	61.5	81.77	64.5
Pulkovo_1995_3_Degree_GK_Zone_22	2656	Russia - 64.5°E to 67.5°E onshore	54.31	64.5	81.25	67.5
Pulkovo_1995_3_Degree_GK_Zone_23	2657	Russia - 67.5°E to 70.5°E onshore	54.85	67.5	77.07	70.5
Pulkovo_1995_3_Degree_GK_Zone_24	2658	Russia - 70.5°E to 73.5°E onshore	53.43	70.5	73.57	73.5
Pulkovo_1995_3_Degree_GK_Zone_25	2659	Russia - 73.5°E to 76.5°E onshore	53.47	73.5	79.71	76.5
Pulkovo_1995_3_Degree_GK_Zone_26	2660	Russia - 76.5°E to 79.5°E onshore	51.49	76.5	81.03	79.5
Pulkovo_1995_3_Degree_GK_Zone_27	2661	Russia - 79.5°E to 82.5°E onshore	50.7	79.5	81.03	82.5
Pulkovo_1995_3_Degree_GK_Zone_28	2662	Russia - 82.5°E to 85.5°E onshore	49.58	82.5	77.56	85.5
Pulkovo_1995_3_Degree_GK_Zone_29	2663	Russia - 85.5°E to 88.5°E onshore	49.07	85.5	77.16	88.5
Pulkovo_1995_3_Degree_GK_Zone_30	2664	Russia - 88.5°E to 91.5°E onshore	49.44	88.5	81.28	91.5
Pulkovo_1995_3_Degree_GK_Zone_31	2665	Russia - 91.5°E to 94.5°E onshore	50.16	91.5	81.26	94.5
Pulkovo_1995_3_Degree_GK_Zone_32	2666	Russia - 94.5°E to 97.5°E onshore	49.73	94.5	81.35	97.5
Pulkovo_1995_3_Degree_GK_Zone_33	2667	Russia - 97.5°E to 100.5°E onshore	49.79	97.5	80.9	100.5
Pulkovo_1995_3_Degree_GK_Zone_34	2668	Russia - 100.5°E to 103.5°E onshore	50.17	100.5	79.71	103.5
Pulkovo_1995_3_Degree_GK_Zone_35	2669	Russia - 103.5°E to 106.5°E onshore	50.13	103.5	79.21	106.5
Pulkovo_1995_3_Degree_GK_Zone_36	2670	Russia - 106.5°E to 109.5°E onshore	49.25	106.5	78.4	109.5
Pulkovo_1995_3_Degree_GK_Zone_37	2671	Russia - 109.5°E to 112.5°E onshore	49.14	109.5	76.81	112.5
Pulkovo_1995_3_Degree_GK_Zone_38	2672	Russia - 112.5°E to 115.5°E onshore	49.49	112.5	76.7	115.5
Pulkovo_1995_3_Degree_GK_Zone_39	2673	Russia - 115.5°E to 118.5°E onshore	49.51	115.5	74.43	118.5
Pulkovo_1995_3_Degree_GK_Zone_40	2674	Russia - 118.5°E to 121.5°E onshore	49.87	118.5	73.63	121.5
Pulkovo_1995_3_Degree_GK_Zone_41	2675	Russia - 121.5°E to 124.5°E onshore	53.18	121.5	74	124.5
Pulkovo_1995_3_Degree_GK_Zone_42	2676	Russia - 124.5°E to 127.5°E onshore	49.88	124.5	74	127.5
Pulkovo_1995_3_Degree_GK_Zone_43	2677	Russia - 127.5°E to 130.5°E onshore	42.67	127.5	73.59	130.5
Pulkovo_1995_3_Degree_GK_Zone_44	2678	Russia - 130.5°E to 133.5°E onshore	42.25	130.5	71.99	133.5
Pulkovo_1995_3_Degree_GK_Zone_45	2679	Russia - 133.5°E to 136.5°E onshore	42.74	133.5	75.9	136.5
Pulkovo_1995_3_Degree_GK_Zone_46	2680	Russia - 136.5°E to 139.5°E onshore	44.76	136.5	76.27	139.5
Pulkovo_1995_3_Degree_GK_Zone_47	2681	Russia - 139.5°E to 142.5°E onshore	45.84	139.5	76.23	142.5
Pulkovo_1995_3_Degree_GK_Zone_48	2682	Russia - 142.5°E to 145.5°E onshore	43.61	142.5	75.98	145.5
Pulkovo_1995_3_Degree_GK_Zone_49	2683	Russia - 145.5°E to 148.5°E onshore	43.6	145.5	76.76	148.5
Pulkovo_1995_3_Degree_GK_Zone_50	2684	Russia - 148.5°E to 151.5°E onshore	45.21	148.5	76.82	151.5
Pulkovo_1995_3_Degree_GK_Zone_51	2685	Russia - 151.5°E to 154.5°E onshore	46.72	151.5	76.26	154.5
Pulkovo_1995_3_Degree_GK_Zone_52	2686	Russia - 154.5°E to 157.5°E onshore	49.02	154.5	77.2	157.5
Pulkovo_1995_3_Degree_GK_Zone_53	2687	Russia - 157.5°E to 160.5°E onshore	51.36	157.5	71.12	160.5
Pulkovo_1995_3_Degree_GK_Zone_54	2688	Russia - 160.5°E to 163.5°E onshore	54.34	160.5	70.98	163.5
Pulkovo_1995_3_Degree_GK_Zone_55	2689	Russia - 163.5°E to 166.5°E onshore	54.69	163.5	69.82	166.5
Pulkovo_1995_3_Degree_GK_Zone_56	2690	Russia - 166.5°E to 169.5°E onshore	54.45	166.5	70.07	169.5
Pulkovo_1995_3_Degree_GK_Zone_57	2691	Russia - 169.5°E to 172.5°E onshore	59.86	169.5	70.19	172.5
Pulkovo_1995_3_Degree_GK_Zone_58	2692	Russia - 172.5°E to 175.5°E onshore	60.99	172.5	70.02	175.5
Pulkovo_1995_3_Degree_GK_Zone_59	2693	Russia - 175.5°E to 178.5°E onshore	62.09	175.5	71.1	178.5
Pulkovo_1995_3_Degree_GK_Zone_6	3150	Russia - west of 19.5°E	54.32	19.2	55.3	19.5
Pulkovo_1995_3_Degree_GK_Zone_60	3390	Russia - 178.5°E to 178.5°W onshore	62.24	178.5	71.65	-178.5
Pulkovo_1995_3_Degree_GK_Zone_61	2695	Russia - 178.5°W to 175.5°W onshore	64.74	-178.5	71.61	-175.5
Pulkovo_1995_3_Degree_GK_Zone_62	2696	Russia - 175.5°W to 172.5°W onshore	64.2	-175.5	67.78	-172.5
Pulkovo_1995_3_Degree_GK_Zone_63	2697	Russia - 172.5°W to 169.5°W onshore	64.35	-172.5	67.06	-169.57
Pulkovo_1995_3_Degree_GK_Zone_64	2698	Russia - east of 169.5°W onshore	65.7	-169.22	65.86	-168.97
Pulkovo_1995_3_Degree_GK_Zone_7	2641	Russia - 19.5°E to 22.5°E onshore	54.32	19.57	55.32	22.5
Pulkovo_1995_3_Degree_GK_Zone_8	2642	Russia - 22.5°E to 25.5°E onshore	54.34	22.5	55.07	22.87
Pulkovo_1995_3_Degree_GK_Zone_9	2643	Russia - 25.5°E to 28.5°E onshore	56.05	26.61	68.93	28.51
Pulkovo_1995_Gauss-Kruger_CM_105E	2477	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1995_Gauss-Kruger_CM_111E	2478	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1995_Gauss-Kruger_CM_117E	2479	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1995_Gauss-Kruger_CM_123E	2480	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1995_Gauss-Kruger_CM_129E	2481	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1995_Gauss-Kruger_CM_135E	2482	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1995_Gauss-Kruger_CM_141E	2483	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1995_Gauss-Kruger_CM_147E	2484	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1995_Gauss-Kruger_CM_153E	2485	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1995_Gauss-Kruger_CM_159E	2486	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1995_Gauss-Kruger_CM_165E	2487	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1995_Gauss-Kruger_CM_171E	2488	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1995_Gauss-Kruger_CM_171W	2491	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1995_Gauss-Kruger_CM_177E	2489	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1995_Gauss-Kruger_CM_177W	2490	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1995_Gauss-Kruger_CM_21E	2463	Russia - west of 24°E onshore	54.32	19.57	55.32	22.87
Pulkovo_1995_Gauss-Kruger_CM_27E	2464	Russia - 24°E to 30°E onshore	55.69	26.61	69.47	30
Pulkovo_1995_Gauss-Kruger_CM_33E	2465	Russia - 30°E to 36°E onshore	50.34	30	70.02	36
Pulkovo_1995_Gauss-Kruger_CM_39E	2466	Russia - 36°E to 42°E onshore	43.18	36	69.23	42.01
Pulkovo_1995_Gauss-Kruger_CM_45E	2467	Russia - 42°E to 48°E onshore	41.19	42	80.91	48
Pulkovo_1995_Gauss-Kruger_CM_51E	2468	Russia - 48°E to 54°E onshore	41.39	48	81.4	54
Pulkovo_1995_Gauss-Kruger_CM_57E	2469	Russia - 54°E to 60°E onshore	50.47	54	81.91	60
Pulkovo_1995_Gauss-Kruger_CM_63E	2470	Russia - 60°E to 66°E onshore	50.66	60	81.77	66
Pulkovo_1995_Gauss-Kruger_CM_69E	2471	Russia - 66°E to 72°E onshore	54.1	66	77.07	72
Pulkovo_1995_Gauss-Kruger_CM_75E	2472	Russia - 72°E to 78°E onshore	53.17	72	79.71	78
Pulkovo_1995_Gauss-Kruger_CM_81E	2473	Russia - 78°E to 84°E onshore	50.69	78	81.03	84
Pulkovo_1995_Gauss-Kruger_CM_87E	2474	Russia - 84°E to 90°E onshore	49.07	84	81.27	90
Pulkovo_1995_Gauss-Kruger_CM_93E	2475	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1995_Gauss-Kruger_CM_99E	2476	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1995_GK_Zone_10	20010	Russia - 54°E to 60°E onshore	50.47	54	81.91	60
Pulkovo_1995_GK_Zone_10N	20070	Russia - 54°E to 60°E onshore	50.47	54	81.91	60
Pulkovo_1995_GK_Zone_11	20011	Russia - 60°E to 66°E onshore	50.66	60	81.77	66
Pulkovo_1995_GK_Zone_11N	20071	Russia - 60°E to 66°E onshore	50.66	60	81.77	66
Pulkovo_1995_GK_Zone_12	20012	Russia - 66°E to 72°E onshore	54.1	66	77.07	72
Pulkovo_1995_GK_Zone_12N	20072	Russia - 66°E to 72°E onshore	54.1	66	77.07	72
Pulkovo_1995_GK_Zone_13	20013	Russia - 72°E to 78°E onshore	53.17	72	79.71	78
Pulkovo_1995_GK_Zone_13N	20073	Russia - 72°E to 78°E onshore	53.17	72	79.71	78
Pulkovo_1995_GK_Zone_14	20014	Russia - 78°E to 84°E onshore	50.69	78	81.03	84
Pulkovo_1995_GK_Zone_14N	20074	Russia - 78°E to 84°E onshore	50.69	78	81.03	84
Pulkovo_1995_GK_Zone_15	20015	Russia - 84°E to 90°E onshore	49.07	84	81.27	90
Pulkovo_1995_GK_Zone_15N	20075	Russia - 84°E to 90°E onshore	49.07	84	81.27	90
Pulkovo_1995_GK_Zone_16	20016	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1995_GK_Zone_16N	20076	Russia - 90°E to 96°E onshore	49.89	90	81.35	96
Pulkovo_1995_GK_Zone_17	20017	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1995_GK_Zone_17N	20077	Russia - 96°E to 102°E onshore	49.73	96	81.32	102
Pulkovo_1995_GK_Zone_18	20018	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1995_GK_Zone_18N	20078	Russia - 102°E to 108°E onshore	49.64	102	79.48	108
Pulkovo_1995_GK_Zone_19	20019	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1995_GK_Zone_19N	20079	Russia - 108°E to 114°E onshore	49.14	108	76.81	114
Pulkovo_1995_GK_Zone_2	20002	Europe - 6°E to 12°E and Pulkovo by country	50.21	9.93	54.18	12
Pulkovo_1995_GK_Zone_20	20020	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1995_GK_Zone_20N	20080	Russia - 114°E to 120°E onshore	49.51	114	75.96	120
Pulkovo_1995_GK_Zone_21	20021	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1995_GK_Zone_21N	20081	Russia - 120°E to 126°E onshore	51.51	120	74	126
Pulkovo_1995_GK_Zone_22	20022	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1995_GK_Zone_22N	20082	Russia - 126°E to 132°E onshore	42.25	126	73.61	132
Pulkovo_1995_GK_Zone_23	20023	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1995_GK_Zone_23N	20083	Russia - 132°E to 138°E onshore	42.63	132	76.15	138
Pulkovo_1995_GK_Zone_24	20024	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1995_GK_Zone_24N	20084	Russia - 138°E to 144°E onshore	45.84	138	76.27	144
Pulkovo_1995_GK_Zone_25	20025	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1995_GK_Zone_25N	20085	Russia - 144°E to 150°E onshore	43.6	144	76.82	150
Pulkovo_1995_GK_Zone_26	20026	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1995_GK_Zone_26N	20086	Russia - 150°E to 156°E onshore	45.77	150	76.26	156
Pulkovo_1995_GK_Zone_27	20027	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1995_GK_Zone_27N	20087	Russia - 156°E to 162°E onshore	50.27	156	77.2	162
Pulkovo_1995_GK_Zone_28	20028	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1995_GK_Zone_28N	20088	Russia - 162°E to 168°E onshore	54.47	162	70.03	168
Pulkovo_1995_GK_Zone_29	20029	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1995_GK_Zone_29N	20089	Russia - 168°E to 174°E onshore	54.45	168	70.19	174
Pulkovo_1995_GK_Zone_2N	20062	Europe - 6°E to 12°E and Pulkovo by country	50.21	9.93	54.18	12
Pulkovo_1995_GK_Zone_3	20003	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1995_GK_Zone_30	20030	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1995_GK_Zone_30N	20090	Russia - 174°E to 180°E onshore	61.65	174	71.59	180
Pulkovo_1995_GK_Zone_31	20031	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1995_GK_Zone_31N	20091	Russia - 180° to 174°W onshore	64.35	-180	71.65	-174
Pulkovo_1995_GK_Zone_32	20032	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1995_GK_Zone_32N	20092	Russia - east of 174°W onshore	64.2	-174	67.18	-168.97
Pulkovo_1995_GK_Zone_3N	20063	Europe - 12°E to 18°E onshore and S-42(58) by country	45.78	12	54.89	18
Pulkovo_1995_GK_Zone_4	20004	Russia - west of 24°E onshore	54.32	19.57	55.32	22.87
Pulkovo_1995_GK_Zone_4N	20064	Russia - west of 24°E onshore	54.32	19.57	55.32	22.87
Pulkovo_1995_GK_Zone_5	20005	Russia - 24°E to 30°E onshore	55.69	26.61	69.47	30
Pulkovo_1995_GK_Zone_5N	20065	Russia - 24°E to 30°E onshore	55.69	26.61	69.47	30
Pulkovo_1995_GK_Zone_6	20006	Russia - 30°E to 36°E onshore	50.34	30	70.02	36
Pulkovo_1995_GK_Zone_6N	20066	Russia - 30°E to 36°E onshore	50.34	30	70.02	36
Pulkovo_1995_GK_Zone_7	20007	Russia - 36°E to 42°E onshore	43.18	36	69.23	42.01
Pulkovo_1995_GK_Zone_7N	20067	Russia - 36°E to 42°E onshore	43.18	36	69.23	42.01
Pulkovo_1995_GK_Zone_8	20008	Russia - 42°E to 48°E onshore	41.19	42	80.91	48
Pulkovo_1995_GK_Zone_8N	20068	Russia - 42°E to 48°E onshore	41.19	42	80.91	48
Pulkovo_1995_GK_Zone_9	20009	Russia - 48°E to 54°E onshore	41.39	48	81.4	54
Pulkovo_1995_GK_Zone_9N	20069	Russia - 48°E to 54°E onshore	41.39	48	81.4	54
Qatar_1948_Qatar_Grid	2099	Qatar - onshore	24.55	50.69	26.2	51.68
Qatar_National_Grid	28600	Qatar - onshore	24.55	50.69	26.2	51.68
QND_1995_Qatar_National_Grid	2932	Qatar - onshore	24.55	50.69	26.2	51.68
QND_1995_UTM_39N	102143	Qatar	24.55	50.55	27.05	53.04
Qornoq_1927_UTM_Zone_22N	2216	Greenland - southwest coast 54°W to 48°W	60.63	-54	73.05	-48
Qornoq_1927_UTM_Zone_23N	2217	Greenland - southwest coast east of 48°W	59.74	-48	62.05	-42.52
Rassadiran_Nakhl_e_Taqi	2057	Iran - Taheri refinery	27.39	52.5	27.61	52.71
RD/83_3_Degree_GK_Zone_4_E-N	5668	Germany - Saxony - west of 13.5°E	50.2	11.89	51.66	13.51
RD/83_3_Degree_GK_Zone_5_E-N	5669	Germany - Saxony - east of 13.5°E	50.62	13.5	51.58	15.04
RD/83_GK_Zone_4	3398	Germany - Saxony - west of 13.5°E	50.2	11.89	51.66	13.51
RD/83_GK_Zone_5	3399	Germany - Saxony - east of 13.5°E	50.62	13.5	51.58	15.04
RDN2008_Italy_zone	6875	Italy	34.76	5.93	47.1	18.99
RDN2008_Italy_zone_(E-N)	7794	Italy	34.76	5.93	47.1	18.99
RDN2008_TM32	6707	Italy - west of 12°E	36.53	5.94	47.04	12
RDN2008_TM33	6708	Italy - 12°E to 18°E	34.79	12	47.1	18
RDN2008_TM34	6709	Italy - east of 18°E	34.76	17.99	41.64	18.99
RDN2008_UTM_zone_32N	7791	Italy - west of 12°E	36.53	5.94	47.04	12
RDN2008_UTM_zone_33N	7792	Italy - 12°E to 18°E	34.79	12	47.1	18
RDN2008_UTM_zone_34N	7793	Italy - east of 18°E	34.76	17.99	41.64	18.99
RDN2008_Zone_12	6876	Italy	34.76	5.93	47.1	18.99
RDN2008_Zone_12_(E-N)	7795	Italy	34.76	5.93	47.1	18.99
RD_New	28992	Netherlands - onshore	50.75	3.2	53.7	7.22
RD_Old	28991	Netherlands - onshore	50.75	3.2	53.7	7.22
REGCAN95_LAEA_Europe	5635	Spain - Canary Islands	24.6	-21.93	32.76	-11.75
REGCAN95_LCC_Europe	5634	Spain - Canary Islands	24.6	-21.93	32.76	-11.75
REGCAN95_UTM_Zone_27N	4082	Spain - Canary Islands - west of 18°W	24.6	-21.93	31.19	-18
REGCAN95_UTM_Zone_28N	4083	Spain - Canary Islands - east of 18°W	25.25	-18	32.76	-11.75
REGVEN_UTM_Zone_18N	2201	Venezuela - west of 72°W	7.02	-73.38	11.62	-71.99
REGVEN_UTM_Zone_19N	2202	Venezuela - 72°W and 66°W	0.73	-72	15.64	-66
REGVEN_UTM_Zone_20N	2203	Venezuela - east of 66°W	0.64	-66	16.75	-58.95
Reunion_1947_TM_Reunion	3727	Reunion - onshore	-21.42	55.16	-20.81	55.91
RGAF09_UTM_Zone_20N	5490	Caribbean - French Antilles west of 60°W	14.08	-63.66	18.31	-60
RGF_1993_CC42	3942	France - mainland south of 43°N and Corsica	41.31	-1.06	43.07	9.63
RGF_1993_CC43	3943	France - mainland south of 44°N	42.33	-1.79	44.01	7.65
RGF_1993_CC44	3944	France - mainland - 43°N to 45°N	42.92	-1.79	45	7.71
RGF_1993_CC45	3945	France - mainland - 44°N to 46°N	44	-1.46	46	7.71
RGF_1993_CC46	3946	France - mainland - 45°N to 47°N	45	-2.21	47	7.16
RGF_1993_CC47	3947	France - mainland - 46°N to 48°N	46	-4.77	48	7.63
RGF_1993_CC48	3948	France - mainland - 47°N to 49°N	47	-4.87	49	8.23
RGF_1993_CC49	3949	France - mainland - 48°N to 50°N	48	-4.87	50	8.23
RGF_1993_CC50	3950	France - mainland north of 49°N	49	-2.03	51.14	8.08
RGF_1993_Lambert_93	2154	France	41.15	-9.86	51.56	10.38
RGFG_1995_UTM_22N	2972	French Guiana - east of 54°W	2.17	-54	8.88	-49.45
RGFG_1995_UTM_Zone_21N	3313	French Guiana - west of 54°W	2.11	-54.61	5.69	-54
RGM_2004_UTM_Zone_38S	4471	Mayotte	-14.49	43.68	-11.33	46.7
RGNC_1991_93_Lambert_New_ Caledonia	3163	New Caledonia - Belep, Grande Terre, Ile des Pins, Loyalty Islands	-22.73	163.54	-19.5	168.19
RGNC_1991-93_UTM_Zone_57S	3169	New Caledonia - west of 162°E	-26.03	156.25	-15.34	162.01
RGNC_1991-93_UTM_Zone_58S	3170	New Caledonia - 162°E to 168°E	-26.45	162	-14.83	168
RGNC_1991-93_UTM_Zone_59S	3171	New Caledonia - east of 168°E	-25.95	168	-19.75	174.28
RGNC_1991_Lambert_New_Caledonia	2984	New Caledonia	-26.45	156.25	-14.83	174.28
RGPF_UTM_Zone_5S	3296	French Polynesia - west of 150°W	-26.7	-158.13	-12.5	-150
RGPF_UTM_Zone_6S	3297	French Polynesia - 150°W to 144°W	-31.2	-150	-7.29	-144
RGPF_UTM_Zone_7S	3298	French Polynesia - 144°W to 138°W	-31.24	-144	-4.52	-138
RGPF_UTM_Zone_8S	3299	French Polynesia - east of 138°W	-26.58	-138	-5.52	-131.97
RGR_1992_UTM_39S	5644	Reunion - west of 54°E	-24.37	51.83	-18.52	54
RGR_1992_UTM_40S	2975	Reunion - east of 54°E	-24.72	54	-18.28	58.24
RGRDC_2005_Congo_TM_Zone_12	4048	Congo DR (Zaire) - 11°E to 13°E	-6.04	11.79	-4.67	13
RGRDC_2005_Congo_TM_Zone_14	4049	Congo DR (Zaire) - 13°E to 15°E	-5.91	13	-4.28	15.01
RGRDC_2005_Congo_TM_Zone_16	4050	Congo DR (Zaire) - south and 15°E to 17°E	-7.31	15	-3.41	17
RGRDC_2005_Congo_TM_Zone_18	4051	Congo DR (Zaire) - south and 17°E and 19°E	-8.11	17	-3.43	19
RGRDC_2005_Congo_TM_Zone_20	4056	Congo DR (Zaire) - south and 19°E to 21°E	-8	19	-3.77	21
RGRDC_2005_Congo_TM_Zone_22	4057	Congo DR (Zaire) - south and 21°E to 23°E	-11.24	21	-4.18	23.01
RGRDC_2005_Congo_TM_Zone_24	4058	Congo DR (Zaire) - south and 23°E to 25°E	-11.47	23	-4.58	25
RGRDC_2005_Congo_TM_Zone_26	4059	Congo DR (Zaire) - south and 25°E to 27°E	-11.99	25	-4.99	27
RGRDC_2005_Congo_TM_Zone_28	4060	Congo DR (Zaire) - south and 27°E to 29°E	-13.39	27	-6.43	29
RGRDC_2005_Congo_TM_Zone_30	5844	Congo DR (Zaire) - south and 29°E to 31°E	-13.46	29	-12.15	29.81
RGRDC_2005_UTM_Zone_33S	4061	Congo DR (Zaire) - south and 12°E to 18°E	-8.11	12	-3.41	18.01
RGRDC_2005_UTM_Zone_34S	4062	Congo DR (Zaire) - south and 18°E to 24°E	-11.24	18	-3.57	24
RGRDC_2005_UTM_Zone_35S	4063	Congo DR (Zaire) - south and 24°E to 30°E	-13.46	24	-4.79	29.81
RGSPM_2006_UTM_Zone_21N	4467	St Pierre and Miquelon	43.41	-57.1	47.37	-55.9
RGTAAF07_Terre_Adelie_Polar_ Stereographic	7082	Antarctica - Adelie Land coastal area	-67.13	136	-65.61	142
RGTAAF07_UTM_zone_37S	7074	French Southern Territories - Europa	-25.7	37.98	-20.91	41.82
RGTAAF07_UTM_zone_38S	7075	French Southern Territories - Crozet west of 48°E	-49.38	45.37	-43.12	48.01
RGTAAF07_UTM_zone_39S	7076	French Southern Territories - Crozet 48°E to 54°E	-49.82	48	-42.61	54.01
RGTAAF07_UTM_zone_40S	7077	French Southern Territories - Crozet east of 54°E	-49.61	54	-43.3	57.16
RGTAAF07_UTM_zone_41S	7078	French Southern Territories - 60°E to 66°E	-53.03	62.96	-45.73	66
RGTAAF07_UTM_zone_42S	7079	French Southern Territories - 66°E to 72°E	-53.24	66	-45.11	72.01
RGTAAF07_UTM_zone_43S	7080	French Southern Territories - 72°E to 78°E	-51.19	72	-34.47	78.01
RGTAAF07_UTM_zone_44S	7081	French Southern Territories - east of 78°E	-42.04	78	-34.5	81.83
RGTAAF07_UTM_Zone_53S	8455	Antarctica - Adelie Land coastal area west of 138°E	-66.73	136	-65.61	138.01
RGTAAF07_UTM_Zone_54S	8456	Antarctica - Adelie Land coastal area east of 138°E	-67.13	138	-66.1	142
RGWF96_UTM_Zone_1S	8903	Wallis and Futuna	-15.94	179.49	-9.84	-174.27
Roma_1940_Gauss_Boaga_Est	102093	Italy - east of 12°E	34.76	12	47.1	18.99
Roma_1940_Gauss_Boaga_Ovest	102094	Italy - west of 12°E	36.53	5.94	47.04	12
RRAF_1991_UTM_20N	4559	Caribbean - French Antilles west of 60°W	14.08	-63.66	18.31	-60
RSAO13_TM_12_SE	9159	Angola - Angola proper - offshore	-17.26	8.2	-6.01	13.86
RSAO13_UTM_Zone_32S	9156	Angola - west of 12°E	-17.28	8.2	-5.03	12.01
RSAO13_UTM_Zone_33S	9157	Angola - 12°E to 18°E	-17.44	12	-4.38	18
RSAO13_UTM_Zone_34S	9158	Angola - east of 18°E	-18.02	17.99	-6.91	24.09
RSRGD2000_BCLC2000	5480	Antarctica - Borchgrevink Coast region	-76	157	-73	173
RSRGD2000_DGLC2000	3852	Antarctica - Darwin Glacier region	-81	145	-76	169
RSRGD2000_MSLC2000	5479	Antarctica - McMurdo Sound region	-81	153	-76	173
RSRGD2000_PCLC2000	5481	Antarctica - Pennell Coast region	-73	160	-69.5	172
RSRGD2000_RSPS2000	5482	Antarctica - Ross Ice Shelf Region	-90	150	-76	-150
RT38_0_gon	3028	Sweden - 0 gon	56.86	16.08	68.54	20.22
RT38_25_gon_O	3029	Sweden - 2.5 gon E	63.37	18.4	69.07	22.2
RT38_25_gon_V	3027	Sweden - 2.5 gon W	55.95	13.66	67.18	17.73
RT38_5_gon_O	3030	Sweden - 5 gon E	65.24	21.34	68.58	24.17
RT38_5_gon_V	3026	Sweden - 5 gon W	55.28	11.81	64.39	15.44
RT38_75_gon_V	3025	Sweden - 7.5 gon W	57.29	10.93	59.73	12.91
RT90_0_gon	3022	Sweden - 0 gon	56.86	16.08	68.54	20.22
RT90_25_gon_O	3023	Sweden - 2.5 gon E	63.37	18.4	69.07	22.2
RT90_25_gon_V	3021	Sweden - 2.5 gon W	55.95	13.66	67.18	17.73
RT90_25_gon_W	2400	Sweden	54.96	10.03	69.07	24.17
RT90_5_gon_O	3024	Sweden - 5 gon E	65.24	21.34	68.58	24.17
RT90_5_gon_V	3020	Sweden - 5 gon W	55.28	11.81	64.39	15.44
RT90_75_gon_V	3019	Sweden - 7.5 gon W	57.29	10.93	59.73	12.91
SAD_1969_96_Brazil_Polyconic	5530	Brazil - SAD69	-35.71	-60.57	7.04	-29.03
SAD_1969_96_UTM_Zone_18S	5875	Brazil - west of 72°W	-10.01	-74.01	-4.59	-71.99
SAD_1969_96_UTM_Zone_19S	5876	Brazil - 72°W to 66°W	-11.14	-72	2.15	-65.99
SAD_1969_96_UTM_Zone_20S	5877	Brazil - 66°W to 60°W	-16.28	-66	5.28	-59.99
SAD_1969_96_UTM_Zone_21S	5531	Brazil - 60°W to 54°W	-31.91	-60	4.51	-53.99
SAD_1969_96_UTM_Zone_22S	5858	Brazil - 54°W to 48°W and SAD69	-35.71	-54.01	7.04	-47.99
SAD_1969_96_UTM_Zone_23S	5533	Brazil - 48°W to 42°W	-33.5	-48	5.13	-42
SAD_1969_96_UTM_Zone_24S	5534	Brazil - 42°W to 36°W	-26.35	-42	0.74	-36
SAD_1969_96_UTM_Zone_25S	5535	Brazil - 36°W to 30°W	-23.8	-36	4.19	-29.99
SAD_1969_Brazil_Polyconic	29101	Brazil	-35.71	-74.01	7.04	-25.28
SAD_1969_UTM_Zone_17N	5463	South America - 84°W to 78°W, N hemisphere and SAD69 by country	0	-80.18	2.7	-78
SAD_1969_UTM_Zone_17S	29187	South America - 84°W to 78°W, S hemisphere and SAD69 by country	-10.53	-81.41	0	-78
SAD_1969_UTM_Zone_18N	29168	South America - 78°W to 72°W, N hemisphere and SAD69 by country	0	-78	12.31	-72
SAD_1969_UTM_Zone_18S	29188	South America - 78°W to 72°W, S hemisphere and SAD69 by country	-45	-78	0	-71.99
SAD_1969_UTM_Zone_19N	29169	South America - 72°W to 66°W, N hemisphere onshore	0	-72	12.52	-66
SAD_1969_UTM_Zone_19S	29189	South America - 72°W to 66°W, S hemisphere onshore	-45	-72	2.15	-65.99
SAD_1969_UTM_Zone_20N	29170	South America - 66°W to 60°W, N hemisphere and SAD69 by country	0.64	-66	11.23	-59.99
SAD_1969_UTM_Zone_20S	29190	South America - 66°W to 60°W, S hemisphere and SAD69 by country	-45	-66	5.28	-59.99
SAD_1969_UTM_Zone_21N	29171	South America - 60°W to 54°W, N hemisphere and SAD69 by country	1.18	-60	8.6	-54
SAD_1969_UTM_Zone_21S	29191	South America - 60°W to 54°W, S hemisphere and SAD69 by country	-38.91	-60	4.51	-53.99
SAD_1969_UTM_Zone_22N	29172	South America - 54°W to 48°W, N hemisphere and SAD69 by country	1.68	-54	5.81	-46.65
SAD_1969_UTM_Zone_22S	29192	South America - 54°W to 48°W, S hemisphere and SAD69 by country	-35.71	-54	7.04	-47.99
SAD_1969_UTM_Zone_23S	29193	Brazil - 48°W to 42°W	-33.5	-48	5.13	-42
SAD_1969_UTM_Zone_24S	29194	Brazil - 42°W to 36°W	-26.35	-42	0.74	-36
SAD_1969_UTM_Zone_25S	29195	Brazil - 36°W to 30°W	-23.8	-36	4.19	-29.99
Sahara	26193	Morocco - south of 27.9°N	21.06	-17	27.9	-8.67
Sahara_Degree	102193	Morocco - south of 27.9°N	21.06	-17	27.9	-8.67
Sainte_Anne_UTM_20N	2970	Guadeloupe - Grande- Terre and surrounding islands - onshore	15.8	-61.85	16.55	-60.97
Saint_Pierre_et_Miquelon_1950_UTM_ 21N	2987	St Pierre and Miquelon - onshore	46.69	-56.48	47.19	-56.07
Saipan_Az_Eq_1969	102238	Northern Mariana Islands	12.38	141.33	23.9	149.55
Samboja_UTM_Zone_50S	2550	Indonesia - Kalimantan - Mahakam delta	-1.24	116.72	0	117.99
Samoa_1962_Samoa_Lambert	3102	American Samoa - 2 main island groups	-14.43	-170.88	-14.11	-169.38
Sao_Braz_UTM_Zone_26N	102168	Portugal - Azores E - onshore	36.87	-25.92	37.96	-24.62
Sapper_Hill_1943_UTM_Zone_20S	29220	Falkland Islands - onshore west of 60°W	-52.33	-61.55	-50.96	-59.99
Sapper_Hill_1943_UTM_Zone_21S	29221	Falkland Islands - onshore east of 60°W	-52.51	-60	-51.13	-57.6
Schwarzeck_UTM_Zone_33S	29333	Namibia - offshore	-30.64	8.24	-17.24	16.46
Selvagem_Grande_1938_UTM_Zone_28N	2943	Portugal - Selvagens onshore	29.98	-16.11	30.21	-15.79
SHMG2015	7887	St Helena - St Helena Island	-16.08	-5.85	-15.85	-5.58
Sibun_Gorge_1922_Colony_Grid	5589	Belize - onshore	15.88	-89.22	18.49	-87.72
Sierra_Leone_1924_New_Colony_Grid	2159	Sierra Leone - Freetown Peninsula	8.32	-13.34	8.55	-13.13
Sierra_Leone_1924_New_War_Office_ Grid	2160	Sierra Leone - Freetown Peninsula	8.32	-13.34	8.55	-13.13
Sierra_Leone_1968_UTM_Zone_28N	2161	Sierra Leone - west of 12°W	7.15	-13.35	9.94	-12
Sierra_Leone_1968_UTM_Zone_29N	2162	Sierra Leone - east of 12°W	6.88	-12	10	-10.26
SIRGAS_2000_Brazil_Mercator	5641	Brazil - equatorial margin	-5.74	-51.64	7.04	-32.43
SIRGAS_2000_Brazil_Polyconic	5880	Brazil	-35.71	-74.01	7.04	-25.28
SIRGAS_2000_UTM_Zone_11N	31965	Latin America - 120°W to 114°W	15.01	-120	32.72	-114
SIRGAS_2000_UTM_Zone_12N	31966	Latin America - 114°W to 108°W	15.09	-114	32.27	-108
SIRGAS_2000_UTM_Zone_13N	31967	Latin America - 108°W to 102°W	14.05	-108	31.79	-102
SIRGAS_2000_UTM_Zone_14N	31968	Latin America - 102°W to 96°W	12.3	-102.01	29.81	-96
SIRGAS_2000_UTM_Zone_15N	31969	Latin America - 96°W to 90°W; N hemisphere and SIRGAS 2000 by country	0	-96	26	-90
SIRGAS_2000_UTM_Zone_16N	31970	Latin America - 90°W to 84°W; N hemisphere and SIRGAS 2000 by country	0	-90	25.77	-83.99
SIRGAS_2000_UTM_Zone_17N	31971	Latin America - 84°W to 78°West; N hemisphere and SIRGAS by country	0	-84	19.54	-78
SIRGAS_2000_UTM_Zone_17S	31977	South America - 84°W to 78°W, S hemisphere	-56.45	-84	0	-78
SIRGAS_2000_UTM_Zone_18N	31972	Latin America - 78°W to 72°West; N hemisphere and SIRGAS by country	0	-78	15.04	-72
SIRGAS_2000_UTM_Zone_18S	31978	South America - 78°W to 72°W, S hemisphere and SIRGAS 2000 by country	-59.36	-78	0	-71.99
SIRGAS_2000_UTM_Zone_19N	31973	South America - 72°W to 66°W, N hemisphere and SIRGAS 2000 by country	0	-72	15.64	-66
SIRGAS_2000_UTM_Zone_19S	31979	South America - 72°W to 66°W, S hemisphere and SIRGAS 2000 by country	-59.87	-72	2.15	-66
SIRGAS_2000_UTM_Zone_20N	31974	South America - 66°W to 60°W, N hemisphere and SIRGAS 2000 by country	0.64	-66	16.75	-59.99
SIRGAS_2000_UTM_Zone_20S	31980	South America - 66°W to 60°W, S hemisphere and SIRGAS 2000 by country	-58.39	-66	5.28	-60
SIRGAS_2000_UTM_Zone_21N	31975	South America - 60°W to 54°W, N hemisphere and SIRGAS 2000 by country	1.18	-60	12.19	-54
SIRGAS_2000_UTM_Zone_21S	31981	South America - 60°W to 54°W, S hemisphere and SIRGAS 2000 by country	-44.82	-60	4.51	-54
SIRGAS_2000_UTM_Zone_22N	31976	South America - 54°W to 48°W, N hemisphere and SIRGAS 2000 by country	0	-54	9.24	-47.99
SIRGAS_2000_UTM_Zone_22S	31982	South America - 54°W to 48°W, S hemisphere and SIRGAS 2000 by country	-54.18	-54	7.04	-47.99
SIRGAS_2000_UTM_Zone_23N	6210	Brazil - 48°W to 42°W and north of 0°N	0	-48	5.13	-41.99
SIRGAS_2000_UTM_Zone_23S	31983	Brazil - 48°W to 42°W	-33.5	-48	5.13	-42
SIRGAS_2000_UTM_Zone_24N	6211	Brazil - 42°W to 36°W and north of 0°N	0	-42	0.74	-38.22
SIRGAS_2000_UTM_Zone_24S	31984	Brazil - 42°W to 36°W	-26.35	-42	0.74	-36
SIRGAS_2000_UTM_Zone_25S	31985	Brazil - 36°W to 30°W	-23.8	-36	4.19	-29.99
SIRGAS_2000_UTM_Zone_26S	5396	Brazil - east of 30°W	-23.86	-30	4.26	-25.28
SIRGAS-Chile_2010_UTM_Zone_18S	8950	Chile - 78°W to 72°W	-59.36	-78	-18.35	-71.99
SIRGAS-Chile_2010_UTM_Zone_19S	8951	Chile - 72°W to 66°W	-59.87	-72	-17.5	-66
SIRGAS-Chile_2013_UTM_Zone_18S	9149	Chile - 78°W to 72°W	-59.36	-78	-18.35	-71.99
SIRGAS-Chile_2013_UTM_Zone_19S	9150	Chile - 72°W to 66°W	-59.87	-72	-17.5	-66
SIRGAS-Chile_2016_UTM_Zone_18S	9154	Chile - 78°W to 72°W	-59.36	-78	-18.35	-71.99
SIRGAS-Chile_2016_UTM_Zone_19S	9155	Chile - 72°W to 66°W	-59.87	-72	-17.5	-66
SIRGAS-Chile_UTM_Zone_18S	5362	Chile - 78°W to 72°W	-59.36	-78	-18.35	-71.99
SIRGAS-Chile_UTM_Zone_19S	5361	Chile - 72°W to 66°W	-59.87	-72	-17.5	-66
SIRGAS-ROU98_UTM_Zone_21S	5382	Uruguay - west of 54°W	-36.63	-58.49	-30.09	-54
SIRGAS-ROU98_UTM_Zone_22S	5383	Uruguay - east of 54°W	-37.77	-54	-31.9	-50.01
SIRGAS_UTM_Zone_17N	31986	South America - 84°W to 78°W, N hemisphere and SIRGAS95 by country	0.9	-84	15.51	-78
SIRGAS_UTM_Zone_17S	31992	South America - 84°W to 78°W, S hemisphere and SIRGAS95 by country	-56.45	-84	1.45	-75.21
SIRGAS_UTM_Zone_18N	31987	South America - 78°W to 72°W, N hemisphere	0	-78	15.04	-72
SIRGAS_UTM_Zone_18S	31993	South America - 78°W to 72°W, S hemisphere and SIRGAS 1995 by country	-59.36	-78	0	-71.99
SIRGAS_UTM_Zone_19N	31988	South America - 72°W to 66°W, N hemisphere	0	-72	15.64	-66
SIRGAS_UTM_Zone_19S	31994	South America - 72°W to 66°W, S hemisphere	-59.87	-72	0	-66
SIRGAS_UTM_Zone_20N	31989	South America - 66°W to 60°W, N hemisphere	0	-66	16.75	-60
SIRGAS_UTM_Zone_20S	31995	South America - 66°W to 60°W, S hemisphere	-58.39	-66	0	-60
SIRGAS_UTM_Zone_21N	31990	South America - 60°W to 54°W, N hemisphere	0	-60	10.7	-54
SIRGAS_UTM_Zone_21S	31996	South America - 60°W to 54°W, S hemisphere	-44.82	-60	0	-54
SIRGAS_UTM_Zone_22N	31991	South America - 54°W to 48°W, N hemisphere	0	-54	9.24	-48
SIRGAS_UTM_Zone_22S	31997	South America - 54°W to 48°W, S hemisphere	-39.95	-54	0	-48
SIRGAS_UTM_Zone_23S	31998	South America - 48°W to 42°W	-33.5	-48	0	-42
SIRGAS_UTM_Zone_24S	31999	South America - 42°W to 36°W	-26.35	-42	0	-36
SIRGAS_UTM_Zone_25S	32000	South America - 36°W to 30°W	-20.11	-36	0	-30
Sister_Islands_National_Grid_1961	6129	Cayman Islands - Little Cayman and Cayman Brac	19.63	-80.14	19.78	-79.69
S-JTSK_Ferro_Krovak	2065	Europe - Czechoslovakia	47.73	12.09	51.06	22.56
S-JTSK_Ferro_Krovak_East_North	5221	Europe - Czechoslovakia	47.73	12.09	51.06	22.56
S-JTSK_Krovak	5513	Europe - Czechoslovakia	47.73	12.09	51.06	22.56
S-JTSK_Krovak_East_North	5514	Europe - Czechoslovakia	47.73	12.09	51.06	22.56
S-JTSK_[JTSK03]_Krovak	8352	Slovakia	47.73	16.84	49.61	22.56
S-JTSK_[JTSK03]_Krovak_East_North	8353	Slovakia	47.73	16.84	49.61	22.56
SLD99_Sri_Lanka_Grid_1999	5235	Sri Lanka - onshore	5.86	79.64	9.88	81.95
Slovenia_1996_Slovene_National_Grid	3794	Slovenia	45.42	13.38	46.88	16.61
Slovenia_1996_UTM_Zone_33N	8687	Slovenia	45.42	13.38	46.88	16.61
South_America_Albers_Equal_Area_ Conic	102033	South America	-60	-90	15	-30
South_America_Equidistant_Conic	102032	South America	-60	-90	15	-30
South_America_Lambert_Conformal_ Conic	102015	South America	-60	-90	15	-30
South_East_Island_1943_UTM_Zone_ 40N	6915	Seychelles - Seychelles Bank	-4.86	55.15	-3.66	56.01
South_Pole_Azimuthal_Equidistant	102019	World - south of 0°N	-90	-180	0	180
South_Pole_Gnomonic	102036	World - south of 0°N	-90	-180	0	180
South_Pole_Lambert_Azimuthal_Equal_ Area	102020	World - south of 0°N	-90	-180	0	180
South_Pole_Orthographic	102037	World - south of 0°N	-90	-180	0	180
South_Pole_Stereographic	102021	World - south of 0°N	-90	-180	0	180
South_Yemen_GK_Zone_8	2395	Yemen - South Yemen - mainland west of 48°E	12.54	43.37	17.95	48.01
South_Yemen_GK_Zone_9	2396	Yemen - South Yemen - mainland east of 48°E	13.94	48	19	53.14
Sphere_Aitoff	53043	World	-90	-180	90	180
Sphere_Azimuthal_Equidistant	53032	World	-90	-180	90	180
Sphere_Behrmann	53017	World	-90	-180	90	180
Sphere_Bonne	53024	World	-90	-180	90	180
Sphere_Cassini	53028	World	-90	-180	90	180
Sphere_Compact_Miller	53080	World	-90	-180	90	180
Sphere_Craster_Parabolic	53046	World	-90	-180	90	180
Sphere_Cylindrical_Equal_Area	53034	World	-90	-180	90	180
Sphere_Eckert_I	53015	World	-90	-180	90	180
Sphere_Eckert_II	53014	World	-90	-180	90	180
Sphere_Eckert_III	53013	World	-90	-180	90	180
Sphere_Eckert_IV	53012	World	-90	-180	90	180
Sphere_Eckert_V	53011	World	-90	-180	90	180
Sphere_Eckert_VI	53010	World	-90	-180	90	180
Sphere_Equal_Earth_Greenwich	53035	World	-90	-180	90	180
Sphere_Equal_Earth_Americas	53036	World	-90	-180	90	180
Sphere_Equal_Earth_Asia_Pacific	53037	World	-90	-180	90	180
Sphere_Equidistant_Conic	53027	World	-90	-180	90	180
Sphere_Equidistant_Cylindrical	53002	World	-90	-180	90	180
Sphere_Flat_Polar_Quartic	53045	World	-90	-180	90	180
Sphere_Gall_Stereographic	53016	World	-90	-180	90	180
Sphere_Hammer_Aitoff	53044	World	-90	-180	90	180
Sphere_Hotine	53025	World	-90	-180	90	180
Sphere_Loximuthal	53023	World	-90	-180	90	180
Sphere_Mercator	53004	World	-90	-180	90	180
Sphere_Miller_Cylindrical	53003	World	-90	-180	90	180
Sphere_Mollweide	53009	World	-90	-180	90	180
Sphere_Natural_Earth	53077	World	-90	-180	90	180
Sphere_Natural_Earth_II	53078	World	-90	-180	90	180
Sphere_Patterson	53079	World	-90	-180	90	180
Sphere_Plate_Carree	53001	World	-90	-180	90	180
Sphere_Polyconic	53021	World	-90	-180	90	180
Sphere_Quartic_Authalic	53022	World	-90	-180	90	180
Sphere_Robinson	53030	World	-90	-180	90	180
Sphere_Sinusoidal	53008	World	-90	-180	90	180
Sphere_Stereographic	53026	World	-90	-180	90	180
Sphere_Times	53048	World	-90	-180	90	180
Sphere_Two_Point_Equidistant	53031	World	-90	-180	90	180
Sphere_Van_der_Grinten_I	53029	World	-90	-180	90	180
Sphere_Vertical_Perspective	53049	World	-90	-180	90	180
Sphere_Wagner_IV	53074	World	-90	-180	90	180
Sphere_Wagner_V	53075	World	-90	-180	90	180
Sphere_Wagner_VII	53076	World	-90	-180	90	180
Sphere_Winkel_I	53018	World	-90	-180	90	180
Sphere_Winkel_II	53019	World	-90	-180	90	180
Sphere_Winkel_Tripel_NGS	53042	World	-90	-180	90	180
SRB_ETRS89_UTM_zone_34N	8682	Serbia and Kosovo	41.85	18.81	46.19	23.01
ST71_Belep_UTM_58S	2997	New Caledonia - Belep	-19.85	163.54	-19.5	163.75
ST84_Ile_des_Pins_UTM_58S	2996	New Caledonia - Ile des Pins	-22.73	167.36	-22.49	167.61
ST87_Ouvea_UTM_58S	3164	New Caledonia - Ouvea	-20.77	166.44	-20.34	166.71
Stereo_33	31600	Romania - onshore	43.62	20.26	48.27	29.74
Stereo_70	31700	Romania	43.44	20.26	48.27	31.41
St_Helena_Tritan_SHLG(Tritan)	7882	St Helena - St Helena Island	-16.08	-5.85	-15.85	-5.58
St_Helena_Tritan_UTM_zone_30S	7883	St Helena - St Helena Island	-16.08	-5.85	-15.85	-5.58
St_Kitts_1955_British_West_Indies_Grid	2005	St Kitts and Nevis - onshore	17.06	-62.92	17.46	-62.5
St_Lucia_1955_British_West_Indies_Grid	2006	St Lucia - onshore	13.66	-61.13	14.16	-60.82
St_Vincent_1945_British_West_Indies_ Grid	2007	St Vincent and the Grenadines - onshore	12.54	-61.52	13.44	-61.07
Sud_Algerie_Ancienne	30492	Algeria - 31°30'N to 34°39'N	31.49	-3.85	34.66	9.22
Sud_Algerie_Ancienne_Degree	102492	Algeria	18.97	-8.67	38.8	11.99
Sudan_UTM_Zone_35N	29635	Sudan - south - west of 30°E	3	22	22	30
Sudan_UTM_Zone_36N	29636	Sudan - south - east of 30°E	3	30	22	38.5
Sud_Maroc	26192	Morocco - south of 31.5°N	27.66	-13.24	31.51	-3.59
Sud_Maroc_Degree	102192	Morocco - south of 31.5°N	27.66	-13.24	31.51	-3.59
Sud_Tunisie	22392	Tunisia - south of 34°39'N	30.23	7.49	34.66	11.59
SVY21_Singapore_TM	3414	Singapore	1.13	103.59	1.47	104.07
SWEREF99_12_00	3007	Sweden - 12 00	56.74	10.93	60.13	13.11
SWEREF99_13_30	3008	Sweden - 13 30	55.28	12.12	62.28	14.79
SWEREF99_14_15	3012	Sweden - 14 15	61.55	11.93	64.39	15.55
SWEREF99_15_00	3009	Sweden - 15 00	55.95	13.54	61.62	16.15
SWEREF99_15_45	3013	Sweden - 15 45	60.44	13.66	65.13	17.01
SWEREF99_16_30	3010	Sweden - 16 30	56.15	15.41	62.26	17.63
SWEREF99_17_15	3014	Sweden - 17 15	62.12	14.31	67.19	19.04
SWEREF99_18_00	3011	Sweden - 18 00	58.66	17.08	60.7	19.61
SWEREF99_18_45	3015	Sweden - 18 45	56.86	17.18	66.17	20.22
SWEREF99_20_15	3016	Sweden - 20 15	63.45	16.08	69.07	23.28
SWEREF99_21_45	3017	Sweden - 21 45	65.01	19.63	66.43	22.91
SWEREF99_23_15	3018	Sweden - 23 15	65.49	21.85	68.14	24.17
SWEREF99_County_ST74	3854	Sweden - Stockholm county	58.69	17.25	60.27	19.61
SWEREF99_RT90_0_gon_emulation	3848	Sweden - 0 gon	56.86	16.08	68.54	20.22
SWEREF99_RT90_2.5_gon_O_emulation	3849	Sweden - 2.5 gon E	63.37	18.4	69.07	22.2
SWEREF99_RT90_2.5_gon_V_emulation	3847	Sweden - 2.5 gon W	55.95	13.66	67.18	17.73
SWEREF99_RT90_5_gon_O_emulation	3850	Sweden - 5 gon E	65.24	21.34	68.58	24.17
SWEREF99_RT90_5_gon_V_emulation	3846	Sweden - 5 gon W	55.28	11.81	64.39	15.44
SWEREF99_RT90_7.5_gon_V_emulation	3845	Sweden - 7.5 gon W	57.29	10.93	59.73	12.91
SWEREF99_TM	3006	Sweden	54.96	10.03	69.07	24.17
Tahaa_1954_UTM_5S	2977	French Polynesia - Society Islands - Bora Bora, Huahine, Raiatea, Tahaa	-16.96	-151.91	-16.17	-150.89
Tahiti_1952_UTM_6S	2976	French Polynesia - Society Islands - Moorea and Tahiti	-17.93	-150	-17.41	-149.11
Tahiti_1979_UTM_Zone_6S	3304	French Polynesia - Society Islands - Tahiti	-17.93	-149.7	-17.44	-149.09
Tananarive_1925_Laborde_Grid	8441	Madagascar - onshore	-25.64	43.18	-11.89	50.56
Tananarive_1925_Paris_Laborde_Grid	29701	Madagascar - onshore	-25.64	43.18	-11.89	50.56
Tananarive_1925_UTM_Zone_38S	29738	Madagascar - nearshore - west of 48°E	-26.59	42.53	-13	48
Tananarive_1925_UTM_Zone_39S	29739	Madagascar - nearshore - east of 48°E	-24.21	48	-11.69	51.03
Tapi_Aike_Argentina_1	9249	Argentina - south Santa Cruz west of 70.5°W	-52	-73.28	-50.33	-70.5
Tapi_Aike_Argentina_2	9250	Argentina - south Santa Cruz east of 70.5°W	-52.43	-70.5	-50.33	-68.3
TC_1948_UTM_Zone_39N	30339	UAE - Abu Dhabi - onshore west of 54°E	22.76	51.56	24.32	54.01
TC_1948_UTM_Zone_40N	30340	UAE - Abu Dhabi and Dubai - onshore east of 54°E	22.63	53.99	25.34	56.03
Tete_UTM_Zone_36S	2736	Mozambique - onshore west of 36°E	-26.87	30.21	-11.41	36
Tete_UTM_Zone_37S	2737	Mozambique - onshore east of 36°E	-18.98	35.99	-10.42	40.9
TGD2005_Tonga_Map_Grid	5887	Tonga	-25.68	-179.08	-14.14	-171.28
The_World_From_Space	102038	World	-90	-180	90	180
Timbalai_1948_RSO_Borneo_Chains	29871	Asia - Brunei and East Malaysia	0.85	109.31	7.67	119.61
Timbalai_1948_RSO_Borneo_Feet	29872	Malaysia - East Malaysia onshore	0.85	109.54	7.41	119.33
Timbalai_1948_RSO_Borneo_Meters	29873	Asia - Brunei and East Malaysia	0.85	109.31	7.67	119.61
Timbalai_1948_UTM_Zone_49N	29849	Asia - Brunei and East Malaysia - 108°E to 114°E	0.85	109.31	7.37	114
Timbalai_1948_UTM_Zone_50N	29850	Asia - Brunei and East Malaysia - 114°E to 120°E	1.43	114	7.67	119.61
TM65_Irish_Grid	29902	Ireland - onshore	51.39	-10.56	55.43	-5.93
TM75_Irish_Grid	29903	Europe - Ireland (Republic and Ulster) - onshore	51.39	-10.56	55.43	-5.34
Tokyo_UTM_Zone_51N	3092	Japan - 120°E to 126°E onshore	23.98	123.62	24.94	125.51
Tokyo_UTM_Zone_52N	3093	Japan - 126°E to 132°E onshore	24.4	126.63	34.9	132
Tokyo_UTM_Zone_53N	3094	Japan - 132°E to 138°E onshore	20.37	132	37.58	138
Tokyo_UTM_Zone_54N	3095	Japan - 138°E to 144°E onshore	24.67	138	45.54	144
Tokyo_UTM_Zone_55N	3096	Japan - 144°E to 150°E onshore	42.84	144	44.4	145.87
Tokyo_UTM_Zone_56N	102156	World - N hemisphere - 150°E to 156°E	0	150	84	156
TPEN11_Grid	9367	UK - Liverpool to Leeds	53.32	-3.14	53.9	-1.35
Trinidad_1903_Trinidad_Grid	30200	Trinidad and Tobago - Trinidad	9.83	-62.09	11.51	-60
Trinidad_1903_Trinidad_Grid_Feet_ Clarke	2314	Trinidad and Tobago - Trinidad	9.83	-62.09	11.51	-60
TUREF_3_Degree_GK_Zone_10	5270	Turkey - 28.5°E to 31.5°E onshore	36.06	28.5	41.46	31.5
TUREF_3_Degree_GK_Zone_11	5271	Turkey - 31.5°E to 34.5°E onshore	35.97	31.5	42.07	34.5
TUREF_3_Degree_GK_Zone_12	5272	Turkey - 34.5°E to 37.5°E onshore	35.81	34.5	42.15	37.5
TUREF_3_Degree_GK_Zone_13	5273	Turkey - 37.5°E to 40.5°E onshore	36.66	37.5	41.19	40.5
TUREF_3_Degree_GK_Zone_14	5274	Turkey - 40.5°E to 43.5°E onshore	37.02	40.5	41.6	43.5
TUREF_3_Degree_GK_Zone_15	5275	Turkey - east of 43.5°E	36.97	43.5	41.02	44.83
TUREF_3_Degree_GK_Zone_9	5269	Turkey - west of 28.5°E onshore	36.5	25.62	42.11	28.5
TUREF_LAEA_Europe	5636	Turkey	34.42	25.62	43.45	44.83
TUREF_LCC_Europe	5637	Turkey	34.42	25.62	43.45	44.83
TUREF_TM27	5253	Turkey - west of 28.5°E onshore	36.5	25.62	42.11	28.5
TUREF_TM30	5254	Turkey - 28.5°E to 31.5°E onshore	36.06	28.5	41.46	31.5
TUREF_TM33	5255	Turkey - 31.5°E to 34.5°E onshore	35.97	31.5	42.07	34.5
TUREF_TM36	5256	Turkey - 34.5°E to 37.5°E onshore	35.81	34.5	42.15	37.5
TUREF_TM39	5257	Turkey - 37.5°E to 40.5°E onshore	36.66	37.5	41.19	40.5
TUREF_TM42	5258	Turkey - 40.5°E to 43.5°E onshore	37.02	40.5	41.6	43.5
TUREF_TM45	5259	Turkey - east of 43.5°E	36.97	43.5	41.02	44.83
TWD_1967_TM_Penghu	3827	Taiwan - onshore - Penghu	23.12	119.25	23.82	119.78
TWD_1967_TM_Taiwan	3828	Taiwan - onshore - mainland	21.87	119.99	25.34	122.06
TWD_1997_TM_Penghu	3825	Taiwan - 118°E to 120°E	18.63	118	24.65	120
TWD_1997_TM_Taiwan	3826	Taiwan - 120°E to 122°E	20.41	119.99	26.72	122.06
Ukraine_2000_3_Degree_GK_CM_21E	5577	Ukraine - west of 22.5°E	48.24	22.15	48.98	22.5
Ukraine_2000_3_Degree_GK_CM_24E	5578	Ukraine - 22.5°E to 25.5°E	47.71	22.5	51.96	25.5
Ukraine_2000_3_Degree_GK_CM_27E	5579	Ukraine - 25.5°E to 28.5°E	45.26	25.5	51.94	28.5
Ukraine_2000_3_Degree_GK_CM_30E	5580	Ukraine - 28.5°E to 31.5°E	43.42	28.5	52.12	31.5
Ukraine_2000_3_Degree_GK_CM_33E	5581	Ukraine - 31.5°E to 34.5°E	43.18	31.5	52.38	34.5
Ukraine_2000_3_Degree_GK_CM_36E	5582	Ukraine - 34.5°E to 37.5°E	43.24	34.5	51.25	37.5
Ukraine_2000_3_Degree_GK_CM_39E	5583	Ukraine - east of 37.5°E	46.77	37.5	50.39	40.18
Ukraine_2000_3_Degree_GK_Zone_10	5573	Ukraine - 28.5°E to 31.5°E	43.42	28.5	52.12	31.5
Ukraine_2000_3_Degree_GK_Zone_11	5574	Ukraine - 31.5°E to 34.5°E	43.18	31.5	52.38	34.5
Ukraine_2000_3_Degree_GK_Zone_12	5575	Ukraine - 34.5°E to 37.5°E	43.24	34.5	51.25	37.5
Ukraine_2000_3_Degree_GK_Zone_13	5576	Ukraine - east of 37.5°E	46.77	37.5	50.39	40.18
Ukraine_2000_3_Degree_GK_Zone_7	5570	Ukraine - west of 22.5°E	48.24	22.15	48.98	22.5
Ukraine_2000_3_Degree_GK_Zone_8	5571	Ukraine - 22.5°E to 25.5°E	47.71	22.5	51.96	25.5
Ukraine_2000_3_Degree_GK_Zone_9	5572	Ukraine - 25.5°E to 28.5°E	45.26	25.5	51.94	28.5
Ukraine_2000_GK_CM_21E	5566	Ukraine - west of 24°E	47.95	22.15	51.66	24
Ukraine_2000_GK_CM_27E	5567	Ukraine - 24°E to 30°E	45.1	24	51.96	30
Ukraine_2000_GK_CM_33E	5568	Ukraine - 30°E to 36°E	43.18	30	52.38	36
Ukraine_2000_GK_CM_39E	5569	Ukraine - east of 36°E	43.43	36	50.44	40.18
Ukraine_2000_GK_Zone_4	5562	Ukraine - west of 24°E	47.95	22.15	51.66	24
Ukraine_2000_GK_Zone_5	5563	Ukraine - 24°E to 30°E	45.1	24	51.96	30
Ukraine_2000_GK_Zone_6	5564	Ukraine - 30°E to 36°E	43.18	30	52.38	36
Ukraine_2000_GK_Zone_7	5565	Ukraine - east of 36°E	43.43	36	50.44	40.18
Ukraine_2000_TM_Zone_10	6384	Ukraine - 28.5°E to 31.5°E	43.42	28.5	52.12	31.5
Ukraine_2000_TM_Zone_11	6385	Ukraine - 31.5°E to 34.5°E	43.18	31.5	52.38	34.5
Ukraine_2000_TM_Zone_12	6386	Ukraine - 34.5°E to 37.5°E	43.24	34.5	51.25	37.5
Ukraine_2000_TM_Zone_13	6387	Ukraine - east of 37.5°E	46.77	37.5	50.39	40.18
Ukraine_2000_TM_Zone_7	6381	Ukraine - west of 22.5°E	48.24	22.15	48.98	22.5
Ukraine_2000_TM_Zone_8	6382	Ukraine - 22.5°E to 25.5°E	47.71	22.5	51.96	25.5
Ukraine_2000_TM_Zone_9	6383	Ukraine - 25.5°E to 28.5°E	45.26	25.5	51.94	28.5
UPS_North	32661	World - N hemisphere - north of 60°N	60	-180	90	180
UPS_South	32761	World - S hemisphere - south of 60°S	-90	-180	-60	180
USA_Contiguous_Albers_Equal_Area_ Conic	102003	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
USA_Contiguous_Albers_Equal_Area_ Conic_USGS_version	102039	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
USA_Contiguous_Equidistant_Conic	102005	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
USA_Contiguous_Lambert_Conformal_ Conic	102004	USA - CONUS - onshore	24.41	-124.79	49.38	-66.91
US_National_Atlas_Equal_Area	2163	USA	15.56	167.65	74.71	-65.69
UTM_Bangladesh_(BTM)	102953	Bangladesh	18.56	88.01	26.64	92.67
UTM_Gulshan	102955	Bangladesh	18.56	88.01	26.64	92.67
UWPP_1992	102194	Poland	49	14.14	55.93	24.15
UWPP_2000_PAS_5	102195	Poland - west of 16.5°E	50.26	14.14	55.35	16.5
UWPP_2000_PAS_6	102196	Poland - 16.5°E to 19.5°E	49.39	16.5	55.93	19.5
UWPP_2000_PAS_7	102197	Poland - 19.5°E to 22.5°E	49.09	19.5	54.55	22.5
UWPP_2000_PAS_8	102198	Poland - east of 22.5°E	49	22.5	54.41	24.15
VN-2000_TM-3_103-00	9205	Vietnam - Dien Bien and Lai Chau	20.89	102.14	22.82	103.99
VN-2000_TM-3_104-00	9206	Vietnam - Son La	20.57	103.21	22.04	105.03
VN-2000_TM-3_104-30	9207	Vietnam - Ca Mau and Kien Giang	8.33	103.4	10.55	105.54
VN-2000_TM-3_104-45	9208	Vietnam - An Giang, Lao Cai, Nghe An, Phu Tho, Yen Bai	10.18	103.53	22.85	105.86
VN-2000_TM-3_105-30	9209	Vietnam - 104°20'E to 106°40'E by province	9.19	104.33	23.4	106.69
VN-2000_TM-3_105-45	9210	Vietnam - 105°15'E to 107°50'E by province - HCMC	9.75	105.26	23.12	107.8
VN-2000_TM-3_106-00	9211	Vietnam - Hoa Binh, Quang Binh and Tuyen Quang	16.92	104.83	22.7	107.03
VN-2000_TM-3_106-15	9212	Vietnam - Binh Phuoc and Quang Tri	11.3	106.41	17.22	107.43
VN-2000_TM-3_106-30	9213	Vietnam - Bac Kan and Thai Nguyen	21.32	105.43	22.75	106.25
VN-2000_TM-3_107-00	9214	Vietnam - Bac Giang and Thua Thien-Hue	15.99	105.88	21.63	108.24
VN-2000_TM-3_107-15	9215	Vietnam - Lang Son	21.32	106.09	22.47	107.37
VN-2000_TM-3_107-30	9216	Vietnam - Kon Tum	13.92	107.33	15.42	108.55
VN_2000_TM-3_107-45	5899	Vietnam - Quang Ninh; Da Nang, Quang Nam; Ba Ria-Vung Tau, Dong Nai, Lam Dong	8.57	106.43	21.67	108.76
VN-2000_TM-3_108-15	9217	Vietnam - Binh Dinh, Khanh Hoa, Ninh Thuan	11.25	108.55	14.71	109.53
VN-2000_TM-3_108-30	9218	Vietnam - Binh Thuan, Dak Lak, Dak Nong, Gia Lai, Phu Yen	10.43	107.2	14.61	109.52
VN_2000_TM-3_zone_481	5896	Vietnam - west of 103°30'E onshore	9.2	102.14	22.82	103.51
VN_2000_TM-3_zone_482	5897	Vietnam - 103.5°E to 106.5°E onshore	8.33	103.5	23.4	106.51
VN_2000_TM-3_zone_491	5898	Vietnam - east of 106.5°E onshore	8.57	106.5	22.95	109.53
VN_2000_UTM_Zone_48N	3405	Vietnam - west of 108°E onshore	8.33	102.14	23.4	108
VN_2000_UTM_Zone_49N	3406	Vietnam - east of 108°E onshore	10.43	108	21.56	109.53
Voirol_1879_Nord_Algerie_Ancienne	30493	Algeria - north of 34°39'N	34.64	-2.22	37.14	8.64
Voirol_1879_Sud_Algerie_Ancienne	30494	Algeria - 31°30'N to 34°39'N	31.49	-3.85	34.66	9.22
WGS_1972_BE_South_China_Sea_ Lambert	3415	China - offshore - Pearl River basin	18.31	110.13	22.89	116.76
WGS_1972_BE_TM_106_NE	2094	Vietnam - offshore Cuu Long basin	7.99	106.54	11.15	110
WGS_1972_UTM_Zone_10N	32210	World - N hemisphere - 126°W to 120°W	0	-126	84	-120
WGS_1972_UTM_Zone_10S	32310	World - S hemisphere - 126°W to 120°W	-80	-126	0	-120
WGS_1972_UTM_Zone_11N	32211	World - N hemisphere - 120°W to 114°W	0	-120	84	-114
WGS_1972_UTM_Zone_11S	32311	World - S hemisphere - 120°W to 114°W	-80	-120	0	-114
WGS_1972_UTM_Zone_12N	32212	World - N hemisphere - 114°W to 108°W	0	-114	84	-108
WGS_1972_UTM_Zone_12S	32312	World - S hemisphere - 114°W to 108°W	-80	-114	0	-108
WGS_1972_UTM_Zone_13N	32213	World - N hemisphere - 108°W to 102°W	0	-108	84	-102
WGS_1972_UTM_Zone_13S	32313	World - S hemisphere - 108°W to 102°W	-80	-108	0	-102
WGS_1972_UTM_Zone_14N	32214	World - N hemisphere - 102°W to 96°W	0	-102	84	-96
WGS_1972_UTM_Zone_14S	32314	World - S hemisphere - 102°W to 96°W	-80	-102	0	-96
WGS_1972_UTM_Zone_15N	32215	World - N hemisphere - 96°W to 90°W	0	-96	84	-90
WGS_1972_UTM_Zone_15S	32315	World - S hemisphere - 96°W to 90°W	-80	-96	0	-90
WGS_1972_UTM_Zone_16N	32216	World - N hemisphere - 90°W to 84°W	0	-90	84	-84
WGS_1972_UTM_Zone_16S	32316	World - S hemisphere - 90°W to 84°W	-80	-90	0	-84
WGS_1972_UTM_Zone_17N	32217	World - N hemisphere - 84°W to 78°W	0	-84	84	-78
WGS_1972_UTM_Zone_17S	32317	World - S hemisphere - 84°W to 78°W	-80	-84	0	-78
WGS_1972_UTM_Zone_18N	32218	World - N hemisphere - 78°W to 72°W	0	-78	84	-72
WGS_1972_UTM_Zone_18S	32318	World - S hemisphere - 78°W to 72°W	-80	-78	0	-72
WGS_1972_UTM_Zone_19N	32219	World - N hemisphere - 72°W to 66°W	0	-72	84	-66
WGS_1972_UTM_Zone_19S	32319	World - S hemisphere - 72°W to 66°W	-80	-72	0	-66
WGS_1972_UTM_Zone_1N	32201	World - N hemisphere - 180°W to 174°W	0	-180	84	-174
WGS_1972_UTM_Zone_1S	32301	World - S hemisphere - 180°W to 174°W	-80	-180	0	-174
WGS_1972_UTM_Zone_20N	32220	World - N hemisphere - 66°W to 60°W	0	-66	84	-60
WGS_1972_UTM_Zone_20S	32320	World - S hemisphere - 66°W to 60°W	-80	-66	0	-60
WGS_1972_UTM_Zone_21N	32221	World - N hemisphere - 60°W to 54°W	0	-60	84	-54
WGS_1972_UTM_Zone_21S	32321	World - S hemisphere - 60°W to 54°W	-80	-60	0	-54
WGS_1972_UTM_Zone_22N	32222	World - N hemisphere - 54°W to 48°W	0	-54	84	-48
WGS_1972_UTM_Zone_22S	32322	World - S hemisphere - 54°W to 48°W	-80	-54	0	-48
WGS_1972_UTM_Zone_23N	32223	World - N hemisphere - 48°W to 42°W	0	-48	84	-42
WGS_1972_UTM_Zone_23S	32323	World - S hemisphere - 48°W to 42°W	-80	-48	0	-42
WGS_1972_UTM_Zone_24N	32224	World - N hemisphere - 42°W to 36°W	0	-42	84	-36
WGS_1972_UTM_Zone_24S	32324	World - S hemisphere - 42°W to 36°W	-80	-42	0	-36
WGS_1972_UTM_Zone_25N	32225	World - N hemisphere - 36°W to 30°W	0	-36	84	-30
WGS_1972_UTM_Zone_25S	32325	World - S hemisphere - 36°W to 30°W	-80	-36	0	-30
WGS_1972_UTM_Zone_26N	32226	World - N hemisphere - 30°W to 24°W	0	-30	84	-24
WGS_1972_UTM_Zone_26S	32326	World - S hemisphere - 30°W to 24°W	-80	-30	0	-24
WGS_1972_UTM_Zone_27N	32227	World - N hemisphere - 24°W to 18°W	0	-24	84	-18
WGS_1972_UTM_Zone_27S	32327	World - S hemisphere - 24°W to 18°W	-80	-24	0	-18
WGS_1972_UTM_Zone_28N	32228	World - N hemisphere - 18°W to 12°W	0	-18	84	-12
WGS_1972_UTM_Zone_28S	32328	World - S hemisphere - 18°W to 12°W	-80	-18	0	-12
WGS_1972_UTM_Zone_29N	32229	World - N hemisphere - 12°W to 6°W	0	-12	84	-6
WGS_1972_UTM_Zone_29S	32329	World - S hemisphere - 12°W to 6°W	-80	-12	0	-6
WGS_1972_UTM_Zone_2N	32202	World - N hemisphere - 174°W to 168°W	0	-174	84	-168
WGS_1972_UTM_Zone_2S	32302	World - S hemisphere - 174°W to 168°W	-80	-174	0	-168
WGS_1972_UTM_Zone_30N	32230	World - N hemisphere - 6°W to 0°W	0	-6	84	0
WGS_1972_UTM_Zone_30S	32330	World - S hemisphere - 6°W to 0°W	-80	-6	0	0
WGS_1972_UTM_Zone_31N	32231	World - N hemisphere - 0°E to 6°E	0	0	84	6
WGS_1972_UTM_Zone_31S	32331	World - S hemisphere - 0°E to 6°E	-80	0	0	6
WGS_1972_UTM_Zone_32N	32232	World - N hemisphere - 6°E to 12°E	0	6	84	12
WGS_1972_UTM_Zone_32S	32332	World - S hemisphere - 6°E to 12°E	-80	6	0	12
WGS_1972_UTM_Zone_33N	32233	World - N hemisphere - 12°E to 18°E	0	12	84	18
WGS_1972_UTM_Zone_33S	32333	World - S hemisphere - 12°E to 18°E	-80	12	0	18
WGS_1972_UTM_Zone_34N	32234	World - N hemisphere - 18°E to 24°E	0	18	84	24
WGS_1972_UTM_Zone_34S	32334	World - S hemisphere - 18°E to 24°E	-80	18	0	24
WGS_1972_UTM_Zone_35N	32235	World - N hemisphere - 24°E to 30°E	0	24	84	30
WGS_1972_UTM_Zone_35S	32335	World - S hemisphere - 24°E to 30°E	-80	24	0	30
WGS_1972_UTM_Zone_36N	32236	World - N hemisphere - 30°E to 36°E	0	30	84	36
WGS_1972_UTM_Zone_36S	32336	World - S hemisphere - 30°E to 36°E	-80	30	0	36
WGS_1972_UTM_Zone_37N	32237	World - N hemisphere - 36°E to 42°E	0	36	84	42
WGS_1972_UTM_Zone_37S	32337	World - S hemisphere - 36°E to 42°E	-80	36	0	42
WGS_1972_UTM_Zone_38N	32238	World - N hemisphere - 42°E to 48°E	0	42	84	48
WGS_1972_UTM_Zone_38S	32338	World - S hemisphere - 42°E to 48°E	-80	42	0	48
WGS_1972_UTM_Zone_39N	32239	World - N hemisphere - 48°E to 54°E	0	48	84	54
WGS_1972_UTM_Zone_39S	32339	World - S hemisphere - 48°E to 54°E	-80	48	0	54
WGS_1972_UTM_Zone_3N	32203	World - N hemisphere - 168°W to 162°W	0	-168	84	-162
WGS_1972_UTM_Zone_3S	32303	World - S hemisphere - 168°W to 162°W	-80	-168	0	-162
WGS_1972_UTM_Zone_40N	32240	World - N hemisphere - 54°E to 60°E	0	54	84	60
WGS_1972_UTM_Zone_40S	32340	World - S hemisphere - 54°E to 60°E	-80	54	0	60
WGS_1972_UTM_Zone_41N	32241	World - N hemisphere - 60°E to 66°E	0	60	84	66
WGS_1972_UTM_Zone_41S	32341	World - S hemisphere - 60°E to 66°E	-80	60	0	66
WGS_1972_UTM_Zone_42N	32242	World - N hemisphere - 66°E to 72°E	0	66	84	72
WGS_1972_UTM_Zone_42S	32342	World - S hemisphere - 66°E to 72°E	-80	66	0	72
WGS_1972_UTM_Zone_43N	32243	World - N hemisphere - 72°E to 78°E	0	72	84	78
WGS_1972_UTM_Zone_43S	32343	World - S hemisphere - 72°E to 78°E	-80	72	0	78
WGS_1972_UTM_Zone_44N	32244	World - N hemisphere - 78°E to 84°E	0	78	84	84
WGS_1972_UTM_Zone_44S	32344	World - S hemisphere - 78°E to 84°E	-80	78	0	84
WGS_1972_UTM_Zone_45N	32245	World - N hemisphere - 84°E to 90°E	0	84	84	90
WGS_1972_UTM_Zone_45S	32345	World - S hemisphere - 84°E to 90°E	-80	84	0	90
WGS_1972_UTM_Zone_46N	32246	World - N hemisphere - 90°E to 96°E	0	90	84	96
WGS_1972_UTM_Zone_46S	32346	World - S hemisphere - 90°E to 96°E	-80	90	0	96
WGS_1972_UTM_Zone_47N	32247	World - N hemisphere - 96°E to 102°E	0	96	84	102
WGS_1972_UTM_Zone_47S	32347	World - S hemisphere - 96°E to 102°E	-80	96	0	102
WGS_1972_UTM_Zone_48N	32248	World - N hemisphere - 102°E to 108°E	0	102	84	108
WGS_1972_UTM_Zone_48S	32348	World - S hemisphere - 102°E to 108°E	-80	102	0	108
WGS_1972_UTM_Zone_49N	32249	World - N hemisphere - 108°E to 114°E	0	108	84	114
WGS_1972_UTM_Zone_49S	32349	World - S hemisphere - 108°E to 114°E	-80	108	0	114
WGS_1972_UTM_Zone_4N	32204	World - N hemisphere - 162°W to 156°W	0	-162	84	-156
WGS_1972_UTM_Zone_4S	32304	World - S hemisphere - 162°W to 156°W	-80	-162	0	-156
WGS_1972_UTM_Zone_50N	32250	World - N hemisphere - 114°E to 120°E	0	114	84	120
WGS_1972_UTM_Zone_50S	32350	World - S hemisphere - 114°E to 120°E	-80	114	0	120
WGS_1972_UTM_Zone_51N	32251	World - N hemisphere - 120°E to 126°E	0	120	84	126
WGS_1972_UTM_Zone_51S	32351	World - S hemisphere - 120°E to 126°E	-80	120	0	126
WGS_1972_UTM_Zone_52N	32252	World - N hemisphere - 126°E to 132°E	0	126	84	132
WGS_1972_UTM_Zone_52S	32352	World - S hemisphere - 126°E to 132°E	-80	126	0	132
WGS_1972_UTM_Zone_53N	32253	World - N hemisphere - 132°E to 138°E	0	132	84	138
WGS_1972_UTM_Zone_53S	32353	World - S hemisphere - 132°E to 138°E	-80	132	0	138
WGS_1972_UTM_Zone_54N	32254	World - N hemisphere - 138°E to 144°E	0	138	84	144
WGS_1972_UTM_Zone_54S	32354	World - S hemisphere - 138°E to 144°E	-80	138	0	144
WGS_1972_UTM_Zone_55N	32255	World - N hemisphere - 144°E to 150°E	0	144	84	150
WGS_1972_UTM_Zone_55S	32355	World - S hemisphere - 144°E to 150°E	-80	144	0	150
WGS_1972_UTM_Zone_56N	32256	World - N hemisphere - 150°E to 156°E	0	150	84	156
WGS_1972_UTM_Zone_56S	32356	World - S hemisphere - 150°E to 156°E	-80	150	0	156
WGS_1972_UTM_Zone_57N	32257	World - N hemisphere - 156°E to 162°E	0	156	84	162
WGS_1972_UTM_Zone_57S	32357	World - S hemisphere - 156°E to 162°E	-80	156	0	162
WGS_1972_UTM_Zone_58N	32258	World - N hemisphere - 162°E to 168°E	0	162	84	168
WGS_1972_UTM_Zone_58S	32358	World - S hemisphere - 162°E to 168°E	-80	162	0	168
WGS_1972_UTM_Zone_59N	32259	World - N hemisphere - 168°E to 174°E	0	168	84	174
WGS_1972_UTM_Zone_59S	32359	World - S hemisphere - 168°E to 174°E	-80	168	0	174
WGS_1972_UTM_Zone_5N	32205	World - N hemisphere - 156°W to 150°W	0	-156	84	-150
WGS_1972_UTM_Zone_5S	32305	World - S hemisphere - 156°W to 150°W	-80	-156	0	-150
WGS_1972_UTM_Zone_60N	32260	World - N hemisphere - 174°E to 180°E	0	174	84	180
WGS_1972_UTM_Zone_60S	32360	World - S hemisphere - 174°E to 180°E	-80	174	0	180
WGS_1972_UTM_Zone_6N	32206	World - N hemisphere - 150°W to 144°W	0	-150	84	-144
WGS_1972_UTM_Zone_6S	32306	World - S hemisphere - 150°W to 144°W	-80	-150	0	-144
WGS_1972_UTM_Zone_7N	32207	World - N hemisphere - 144°W to 138°W	0	-144	84	-138
WGS_1972_UTM_Zone_7S	32307	World - S hemisphere - 144°W to 138°W	-80	-144	0	-138
WGS_1972_UTM_Zone_8N	32208	World - N hemisphere - 138°W to 132°W	0	-138	84	-132
WGS_1972_UTM_Zone_8S	32308	World - S hemisphere - 138°W to 132°W	-80	-138	0	-132
WGS_1972_UTM_Zone_9N	32209	World - N hemisphere - 132°W to 126°W	0	-132	84	-126
WGS_1972_UTM_Zone_9S	32309	World - S hemisphere - 132°W to 126°W	-80	-132	0	-126
WGS_1984_Adams_Square_II	54098	World	-90	-180	90	180
WGS_1984_Andaman_and_Nicobar_ Islands	7777	India - Andaman and Nicobar Islands	6.7	92.15	13.73	94.33
WGS_1984_Andhra_Pradesh	7756	India - Andhra Pradesh and Telangana	12.61	76.75	19.92	84.81
WGS_1984_Antarctic_Polar_ Stereographic	3031	Antarctica	-90	-180	-60	180
WGS_1984_ARC_System_Zone_01	102421	ARC System - Zone 1	0	-180	32	180
WGS_1984_ARC_System_Zone_02	102422	ARC System - Zone 2	32	-180	48	180
WGS_1984_ARC_System_Zone_03	102423	ARC System - Zone 3	48	-180	56	180
WGS_1984_ARC_System_Zone_04	102424	ARC System - Zone 4	56	-180	64	180
WGS_1984_ARC_System_Zone_05	102425	ARC System - Zone 5	64	-180	68	180
WGS_1984_ARC_System_Zone_06	102426	ARC System - Zone 6	68	-180	72	180
WGS_1984_ARC_System_Zone_07	102427	ARC System - Zone 7	72	-180	76	180
WGS_1984_ARC_System_Zone_08	102428	ARC System - Zone 8	76	-180	80	180
WGS_1984_ARC_System_Zone_09	102429	ARC System - Zone 9	80	-180	90	180
WGS_1984_ARC_System_Zone_10	102430	ARC System - Zone 10	-32	-180	0	180
WGS_1984_ARC_System_Zone_11	102431	ARC System - Zone 11	-48	-180	-32	180
WGS_1984_ARC_System_Zone_12	102432	ARC System - Zone 12	-56	-180	-48	180
WGS_1984_ARC_System_Zone_13	102433	ARC System - Zone 13	-64	-180	-56	180
WGS_1984_ARC_System_Zone_14	102434	ARC System - Zone 14	-68	-180	-64	180
WGS_1984_ARC_System_Zone_15	102435	ARC System - Zone 15	-72	-180	-68	180
WGS_1984_ARC_System_Zone_16	102436	ARC System - Zone 16	-76	-180	-72	180
WGS_1984_ARC_System_Zone_17	102437	ARC System - Zone 17	-80	-180	-76	180
WGS_1984_ARC_System_Zone_18	102438	ARC System - Zone 18	-90	-180	-80	180
WGS_1984_Arctic_Polar_Stereographic	3995	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_Arunachal_Pradesh	7757	India - Arunachal Pradesh	26.65	91.55	29.47	97.42
WGS_1984_Assam	7758	India - Assam	24.13	89.69	27.98	96.03
WGS_1984_Australian_Antarctic_ Lambert	3033	Antarctica - Australian sector north of 80°S	-80	45	-60	160
WGS_1984_Australian_Antarctic_Polar_ Stereographic	3032	Antarctica - Australian sector	-90	45	-60	160
WGS_1984_Australian_Centre_for_ Remote_Sensing_Lambert	4462	Australia - onshore	-43.7	112.85	-9.86	153.69
WGS_1984_Bihar	7759	India - Bihar	24.28	83.31	27.86	88.3
WGS_1984_BLM_Zone_14N_ftUS	32664	USA - GoM OCS - west of 96°W	25.97	-97.22	28.43	-95.87
WGS_1984_BLM_Zone_15N_ftUS	32665	USA - GoM OCS - 96°W to 90°W	25.61	-96	29.73	-89.86
WGS_1984_BLM_Zone_16N_ftUS	32666	USA - GoM OCS - 90°W to 84°W	23.95	-90.01	30.25	-83.91
WGS_1984_BLM_Zone_17N_ftUS	32667	USA - GoM OCS - east of 84°W	23.82	-84.09	29.94	-81.17
WGS_1984_California_Teale_Albers_Ft_I ntl	102759	USA - California	32.53	-124.45	42.01	-114.12
WGS_1984_California_Teale_Albers_FtUS	102599	USA - California	32.53	-124.45	42.01	-114.12
WGS_1984_Canada_Atlas_LCC	102215	Canada	38.21	-141.01	86.46	-40.73
WGS_1984_Cape_Verde_Grid	4826	Cape Verde	11.47	-28.85	20.54	-19.53
WGS_1984_Chhattisgarh	7778	India - Chhattisgarh	17.78	80.23	24.11	84.39
WGS_1984_CIG92	6720	Christmas Island - onshore	-10.63	105.48	-10.36	105.77
WGS_1984_CKIG92	6722	Cocos (Keeling) Islands - onshore	-12.27	96.76	-11.76	96.99
WGS_1984_Complex_UTM_Zone_20N	102570	World - N hemisphere - 66°W to 60°W	0	-66	84	-60
WGS_1984_Complex_UTM_Zone_21N	102571	World - N hemisphere - 60°W to 54°W	0	-60	84	-54
WGS_1984_Complex_UTM_Zone_22N	102572	World - N hemisphere - 54°W to 48°W	0	-54	84	-48
WGS_1984_Complex_UTM_Zone_23N	102573	World - N hemisphere - 48°W to 42°W	0	-48	84	-42
WGS_1984_Complex_UTM_Zone_24N	102574	World - N hemisphere - 42°W to 36°W	0	-42	84	-36
WGS_1984_Complex_UTM_Zone_25N	102575	World - N hemisphere - 36°W to 30°W	0	-36	84	-30
WGS_1984_Complex_UTM_Zone_26N	102576	World - N hemisphere - 30°W to 24°W	0	-30	84	-24
WGS_1984_Complex_UTM_Zone_27N	102577	World - N hemisphere - 24°W to 18°W	0	-24	84	-18
WGS_1984_Complex_UTM_Zone_28N	102578	World - N hemisphere - 18°W to 12°W	0	-18	84	-12
WGS_1984_Complex_UTM_Zone_29N	102579	World - N hemisphere - 12°W to 6°W	0	-12	84	-6
WGS_1984_Complex_UTM_Zone_30N	102580	World - N hemisphere - 6°W to 0°W	0	-6	84	0
WGS_1984_Costa_Rica_TM_90	102223	Costa Rica	2.15	-90.45	11.77	-81.43
WGS_1984_Delhi	7760	India - Delhi	28.4	76.83	28.89	77.34
WGS_1984_Dubai_Local_TM	3997	UAE - Dubai municipality	24.85	54.84	25.34	55.55
WGS_1984_EASE-Grid_2.0_Global	6933	World - 86°S to 86°N	-86	-180	86	180
WGS_1984_EASE-Grid_2.0_North	6931	World - north of 0°N	0	-180	90	180
WGS_1984_EASE-Grid_2.0_South	6932	World - south of 0°N	-90	-180	0	180
WGS_1984_EASE_Grid_Global	3975	World - 86°S to 86°N	-86	-180	86	180
WGS_1984_EASE_Grid_North	3973	World - north of 0°N	0	-180	90	180
WGS_1984_EASE_Grid_South	3974	World - south of 0°N	-90	-180	0	180
WGS_1984_EPSG_Alaska_Polar_ Stereographic	5936	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_EPSG_Arctic_Regional_zone_ A1	5921	Arctic - 87°N to 75°N, 156°W to 66°W	75	-156	87.01	-66
WGS_1984_EPSG_Arctic_Regional_zone_ A2	5922	Arctic - 87°N to 75°N, 84°W to 6°E	75	-84	87.01	6.01
WGS_1984_EPSG_Arctic_Regional_zone_ A3	5923	Arctic - 87°N to 75°N, 12°W to 78°E	75	-12	87.01	78.01
WGS_1984_EPSG_Arctic_Regional_zone_ A4	5924	Arctic - 87°N to 75°N, 60°E to 150°E	75	60	87.01	150.01
WGS_1984_EPSG_Arctic_Regional_zone_ A5	5925	Arctic - 87°N to 75°N, 132°E to 138°W	75	132	87.01	-138
WGS_1984_EPSG_Arctic_Regional_zone_ B1	5926	Arctic - 79°N to 67°N, 156°W to 66°W	67	-156	79.01	-66
WGS_1984_EPSG_Arctic_Regional_zone_ B2	5927	Arctic - 79°N to 67°N, 84°W to 6°E	67	-84	79.01	6.01
WGS_1984_EPSG_Arctic_Regional_zone_ B3	5928	Arctic - 79°N to 67°N, 12°W to 78°E	67	-12	79.01	78.01
WGS_1984_EPSG_Arctic_Regional_zone_ B4	5929	Arctic - 79°N to 67°N, 60°E to 150°E	67	60	79.01	150.01
WGS_1984_EPSG_Arctic_Regional_zone_ B5	5930	Arctic - 79°N to 67°N, 132°E to 138°W	67	132	79.01	-138
WGS_1984_EPSG_Arctic_Regional_zone_ C1	5931	Arctic - 71°N to 59°N, 156°W to 66°W	59	-156	71	-66
WGS_1984_EPSG_Arctic_Regional_zone_ C2	5932	Arctic - 71°N to 59°N, 84°W to 6°E	59	-84	71	6
WGS_1984_EPSG_Arctic_Regional_zone_ C3	5933	Arctic - 71°N to 59°N, 12°W to 78°E	59	-12	71	78.01
WGS_1984_EPSG_Arctic_Regional_zone_ C4	5934	Arctic - 71°N to 59°N, 60°E to 150°E	59	60	71	150.01
WGS_1984_EPSG_Arctic_Regional_zone_ C5	5935	Arctic - 71°N to 59°N, 132°E to 138°W	59	132	71	-138
WGS_1984_EPSG_Arctic_zone_1-21	6118	Arctic - 87°50'N to 82°50'N, 180°W to 120°W	82.83	-180	87.84	-120
WGS_1984_EPSG_Arctic_zone_1-27	6115	Arctic - 87°50'N to 82°50'N, 0°E to 60°E	82.83	0	87.84	60.01
WGS_1984_EPSG_Arctic_zone_1-29	6116	Arctic - 87°50'N to 82°50'N, 60°E to 120°E	82.83	60	87.84	120.01
WGS_1984_EPSG_Arctic_zone_1-31	6117	Arctic - 87°50'N to 82°50'N, 120°E to 180°E	82.83	120	87.83	180
WGS_1984_EPSG_Arctic_zone_2-10	6120	Arctic - 84°30'N to 79°30'N, 146°E to 174°W	79.5	146	84.51	-173.99
WGS_1984_EPSG_Arctic_zone_2-12	6121	Arctic - 84°30'N to 79°30'N, 174°W to 135°W	79.5	-174	84.51	-134.99
WGS_1984_EPSG_Arctic_zone_2-24	6075	Arctic - 84°30'N to 79°30'N, 33°E to 73°E	79.5	33	84.51	73.01
WGS_1984_EPSG_Arctic_zone_2-26	6076	Arctic - 84°30'N to 79°30'N, 73°E to 113°E	79.5	73	84.51	113.01
WGS_1984_EPSG_Arctic_zone_2-28	6119	Arctic - 84°30'N to 79°30'N, 113°E to 153°E	79.5	113	84.51	153.01
WGS_1984_EPSG_Arctic_zone_3-13	6077	Arctic - 81°10'N to 76°10'N, 35°E to 67°E	76.16	34.99	81.17	67.01
WGS_1984_EPSG_Arctic_zone_3-15	6078	Arctic - 81°10'N to 76°10'N, 67°E to 98°E	76.16	67	81.17	98.01
WGS_1984_EPSG_Arctic_zone_3-17	6079	Arctic - 81°10'N to 76°10'N, 98°E to 129°E	76.16	98	81.17	129.01
WGS_1984_EPSG_Arctic_zone_3-19	6080	Arctic - 81°10'N to 76°10'N, 129°E to 160°E	76.16	129	81.17	160.01
WGS_1984_EPSG_Arctic_zone_3-21	6122	Arctic - 81°10'N to 76°10'N, 160°E to 169°W	76.16	160	81.17	-168.99
WGS_1984_EPSG_Arctic_zone_3-23	6123	Arctic - 81°10'N to 76°10'N, 169°W to 138°W	76.16	-169	81.17	-138
WGS_1984_EPSG_Arctic_zone_4-12	6124	Arctic - 77°50'N to 72°50'N, 169°W to 141°W	72.83	-169	77.84	-141
WGS_1984_EPSG_Arctic_zone_4-30	6081	Arctic - 77°50'N to 72°50'N, 46°E to 70°E	72.83	46	77.84	70.01
WGS_1984_EPSG_Arctic_zone_4-32	6082	Arctic - 77°50'N to 72°50'N, 70°E to 94°E	72.83	70	77.84	94.01
WGS_1984_EPSG_Arctic_zone_4-34	6083	Arctic - 77°50'N to 72°50'N, 94°E to 118°E	72.83	94	77.84	118.01
WGS_1984_EPSG_Arctic_zone_4-36	6084	Arctic - 77°50'N to 72°50'N, 118°E to 142°E	72.83	118	77.84	142.01
WGS_1984_EPSG_Arctic_zone_4-38	6085	Arctic - 77°50'N to 72°50'N, 142°E to 166°E	72.83	142	77.84	166.01
WGS_1984_EPSG_Arctic_zone_4-40	6086	Arctic - 77°50'N to 72°50'N, 166°E to 169°W	72.83	166	77.84	-168.99
WGS_1984_EPSG_Arctic_zone_5-15	6087	Arctic - 74°30'N to 69°30'N, 44°E to 64°E	69.5	44	74.51	64.01
WGS_1984_EPSG_Arctic_zone_5-17	6088	Arctic - 74°30'N to 69°30'N, 64°E to 85°E	69.5	64	74.51	85.01
WGS_1984_EPSG_Arctic_zone_5-19	6089	Arctic - 74°30'N to 69°30'N, 85°E to 106°E	69.5	85	74.51	106.01
WGS_1984_EPSG_Arctic_zone_5-21	6090	Arctic - 74°30'N to 69°30'N, 106°E to 127°E	69.5	106	74.51	127.01
WGS_1984_EPSG_Arctic_zone_5-23	6091	Arctic - 74°30'N to 69°30'N, 127°E to 148°E	69.5	127	74.51	148
WGS_1984_EPSG_Arctic_zone_5-25	6092	Arctic - 74°30'N to 69°30'N, 148°E to 169°E	69.5	148	74.51	169.01
WGS_1984_EPSG_Arctic_zone_5-27	6093	Arctic - 74°30'N to 69°30'N, 169°E to 169°W	69.5	169	74.51	-169
WGS_1984_EPSG_Canada_Polar_ Stereographic	5937	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_EPSG_Greenland_Polar_ Stereographic	5938	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_EPSG_Norway_Polar_ Stereographic	5939	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_EPSG_Russia_Polar_ Stereographic	5940	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_Equal_Earth_Greenwich	8857	World	-90	-180	90	180
WGS_1984_Equal_Earth_Americas	8858	World	-90	-180	90	180
WGS_1984_Equal_Earth_Asia_Pacific	8859	World	-90	-180	90	180
WGS_1984_Goa	7779	India - Goa	14.86	73.61	15.8	74.35
WGS_1984_Gujarat	7761	India - Gujarat	20.05	68.13	24.71	74.48
WGS_1984_Haryana	7762	India - Haryana	27.65	74.46	30.94	77.6
WGS_1984_Himachal_Pradesh	7763	India - Himachal Pradesh	30.38	75.57	33.26	79
WGS_1984_IBCAO_Polar_Stereographic	3996	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_India_Northeast	7771	India - northeast	21.94	89.69	29.47	97.42
WGS_1984_India_NSF_LCC	7755	India	3.87	65.6	35.51	97.42
WGS_1984_Jammu_and_Kashmir	7764	India - Jammu and Kashmir	32.27	73.76	35.51	79.57
WGS_1984_Jharkhand	7765	India - Jharkhand	21.96	83.32	25.35	87.98
WGS_1984_Karnataka	7780	India - Karnataka	11.57	74	18.46	78.58
WGS_1984_Kerala	7781	India - Kerala	8.25	74.81	12.8	77.4
WGS_1984_Lakshadweep	7782	India - Lakshadweep	8.21	72.04	11.76	73.76
WGS_1984_Madhya_Pradesh	7766	India - Madhya Pradesh	21.07	74.03	26.88	82.81
WGS_1984_Maharashtra	7767	India - Maharashtra	15.6	72.6	22.04	80.9
WGS_1984_Manipur	7768	India - Manipur	23.84	92.97	25.7	94.76
WGS_1984_Meghalaya	7769	India - Meghalaya	25.03	89.82	26.12	92.81
WGS_1984_Mercator_41	3994	New Zealand - offshore Pacific Ocean, Southern Ocean	-60	155	-25	-170
WGS_1984_Mizoram	7783	India - Mizoram	21.94	92.25	24.53	93.45
WGS_1984_Nagaland	7770	India - Nagaland	25.2	93.33	27.05	95.25
WGS_1984_NIWA_Albers	9191	New Zealand - offshore Pacific Ocean, Southern Ocean	-60	155	-25	-170
WGS_1984_North_Pole_LAEA_Alaska	3572	World - north of 45°N	45	-180	90	180
WGS_1984_North_Pole_LAEA_Atlantic	3574	World - north of 45°N	45	-180	90	180
WGS_1984_North_Pole_LAEA_Bering_ Sea	3571	World - north of 45°N	45	-180	90	180
WGS_1984_North_Pole_LAEA_Canada	3573	World - north of 45°N	45	-180	90	180
WGS_1984_North_Pole_LAEA_Europe	3575	World - north of 45°N	45	-180	90	180
WGS_1984_North_Pole_LAEA_Russia	3576	World - north of 45°N	45	-180	90	180
WGS_1984_NSIDC_Sea_Ice_Polar_ Stereographic_North	3413	World - N hemisphere - north of 60°N	60	-180	90	180
WGS_1984_NSIDC_Sea_Ice_Polar_ Stereographic_South	3976	World - S hemisphere - south of 60°S	-90	-180	-60	180
WGS_1984_Orissa	7772	India - Odisha	17.8	81.38	22.57	87.5
WGS_1984_PDC_Mercator	3832	Pacific Ocean	-60	98.69	66.67	-68
WGS_1984_Peirce_quincuncial_North_ Pole_diamond	54091	World	-90	-180	90	180
WGS_1984_Peirce_quincuncial_North_ Pole_square	54090	World	-90	-180	90	180
WGS_1984_Plate_Carree	32662	World	-90	-180	90	180
WGS_1984_Punjab	7773	India - Punjab	29.54	73.87	32.58	76.94
WGS_1984_Rajasthan	7774	India - Rajasthan	23.06	69.48	30.2	78.27
WGS_1984_Sikkim	7784	India - Sikkim	27.08	88.01	28.14	88.92
WGS_1984_South_Georgia_Lambert	3762	South Georgia - onshore	-54.95	-38.08	-53.93	-35.74
WGS_1984_Spilhaus_Ocean_Map_in_ Square	54099	World	-90	-180	90	180
WGS_1984_Tamil_Nadu	7785	India - Tamil Nadu	8.02	76.22	13.59	80.4
WGS_1984_TM_116_SE	2309	Indonesia - Bali Sea west	-8.46	112.8	-6.8	117.01
WGS_1984_TM_12_SE	5842	Angola - offshore north of 8°S	-8.01	10.41	-5.05	12.84
WGS_1984_TM_132_SE	2310	Indonesia - West Papua - Tangguh	-2.94	131.89	-1.97	133.82
WGS_1984_TM_36_SE	32766	Mozambique - offshore	-27.71	32.64	-10.09	43.03
WGS_1984_TM_60_SW	6703	Falkland Islands - offshore 63°W to 57°W	-56.25	-63.01	-47.68	-56.99
WGS_1984_TM_6_NE	2311	Nigeria - offshore	1.92	2.66	6.38	8.49
WGS_1984_TM_Zone_20N_(US_Feet)	8035	Trinidad and Tobago - offshore west of 60°W	9.83	-62.09	12.34	-59.99
WGS_1984_TM_Zone_21N_(US_Feet)	8036	Trinidad and Tobago - offshore east of 60°W	9.95	-60	12.19	-57.28
WGS_1984_TMzn35N	4037	Moldova - west of 30°E	45.44	26.63	48.47	30
WGS_1984_TMzn36N	4038	Moldova - east of 30°E	46.37	30	46.47	30.13
WGS_1984_Tobler_Cylindrical_I	54100	World	-90	-180	90	180
WGS_1984_Tobler_Cylindrical_II	54101	World	-90	-180	90	180
WGS_1984_Tripura	7786	India - Tripura	22.94	91.15	24.54	92.34
WGS_1984_USGS_Transantarctic_ Mountains	3294	Antarctica - Transantarctic mountains north of 80°S	-80	149.83	-68.6	174.01
WGS_1984_UTM_Gabon_TM	5223	Gabon - onshore	-3.98	8.65	2.32	14.52
WGS_1984_UTM_Gabon_TM_2011	5523	Gabon	-6.37	7.03	2.32	14.52
WGS_1984_UTM_Zone_10N	32610	World - N hemisphere - 126°W to 120°W - by country	0	-126	84	-120
WGS_1984_UTM_Zone_10S	32710	World - S hemisphere - 126°W to 120°W - by country	-80	-126	0	-120
WGS_1984_UTM_Zone_11N	32611	World - N hemisphere - 120°W to 114°W - by country	0	-120	84	-114
WGS_1984_UTM_Zone_11S	32711	World - S hemisphere - 120°W to 114°W - by country	-80	-120	0	-114
WGS_1984_UTM_Zone_12N	32612	World - N hemisphere - 114°W to 108°W - by country	0	-114	84	-108
WGS_1984_UTM_Zone_12S	32712	World - S hemisphere - 114°W to 108°W - by country	-80	-114	0	-108
WGS_1984_UTM_Zone_13N	32613	World - N hemisphere - 108°W to 102°W - by country	0	-108	84	-102
WGS_1984_UTM_Zone_13S	32713	World - S hemisphere - 108°W to 102°W - by country	-80	-108	0	-102
WGS_1984_UTM_Zone_14N	32614	World - N hemisphere - 102°W to 96°W - by country	0	-102	84	-96
WGS_1984_UTM_Zone_14S	32714	World - S hemisphere - 102°W to 96°W - by country	-80	-102	0	-96
WGS_1984_UTM_Zone_15N	32615	World - N hemisphere - 96°W to 90°W - by country	0	-96	84	-90
WGS_1984_UTM_Zone_15S	32715	World - S hemisphere - 96°W to 90°W - by country	-80	-96	0	-90
WGS_1984_UTM_Zone_16N	32616	World - N hemisphere - 90°W to 84°W - by country	0	-90	84	-84
WGS_1984_UTM_Zone_16S	32716	World - S hemisphere - 90°W to 84°W - by country	-80	-90	0	-84
WGS_1984_UTM_Zone_17N	32617	World - N hemisphere - 84°W to 78°W - by country	0	-84	84	-78
WGS_1984_UTM_Zone_17S	32717	World - S hemisphere - 84°W to 78°W - by country	-80	-84	0	-78
WGS_1984_UTM_Zone_18N	32618	World - N hemisphere - 78°W to 72°W - by country	0	-78	84	-72
WGS_1984_UTM_Zone_18S	32718	World - S hemisphere - 78°W to 72°W - by country	-80	-78	0	-72
WGS_1984_UTM_Zone_19N	32619	World - N hemisphere - 72°W to 66°W - by country	0	-72	84	-66
WGS_1984_UTM_Zone_19S	32719	World - S hemisphere - 72°W to 66°W - by country	-80	-72	0	-66
WGS_1984_UTM_Zone_1N	32601	World - N hemisphere - 180°W to 174°W - by country	0	-180	84	-174
WGS_1984_UTM_Zone_1S	32701	World - S hemisphere - 180°W to 174°W - by country	-80	-180	0	-174
WGS_1984_UTM_Zone_20N	32620	World - N hemisphere - 66°W to 60°W - by country	0	-66	84	-60
WGS_1984_UTM_Zone_20S	32720	World - S hemisphere - 66°W to 60°W - by country	-80	-66	0	-60
WGS_1984_UTM_Zone_21N	32621	World - N hemisphere - 60°W to 54°W - by country	0	-60	84	-54
WGS_1984_UTM_Zone_21S	32721	World - S hemisphere - 60°W to 54°W - by country	-80	-60	0	-54
WGS_1984_UTM_Zone_22N	32622	World - N hemisphere - 54°W to 48°W - by country	0	-54	84	-48
WGS_1984_UTM_Zone_22S	32722	World - S hemisphere - 54°W to 48°W - by country	-80	-54	0	-48
WGS_1984_UTM_Zone_23N	32623	World - N hemisphere - 48°W to 42°W - by country	0	-48	84	-42
WGS_1984_UTM_Zone_23S	32723	World - S hemisphere - 48°W to 42°W - by country	-80	-48	0	-42
WGS_1984_UTM_Zone_24N	32624	World - N hemisphere - 42°W to 36°W - by country	0	-42	84	-36
WGS_1984_UTM_Zone_24S	32724	World - S hemisphere - 42°W to 36°W - by country	-80	-42	0	-36
WGS_1984_UTM_Zone_25N	32625	World - N hemisphere - 36°W to 30°W - by country	0	-36	84	-30
WGS_1984_UTM_Zone_25S	32725	World - S hemisphere - 36°W to 30°W - by country	-80	-36	0	-30
WGS_1984_UTM_Zone_26N	32626	World - N hemisphere - 30°W to 24°W - by country	0	-30	84	-24
WGS_1984_UTM_Zone_26S	32726	World - S hemisphere - 30°W to 24°W - by country	-80	-30	0	-24
WGS_1984_UTM_Zone_27N	32627	World - N hemisphere - 24°W to 18°W - by country	0	-24	84	-18
WGS_1984_UTM_Zone_27S	32727	World - S hemisphere - 24°W to 18°W - by country	-80	-24	0	-18
WGS_1984_UTM_Zone_28N	32628	World - N hemisphere - 18°W to 12°W - by country	0	-18	84	-12
WGS_1984_UTM_Zone_28S	32728	World - S hemisphere - 18°W to 12°W - by country	-80	-18	0	-12
WGS_1984_UTM_Zone_29N	32629	World - N hemisphere - 12°W to 6°W - by country	0	-12	84	-6
WGS_1984_UTM_Zone_29S	32729	World - S hemisphere - 12°W to 6°W - by country	-80	-12	0	-6
WGS_1984_UTM_Zone_2N	32602	World - N hemisphere - 174°W to 168°W - by country	0	-174	84	-168
WGS_1984_UTM_Zone_2S	32702	World - S hemisphere - 174°W to 168°W - by country	-80	-174	0	-168
WGS_1984_UTM_Zone_30N	32630	World - N hemisphere - 6°W to 0°W - by country	0	-6	84	0
WGS_1984_UTM_Zone_30S	32730	World - S hemisphere - 6°W to 0°W - by country	-80	-6	0	0
WGS_1984_UTM_Zone_31N	32631	World - N hemisphere - 0°E to 6°E - by country	0	0	84	6
WGS_1984_UTM_Zone_31S	32731	World - S hemisphere - 0°E to 6°E - by country	-80	0	0	6
WGS_1984_UTM_Zone_32N	32632	World - N hemisphere - 6°E to 12°E - by country	0	6	84	12
WGS_1984_UTM_Zone_32S	32732	World - S hemisphere - 6°E to 12°E - by country	-80	6	0	12
WGS_1984_UTM_Zone_33N	32633	World - N hemisphere - 12°E to 18°E - by country	0	12	84	18
WGS_1984_UTM_Zone_33S	32733	World - S hemisphere - 12°E to 18°E - by country	-80	12	0	18
WGS_1984_UTM_Zone_34N	32634	World - N hemisphere - 18°E to 24°E - by country	0	18	84	24
WGS_1984_UTM_Zone_34S	32734	World - S hemisphere - 18°E to 24°E - by country	-80	18	0	24
WGS_1984_UTM_Zone_35N	32635	World - N hemisphere - 24°E to 30°E - by country	0	24	84	30
WGS_1984_UTM_Zone_35S	32735	World - S hemisphere - 24°E to 30°E - by country	-80	24	0	30
WGS_1984_UTM_Zone_36N	32636	World - N hemisphere - 30°E to 36°E - by country	0	30	84	36
WGS_1984_UTM_Zone_36S	32736	World - S hemisphere - 30°E to 36°E - by country	-80	30	0	36
WGS_1984_UTM_Zone_37N	32637	World - N hemisphere - 36°E to 42°E - by country	0	36	84	42
WGS_1984_UTM_Zone_37S	32737	World - S hemisphere - 36°E to 42°E - by country	-80	36	0	42
WGS_1984_UTM_Zone_38N	32638	World - N hemisphere - 42°E to 48°E - by country	0	42	84	48
WGS_1984_UTM_Zone_38S	32738	World - S hemisphere - 42°E to 48°E - by country	-80	42	0	48
WGS_1984_UTM_Zone_39N	32639	World - N hemisphere - 48°E to 54°E - by country	0	48	84	54
WGS_1984_UTM_Zone_39S	32739	World - S hemisphere - 48°E to 54°E - by country	-80	48	0	54
WGS_1984_UTM_Zone_3N	32603	World - N hemisphere - 168°W to 162°W - by country	0	-168	84	-162
WGS_1984_UTM_Zone_3S	32703	World - S hemisphere - 168°W to 162°W - by country	-80	-168	0	-162
WGS_1984_UTM_Zone_40N	32640	World - N hemisphere - 54°E to 60°E - by country	0	54	84	60
WGS_1984_UTM_Zone_40S	32740	World - S hemisphere - 54°E to 60°E - by country	-80	54	0	60
WGS_1984_UTM_Zone_41N	32641	World - N hemisphere - 60°E to 66°E - by country	0	60	84	66
WGS_1984_UTM_Zone_41S	32741	World - S hemisphere - 60°E to 66°E - by country	-80	60	0	66
WGS_1984_UTM_Zone_42N	32642	World - N hemisphere - 66°E to 72°E - by country	0	66	84	72
WGS_1984_UTM_Zone_42S	32742	World - S hemisphere - 66°E to 72°E - by country	-80	66	0	72
WGS_1984_UTM_Zone_43N	32643	World - N hemisphere - 72°E to 78°E - by country	0	72	84	78
WGS_1984_UTM_Zone_43S	32743	World - S hemisphere - 72°E to 78°E - by country	-80	72	0	78
WGS_1984_UTM_Zone_44N	32644	World - N hemisphere - 78°E to 84°E - by country	0	78	84	84
WGS_1984_UTM_Zone_44S	32744	World - S hemisphere - 78°E to 84°E - by country	-80	78	0	84
WGS_1984_UTM_Zone_45N	32645	World - N hemisphere - 84°E to 90°E - by country	0	84	84	90
WGS_1984_UTM_Zone_45S	32745	World - S hemisphere - 84°E to 90°E - by country	-80	84	0	90
WGS_1984_UTM_Zone_46N	32646	World - N hemisphere - 90°E to 96°E - by country	0	90	84	96
WGS_1984_UTM_Zone_46S	32746	World - S hemisphere - 90°E to 96°E - by country	-80	90	0	96
WGS_1984_UTM_Zone_47N	32647	World - N hemisphere - 96°E to 102°E - by country	0	96	84	102
WGS_1984_UTM_Zone_47S	32747	World - S hemisphere - 96°E to 102°E - by country	-80	96	0	102
WGS_1984_UTM_Zone_48N	32648	World - N hemisphere - 102°E to 108°E - by country	0	102	84	108
WGS_1984_UTM_Zone_48S	32748	World - S hemisphere - 102°E to 108°E - by country	-80	102	0	108
WGS_1984_UTM_Zone_49N	32649	World - N hemisphere - 108°E to 114°E - by country	0	108	84	114
WGS_1984_UTM_Zone_49S	32749	World - S hemisphere - 108°E to 114°E - by country	-80	108	0	114
WGS_1984_UTM_Zone_4N	32604	World - N hemisphere - 162°W to 156°W - by country	0	-162	84	-156
WGS_1984_UTM_Zone_4S	32704	World - S hemisphere - 162°W to 156°W - by country	-80	-162	0	-156
WGS_1984_UTM_Zone_50N	32650	World - N hemisphere - 114°E to 120°E - by country	0	114	84	120
WGS_1984_UTM_Zone_50S	32750	World - S hemisphere - 114°E to 120°E - by country	-80	114	0	120
WGS_1984_UTM_Zone_51N	32651	World - N hemisphere - 120°E to 126°E - by country	0	120	84	126
WGS_1984_UTM_Zone_51S	32751	World - S hemisphere - 120°E to 126°E - by country	-80	120	0	126
WGS_1984_UTM_Zone_52N	32652	World - N hemisphere - 126°E to 132°E - by country	0	126	84	132
WGS_1984_UTM_Zone_52S	32752	World - S hemisphere - 126°E to 132°E - by country	-80	126	0	132
WGS_1984_UTM_Zone_53N	32653	World - N hemisphere - 132°E to 138°E - by country	0	132	84	138
WGS_1984_UTM_Zone_53S	32753	World - S hemisphere - 132°E to 138°E - by country	-80	132	0	138
WGS_1984_UTM_Zone_54N	32654	World - N hemisphere - 138°E to 144°E - by country	0	138	84	144
WGS_1984_UTM_Zone_54S	32754	World - S hemisphere - 138°E to 144°E - by country	-80	138	0	144
WGS_1984_UTM_Zone_55N	32655	World - N hemisphere - 144°E to 150°E - by country	0	144	84	150
WGS_1984_UTM_Zone_55S	32755	World - S hemisphere - 144°E to 150°E - by country	-80	144	0	150
WGS_1984_UTM_Zone_56N	32656	World - N hemisphere - 150°E to 156°E - by country	0	150	84	156
WGS_1984_UTM_Zone_56S	32756	World - S hemisphere - 150°E to 156°E - by country	-80	150	0	156
WGS_1984_UTM_Zone_57N	32657	World - N hemisphere - 156°E to 162°E - by country	0	156	84	162
WGS_1984_UTM_Zone_57S	32757	World - S hemisphere - 156°E to 162°E - by country	-80	156	0	162
WGS_1984_UTM_Zone_58N	32658	World - N hemisphere - 162°E to 168°E - by country	0	162	84	168
WGS_1984_UTM_Zone_58S	32758	World - S hemisphere - 162°E to 168°E - by country	-80	162	0	168
WGS_1984_UTM_Zone_59N	32659	World - N hemisphere - 168°E to 174°E - by country	0	168	84	174
WGS_1984_UTM_Zone_59S	32759	World - S hemisphere - 168°E to 174°E - by country	-80	168	0	174
WGS_1984_UTM_Zone_5N	32605	World - N hemisphere - 156°W to 150°W - by country	0	-156	84	-150
WGS_1984_UTM_Zone_5S	32705	World - S hemisphere - 156°W to 150°W - by country	-80	-156	0	-150
WGS_1984_UTM_Zone_60N	32660	World - N hemisphere - 174°E to 180°E - by country	0	174	84	180
WGS_1984_UTM_Zone_60S	32760	World - S hemisphere - 174°E to 180°E - by country	-80	174	0	180
WGS_1984_UTM_Zone_6N	32606	World - N hemisphere - 150°W to 144°W - by country	0	-150	84	-144
WGS_1984_UTM_Zone_6S	32706	World - S hemisphere - 150°W to 144°W - by country	-80	-150	0	-144
WGS_1984_UTM_Zone_7N	32607	World - N hemisphere - 144°W to 138°W - by country	0	-144	84	-138
WGS_1984_UTM_Zone_7S	32707	World - S hemisphere - 144°W to 138°W - by country	-80	-144	0	-138
WGS_1984_UTM_Zone_8N	32608	World - N hemisphere - 138°W to 132°W - by country	0	-138	84	-132
WGS_1984_UTM_Zone_8S	32708	World - S hemisphere - 138°W to 132°W - by country	-80	-138	0	-132
WGS_1984_UTM_Zone_9N	32609	World - N hemisphere - 132°W to 126°W - by country	0	-132	84	-126
WGS_1984_UTM_Zone_9S	32709	World - S hemisphere - 132°W to 126°W - by country	-80	-132	0	-126
WGS_1984_Uttaranchal	7776	India - Uttarakhand	28.71	77.56	31.48	81.02
WGS_1984_Uttar_Pradesh	7775	India - Uttar Pradesh	23.87	77.08	30.42	84.64
WGS_1984_World_Equidistant_ Cylindrical	4087	World	-90	-180	90	180
WGS_1984_Web_Mercator_Auxiliary_ Sphere	3857	World - 85°S to 85°N	-85.06	-180	85.06	180
WGS_1984_West_Bengal	7787	India - West Bengal	21.49	85.82	27.23	89.88
WGS_1984_World_Mercator	3395	World - between 80°S and 84°N	-80	-180	84	180
World_Aitoff	54043	World	-90	-180	90	180
World_Azimuthal_Equidistant	54032	World	-90	-180	90	180
World_Behrmann	54017	World	-90	-180	90	180
World_Bonne	54024	World	-90	-180	90	180
World_Cassini	54028	World	-90	-180	90	180
World_Compact_Miller	54080	World	-90	-180	90	180
World_Craster_Parabolic	54046	World	-90	-180	90	180
World_Cube	54051	World	-90	-180	90	180
World_Cylindrical_Equal_Area	54034	World	-90	-180	90	180
World_Eckert_I	54015	World	-90	-180	90	180
World_Eckert_II	54014	World	-90	-180	90	180
World_Eckert_III	54013	World	-90	-180	90	180
World_Eckert_IV	54012	World	-90	-180	90	180
World_Eckert_V	54011	World	-90	-180	90	180
World_Eckert_VI	54010	World	-90	-180	90	180
WGS_1984_Equal_Earth_Greenwich	8857	World	-90	-180	90	180
WGS_1984_Equal_Earth_Americas	8858	World	-90	-180	90	180
WGS_1984_Equal_Earth_Asia_Pacific	8859	World	-90	-180	90	180
World_Equidistant_Conic	54027	World	-90	-180	90	180
World_Equidistant_Cylindrical	54002	World	-90	-180	90	180
World_Equidistant_Cylindrical_(Sphere)	4088	World	-90	-180	90	180
World_Flat_Polar_Quartic	54045	World	-90	-180	90	180
World_Fuller	54050	World	-90	-180	90	180
World_Gall_Stereographic	54016	World	-90	-180	90	180
World_Goode_Homolosine_Land	54052	World	-90	-180	90	180
World_Goode_Homolosine_Ocean	54053	World	-90	-180	90	180
World_Hammer_Aitoff	54044	World	-90	-180	90	180
World_Hotine	54025	World	-90	-180	90	180
World_Loximuthal	54023	World	-90	-180	90	180
World_Mercator	54004	World	-90	-180	90	180
World_Miller_Cylindrical	54003	World	-90	-180	90	180
World_Mollweide	54009	World	-90	-180	90	180
World_Natural_Earth	54077	World	-90	-180	90	180
World_Natural_Earth_II	54078	World	-90	-180	90	180
World_Patterson	54079	World	-90	-180	90	180
World_Plate_Carree	54001	World	-90	-180	90	180
World_Polyconic	54021	World	-90	-180	90	180
World_Quartic_Authalic	54022	World	-90	-180	90	180
World_Robinson	54030	World	-90	-180	90	180
World_Sinusoidal	54008	World	-90	-180	90	180
World_Stereographic	54026	World	-90	-180	90	180
World_Times	54048	World	-90	-180	90	180
World_Two_Point_Equidistant	54031	World	-90	-180	90	180
World_Van_der_Grinten_I	54029	World	-90	-180	90	180
World_Vertical_Perspective	54049	World	-90	-180	90	180
World_Wagner_IV	54074	World	-90	-180	90	180
World_Wagner_V	54075	World	-90	-180	90	180
World_Wagner_VII	54076	World	-90	-180	90	180
World_Winkel_I	54018	World	-90	-180	90	180
World_Winkel_II	54019	World	-90	-180	90	180
World_Winkel_Tripel_NGS	54042	World	-90	-180	90	180
Xian_1980_3_Degree_GK_CM_102E	2379	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
Xian_1980_3_Degree_GK_CM_105E	2380	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
Xian_1980_3_Degree_GK_CM_108E	2381	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
Xian_1980_3_Degree_GK_CM_111E	2382	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
Xian_1980_3_Degree_GK_CM_114E	2383	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
Xian_1980_3_Degree_GK_CM_117E	2384	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
Xian_1980_3_Degree_GK_CM_120E	2385	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
Xian_1980_3_Degree_GK_CM_123E	2386	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
Xian_1980_3_Degree_GK_CM_126E	2387	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
Xian_1980_3_Degree_GK_CM_129E	2388	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
Xian_1980_3_Degree_GK_CM_132E	2389	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
Xian_1980_3_Degree_GK_CM_135E	2390	China - east of 133.5°E	45.85	133.5	48.4	134.77
Xian_1980_3_Degree_GK_CM_75E	2370	China - west of 76.5°E	35.81	73.62	40.65	76.5
Xian_1980_3_Degree_GK_CM_78E	2371	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
Xian_1980_3_Degree_GK_CM_81E	2372	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
Xian_1980_3_Degree_GK_CM_84E	2373	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
Xian_1980_3_Degree_GK_CM_87E	2374	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
Xian_1980_3_Degree_GK_CM_90E	2375	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
Xian_1980_3_Degree_GK_CM_93E	2376	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
Xian_1980_3_Degree_GK_CM_96E	2377	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
Xian_1980_3_Degree_GK_CM_99E	2378	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
Xian_1980_3_Degree_GK_Zone_25	2349	China - west of 76.5°E	35.81	73.62	40.65	76.5
Xian_1980_3_Degree_GK_Zone_26	2350	China - 76.5°E to 79.5°E	31.03	76.5	41.83	79.5
Xian_1980_3_Degree_GK_Zone_27	2351	China - 79.5°E to 82.5°E	29.95	79.5	45.88	82.51
Xian_1980_3_Degree_GK_Zone_28	2352	China - 82.5°E to 85.5°E	28.26	82.5	47.23	85.5
Xian_1980_3_Degree_GK_Zone_29	2353	China - 85.5°E to 88.5°E	27.8	85.5	49.18	88.5
Xian_1980_3_Degree_GK_Zone_30	2354	China - 88.5°E to 91.5°E	27.32	88.49	48.42	91.51
Xian_1980_3_Degree_GK_Zone_31	2355	China - 91.5°E to 94.5°E	27.71	91.5	45.13	94.5
Xian_1980_3_Degree_GK_Zone_32	2356	China - 94.5°E to 97.5°E	28.23	94.5	44.5	97.51
Xian_1980_3_Degree_GK_Zone_33	2357	China - 97.5°E to 100.5°E	21.43	97.5	42.76	100.5
Xian_1980_3_Degree_GK_Zone_34	2358	China - 100.5°E to 103.5°E	21.13	100.5	42.69	103.5
Xian_1980_3_Degree_GK_Zone_35	2359	China - 103.5°E to 106.5°E	22.5	103.5	42.21	106.51
Xian_1980_3_Degree_GK_Zone_36	2360	China - 106.5°E to 109.5°E onshore	18.19	106.5	42.47	109.51
Xian_1980_3_Degree_GK_Zone_37	2361	China - 109.5°E to 112.5°E onshore	18.11	109.5	45.11	112.5
Xian_1980_3_Degree_GK_Zone_38	2362	China - 112.5°E to 115.5°E onshore	21.52	112.5	45.45	115.5
Xian_1980_3_Degree_GK_Zone_39	2363	China - 115.5°E to 118.5°E onshore	22.6	115.5	49.88	118.5
Xian_1980_3_Degree_GK_Zone_40	2364	China - 118.5°E to 121.5°E onshore	24.43	118.5	53.33	121.5
Xian_1980_3_Degree_GK_Zone_41	2365	China - 121.5°E to 124.5°E onshore	28.22	121.5	53.56	124.5
Xian_1980_3_Degree_GK_Zone_42	2366	China - 124.5°E to 127.5°E onshore	40.19	124.5	53.2	127.5
Xian_1980_3_Degree_GK_Zone_43	2367	China - 127.5°E to 130.5°E	41.37	127.5	50.25	130.5
Xian_1980_3_Degree_GK_Zone_44	2368	China - 130.5°E to 133.5°E	42.42	130.5	48.88	133.5
Xian_1980_3_Degree_GK_Zone_45	2369	China - east of 133.5°E	45.85	133.5	48.4	134.77
Xian_1980_GK_CM_105E	2343	China - 102°E to 108°E onshore	21.53	102	42.47	108
Xian_1980_GK_CM_111E	2344	China - 108°E to 114°E onshore	18.11	108	45.11	114
Xian_1980_GK_CM_117E	2345	China - 114°E to 120°E onshore	22.14	114	51.52	120
Xian_1980_GK_CM_123E	2346	China - 120°E to 126°E onshore	26.34	120	53.56	126
Xian_1980_GK_CM_129E	2347	China - 126°E to 132°E onshore	40.89	126	52.79	132
Xian_1980_GK_CM_135E	2348	China - east of 132°E	45.02	132	48.4	134.77
Xian_1980_GK_CM_75E	2338	China - west of 78°E	35.42	73.62	41.07	78.01
Xian_1980_GK_CM_81E	2339	China - 78°E to 84°E	29.16	77.98	47.23	84
Xian_1980_GK_CM_87E	2340	China - 84°E to 90°E	27.32	84	49.18	90
Xian_1980_GK_CM_93E	2341	China - 90°E to 96°E	27.71	90	47.9	96.01
Xian_1980_GK_CM_99E	2342	China - 96°E to 102°E	21.13	96	43.18	102.01
Xian_1980_GK_Zone_13	2327	China - west of 78°E	35.42	73.62	41.07	78.01
Xian_1980_GK_Zone_14	2328	China - 78°E to 84°E	29.16	77.98	47.23	84
Xian_1980_GK_Zone_15	2329	China - 84°E to 90°E	27.32	84	49.18	90
Xian_1980_GK_Zone_16	2330	China - 90°E to 96°E	27.71	90	47.9	96.01
Xian_1980_GK_Zone_17	2331	China - 96°E to 102°E	21.13	96	43.18	102.01
Xian_1980_GK_Zone_18	2332	China - 102°E to 108°E onshore	21.53	102	42.47	108
Xian_1980_GK_Zone_19	2333	China - 108°E to 114°E onshore	18.11	108	45.11	114
Xian_1980_GK_Zone_20	2334	China - 114°E to 120°E onshore	22.14	114	51.52	120
Xian_1980_GK_Zone_21	2335	China - 120°E to 126°E onshore	26.34	120	53.56	126
Xian_1980_GK_Zone_22	2336	China - 126°E to 132°E onshore	40.89	126	52.79	132
Xian_1980_GK_Zone_23	2337	China - east of 132°E	45.02	132	48.4	134.77
Yemen_NGN_1996_UTM_Zone_37N	5836	Yemen - west of 42°E	14.73	41.08	16.36	42
Yemen_NGN_1996_UTM_Zone_38N	2089	Yemen - 42°E to 48°E	11.57	42	17.95	48.01
Yemen_NGN_1996_UTM_Zone_39N	2090	Yemen - 48°E to 54°E	9.45	48	19	54.01
Yemen_NGN_1996_UTM_Zone_40N	5837	Yemen - east of 54°E	8.95	54	14.95	57.96
Yoff_1972_UTM_Zone_28N	31028	Senegal	10.64	-20.22	16.7	-11.36
Zanderij_1972_UTM_Zone_21N	31121	Suriname	1.83	-58.08	9.35	-52.66
Zanderij_Suriname_Old_TM	31170	Suriname - onshore	1.83	-58.08	6.06	-53.95
Zanderij_Suriname_TM	31171	Suriname - onshore	1.83	-58.08	6.06	-53.95
Zanderij_TM_54_NW	31154	Suriname - offshore	5.34	-57.25	9.35	-52.66