Section Two - Geodesy

While GIS Geographic Information Systems the software used to create, store, and manage spatial data, analyze spatial problems, and display the data in cartographic layouts   Geographic Information Sciences is the science of solving problems using both spatial and non-spatial data Attributes related to a location but not describing its physical placement in space, such as information about a tree's age, type, and health. , it is far from the first science to be concerned with such measurements. The first Earth Science dedicated to the topic was geodesy the science of measuring and monitoring the size and shape of the Earth and the location of points on its surface , defined as: the science of measuring and monitoring the size and shape of the Earth and the location of points on its surface^[1].  The very first step in creating our Earth Address System (which is made-up thing used to explain the process of creating a Geographic Coordinate System, the real term for labeling locations on the Earths' surface) is to know just how big the Earth is and how we need to go about creating our grid and placing our labels. 

2.2.1: A Brief History of Measuring the Earth

We as humans, in addition to our love of labeling things, love to measure things. We need to know how big, how far, how dense, how quickly ... all the things that later became Geospatial Sciences (the larger branch of science under which GIS Geographic Information Systems the software used to create, store, and manage spatial data, analyze spatial problems, and display the data in cartographic layouts   Geographic Information Sciences falls). Somewhere after the decision that the Earth was indeed round and not flat (really, it is), great men of science began to figure out a way to measure an object upon which the stood and had no means of taking a step back to get a relative view. There were several folks who did so, but we are only going to take a minute to look at two - Eratosthenes of Cyrene and Abu Rayhan al-Biruni.

Eratosthenes

A long time ago (somewhere around 200 BCE), in a galaxy far, far, away (Egypt), there lived a Greek scholar called Eratosthenes of Cyrene.

FIGURE 2.1: Eratosthenes (276 -194 BCE)

Using this knowledge, combined with the facts: 

1. The sun was directly over the Tropic of Cancer at midday on the Summer Solstice
2. Cyrene was located on the Tropic of Cancer (not exactly, but Eratosthenes thought so at the time)
3. Alexandria was 500 miles due north of Cyrene (or so Eratosthenes thought)

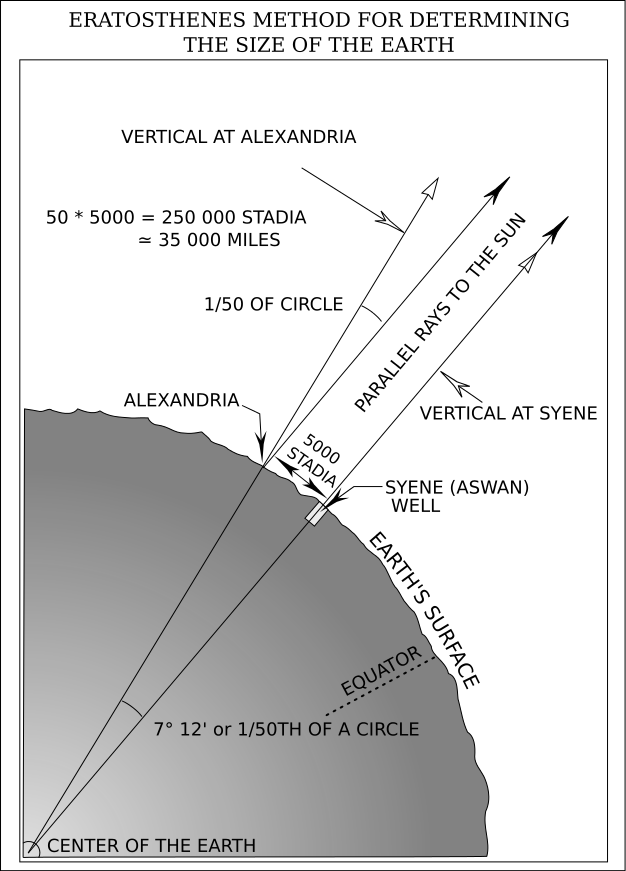
Eratosthenes discovered that on the Summer Solstice (the longest day of the year) a well in the town of Cyrene was illuminated to the bottom at midday. He also observed that on the same day at a flag pole in Alexandria, the sun did not completely illuminate, but instead cast a small shadow (with a measured angle of 7° 12’ or 1/50the of a circle).

Eratosthenes calculated the circumference of the Earth must be 50 times the distance from Cyrene to Alexandria, or 25,010 miles (since the sun cast no shadow in Cyrene and a shadow equal to 1/50the of a circle 500 miles north).

Considering Eratosthenes was using ‘facts’ which were not exactly correct (Alexandria sat offset to Cyrene by 3° 3’, or 210.5 miles, not due north; Cyrene was 37 miles from the Tropic of Cancer, not directly on it; and the distance from Cyrene to Alexandria was 453 mile, not 500 miles), his estimation of the Earth’s circumference was less the 4% off of the actual calculation of 24,901.55 miles. I guess all his facts were incorrect in just the right proportions!

FIGURE 2.2: Eratosthenes’s Method for Determining the Size of the Earth

Al-Biruni

Even though Eratosthenes was pretty darn close, geodesy the science of measuring and monitoring the size and shape of the Earth and the location of points on its surface didn’t stop there. Abu Rayhan al-Biruni (4/5 September 973 – 13 December 1048) lived in the Persian Empire and his hobbies were mathematics, astronomy, physics, and natural sciences, but did not like long walks through hot deserts. He was determined to develop a method of measuring the Earth using mathematics that didn’t require hot walks in dusty deserts.

FIGURE 2.3: Abu Rayhan al-Biruni (4/5 September 973 – 13 December 1048)

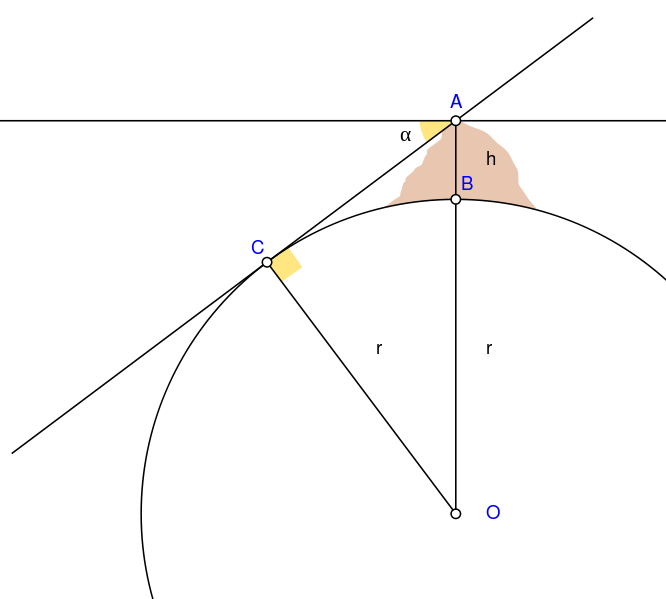
Using an astrolabe to measure an angle between a grassy plain where he stood and the top of a mountain (of which he knew the elevation the vertical distance between local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features and a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface ), in combination with measuring the dip angle (a phenomenon with the Earth’s magnetic fields that results in the compass needle to point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. to ‘magnetic north’ instead of ‘geographic north’; where the need to set a compasses declination comes from) from the top of that mountain, al-Biruni was able to apply trigonometry and the law of sines to calculate the radius of the Earth. With better luck then Eratosthenes, al-Biruni’s calculation of the 3,939.43 miles was just 10.43 miles less then the modern accepted measurement of 3,949.86 miles. All at the ripe old age of 17.

By the age of 22, he had written papers on the study of projections (making the round Earth into a flat map) and was the first to describe azimuthal equidistant projection technically: the result of using one of variety of methods to transfer the geographic locations of features from a geographic coordinate system to a developable surface everyday use: any coordinate system, geographic or projected , a method which preserved distances (at the expense of shape). al-Biruni’s talent and notoriety with cartography, measuring accurate distances between cities, and later developing methods for recording precise latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude locations, mountain heights, and valley depths, kept him busy for many years, earning him the title “Father of Geodesy”.

YouTube Break

Classical geodesy, defined as the area of science concerned with length of day, measuring the size of the Earth, measuring and mapping the ocean floor, the geometry of Earth, creating reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid and transformations, and creating accurate location methods using non-digital methods, is the predecessor to modern geodesy precise global and regional locations, both horizontal and vertical (along the Earth and above the Earth), mapping the land sea, and ice, and determining the variations in the Earth’s gravitational pull and how this effects measurements . Modern geodesy is focused on many of the same areas, but utilize digital measurement methods such as GPS, satellites, and GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts   Geographic Information Sciences software.

Modern geodesy focuses on more precise global and regional locations, both horizontal and vertical (along the Earth and above the Earth), mapping the land sea, and ice, and determining the variations in the Earth’s gravitational pull and how this effects measurements. Global and local measurements are focused on surface deformation, crustal motion, polar motion, earth rotation, tides, water cycle, mass transport, etc, while sea measurements look at the changing sea level, the state of the ocean, circulations patterns, and sea ice levels and locations. These measurements assist in studies surrounding climate change, geohazards such as earthquakes and tsunamis and their effects, and environmental changes.

FIGURE 2.5: Examples of Modern Geodesy
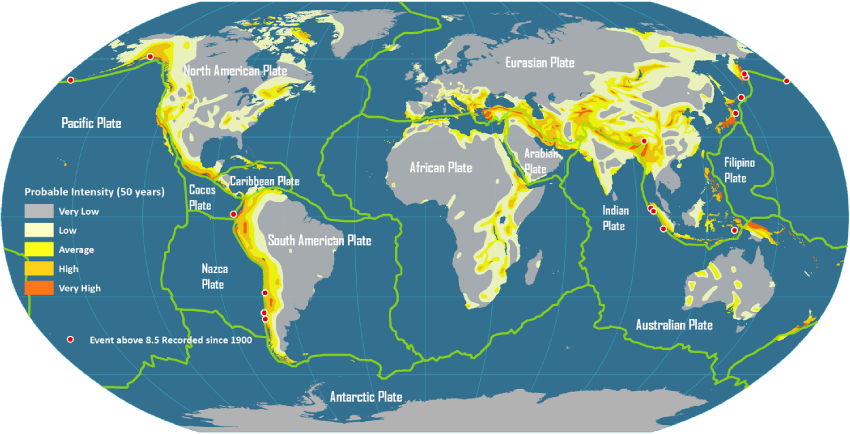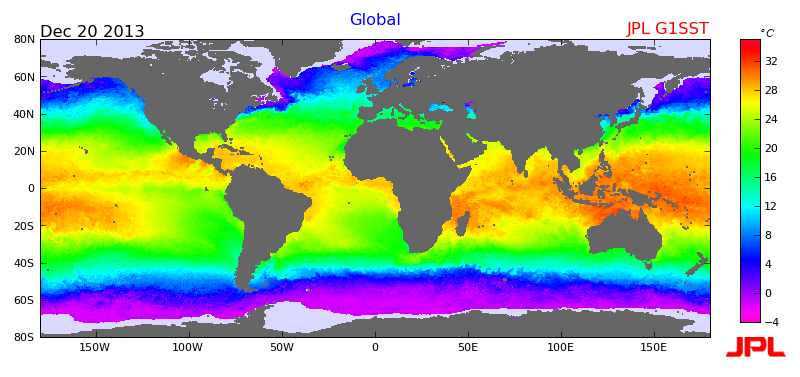Map of Global Tectonic Plates and Locations of Geohazards	Map of Average Sea Surface Temperature

Concept Quiz