For as long as humans have had the goal to explore our planet, they have also had the need to devise a navigation method to make this process easier, and more importantly, a method which was reliable and repeatable. As these exploration and discovery missions took explorers over longer distances and away from land, which is super handy for sighting back to and knowing where you are, a world-wide system that could be used day or night was needed. With a rather long history of discovery, trail, and error, latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude became a world-wide grid system, giving an explorer the ability to know where they were at all times, with a general error of about 10 feet. Not too bad without a GPS Global Positioning System: A satellite-based navigation system owned and operated by the United States Department of Defense that provides location and time information anywhere on Earth. receiver!
Geographic grids are created when a grid is applied to the Earth (initially a sphere for easy measuring, as we will see in this section, then later, that 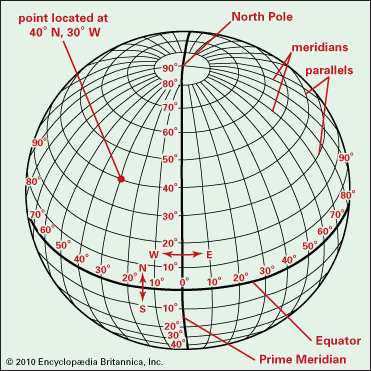 sphere is transformed into an ellipsoid) and the intersections are labeled via a Cartesian Coordinate system method. In this section, we will look at the specifics of creating that grid, by first by creating a sphere-based Earth-centered, Earth-fixed coordinate system (EFEC coordinate system) Earth-centered, Earth-fixed coordinate systems use the center of the Earth as a start
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
for measurements, while local-north systems use a smaller area affixed to the Earth’s surface as the start
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
). ECEF coordinate system require us to select a principle meridian (the north-south line from which to establish the X origin
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
, aka the place to start counting) and an before laying out the grid. Since the goal of an ECEF coordinate systems is to label locations on a 3D sphere, we can't efficiently use a linear unit of measure, like feet or meters. As we will see when the lines are drawn and the labels placed, using angles to establish measurements will be a boatload easier than using linear units, which would only be accomplished by wrapping an imaginary cloth tape measure around the Earth, which wouldn't lay flat, and really only measure the circumference, and what would the circumference even tell us .... you get it ... or you will when we look at establishing the line of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
and longitude.
sphere is transformed into an ellipsoid) and the intersections are labeled via a Cartesian Coordinate system method. In this section, we will look at the specifics of creating that grid, by first by creating a sphere-based Earth-centered, Earth-fixed coordinate system (EFEC coordinate system) Earth-centered, Earth-fixed coordinate systems use the center of the Earth as a start
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
for measurements, while local-north systems use a smaller area affixed to the Earth’s surface as the start
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
). ECEF coordinate system require us to select a principle meridian (the north-south line from which to establish the X origin
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
, aka the place to start counting) and an before laying out the grid. Since the goal of an ECEF coordinate systems is to label locations on a 3D sphere, we can't efficiently use a linear unit of measure, like feet or meters. As we will see when the lines are drawn and the labels placed, using angles to establish measurements will be a boatload easier than using linear units, which would only be accomplished by wrapping an imaginary cloth tape measure around the Earth, which wouldn't lay flat, and really only measure the circumference, and what would the circumference even tell us .... you get it ... or you will when we look at establishing the line of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
and longitude.
longitude is an and is just one example of a geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. , utilizing a specific principle meridian, the Prime Median, and degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° as the angular unit of measure the selected units for measuring angles. Choices include degree and radians. to label and later be able to navigate to locations on the Earth’s surface.
Geographic grids, it should be noted, are not a complete geographic coordinate system nor are they a datum. Latitude and longitude, albeit the most common - is not the only geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. out there. All of this reading is working towards the established goal of creating a tied down, worldwide "address system" we call a geographic coordinate system. The GCS is made up of two parts, one of which is a datum (which we will look at in the next section) and the other of which is geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. (which we are about to see requires an ECEF Coordinate System to be transformation into a reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid ).
Concept Quiz
2.4.1: Cartesian Coordinate Systems
A Cartesian coordinate system An equally spaced grid that exists in a single geometric plane where intersections of perpendicular lines are labeled with the count of units from a specified origin (0,0) point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , created by René Descartes in 1637, is defined as an equally spaced grid that exists in a single geometric plane where intersections of perpendicular lines are labeled with the count of units from a specified (0,0) point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. . You most likely learned all about Cartesian Coordinate Systems in grade school or jr. high. Each grid has a 0,0 point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. at the origin of the system, and each intersection of the X and Y lines are labeled according to how far said intersection is from the origin.
| FIGURE 2.16: Cartesian Coordinate System |
|---|
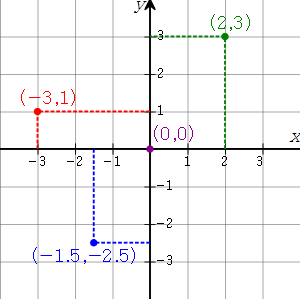 |
| In the example, the red point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. is defined (labeled) as (-3,1) after counting left (negative) three spaces and up (positive) one space from the purple (0,0) point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. . The green point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. is defined as (2,3) by counting two spaces on the X axis and 3 spaces on the Y axis. Finally, the blue point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. is defined as (-1.5, -2.5) utilizing the same method. |
In cartography and GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences , each datum has an origin and labeled points where the X and Y (and since datums are 3D, the Z) lines intersect. In the next section we will look at one method of labeling those intersections using latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude, but for now we will just look at how the 2D XY values reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid is connected to the 3D Z value geoid a model of the variation between global mean (average) sea level and local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features , which is used to measure precise elevations on the topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." .
Concept Quiz
2.4.2: Latitude
 Lines of Latitude (
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
(n.) late 14c., "breadth," from Old French
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
(13c.) and directly from Latin latitudo "breadth, width, extent, size," from latus "wide,") or parallels are the east-west portion of the grid, running horizontally - along the horizon. Using the Equator as a starting
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
for the
geographic grid
the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a
principal meridian
the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian.
, historically,
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
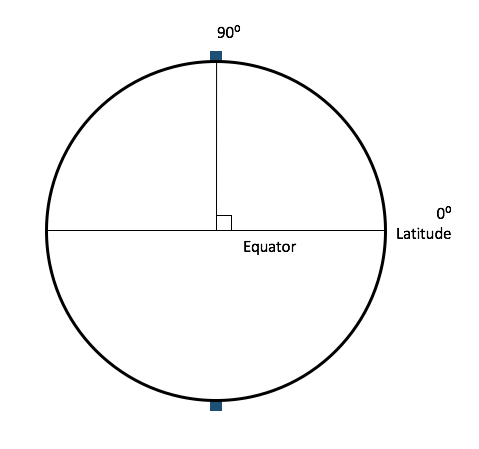
was easier to compute and comprehend than longitude (north-south lines), as splitting the Earth in half in the middle was simple to understand and easy to start with. Starting at the Equator, lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
use an angle system based upon a right triangle, encircling the earth at each of the 90
degrees
measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by °
North and South. The best way to understand how lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
are labeled is to look at the process it takes to create the lines from scratch.
Lines of Latitude (
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
(n.) late 14c., "breadth," from Old French
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
(13c.) and directly from Latin latitudo "breadth, width, extent, size," from latus "wide,") or parallels are the east-west portion of the grid, running horizontally - along the horizon. Using the Equator as a starting
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
for the
geographic grid
the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a
principal meridian
the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian.
, historically,
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
was easier to compute and comprehend than longitude (north-south lines), as splitting the Earth in half in the middle was simple to understand and easy to start with. Starting at the Equator, lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
use an angle system based upon a right triangle, encircling the earth at each of the 90
degrees
measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by °
North and South. The best way to understand how lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
are labeled is to look at the process it takes to create the lines from scratch.
| Sidebar: Let’s state a few more facts before we move on. | |
|---|---|
Great. We have drawn:
| 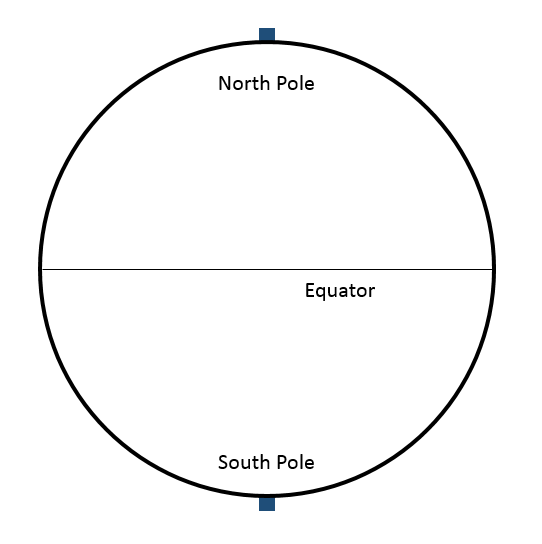 |
| Step 3. Mark all the angles between 0° and 89° and connect them from east to west | |
|---|---|
If we add in each angle from 1° to 89°, then from that point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , draw a straight line to the other side of our circle, we see we’ve created a series of 90 parallel lines running from the North Pole to the Equator, or the lines of Northern Latitude. If we mark a point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. representing Denver, we would need to start at the Equator and count up 39 lines of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° , then drop the point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. . To create the lines of Southern Latitude, we simple repeat this process starting at the South Pole and moving up.
| 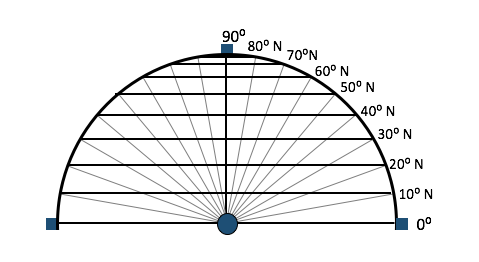 |
| Step 4. Find the distance between lines of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° |
|---|
When the circumference of the Earth is divided by 360 (total degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° in a circle), each line of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° is 111 kilometers or 68.972 miles (we will just round that up to 69 miles) from the next. Which by navigation standards is like getting lost on the way to Denver and ending up in Fort Collins.
|
| Step 5. Invent minutes "arc minute" 1/60th of a degree. Usually denoted by " and seconds arc minute. 1/60th of an arc minute; 1/3600 of a degree. Usually denoted by ' to better divide up the Earth’s circumference |
|---|
| To reduce the error created using a system with an accuracy of 69 miles, each degree was divided into 60 equal parts, or arc
minutes
"arc minute" 1/60th of a degree. Usually denoted by "
. Just as there are sixty
minutes
"arc minute" 1/60th of a degree. Usually denoted by "
on the clock, and it takes all sixty
minutes
"arc minute" 1/60th of a degree. Usually denoted by "
for the hour hand to travel from the 12 back to the 12, there are 60 arc
minutes
"arc minute" 1/60th of a degree. Usually denoted by "
in a degree. By dividing each degree into sixty equal parts and doing a bit of math, we can determine each arc minute is equal to 1.15 statute miles (or 1 nautical mile, since nautical and statute miles were based upon two different measurement systems)4. Breaking down each degree into arc minutes "arc minute" 1/60th of a degree. Usually denoted by " (which in GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences is simply shortened to ‘ minutes "arc minute" 1/60th of a degree. Usually denoted by " ’), navigation accuracy was dramatically improved. Yet, one nautical mile was still a bit course to navigate by, so the arc minute was broken into sixty equal parts to create the arc second. Arc seconds arc minute. 1/60th of an arc minute; 1/3600 of a degree. Usually denoted by ' (or just ‘ seconds arc minute. 1/60th of an arc minute; 1/3600 of a degree. Usually denoted by ' ’ in GIS Geographic Information Systems the software used to create, store, and manage spatial data Data that deals with location, such as lists of addresses, the footprint of a building, the boundaries of cities and counties, etc. , analyze spatial problems, and display the data in cartographic layouts Geographic Information Sciences ) measure in at roughly two-tenths of a mile, or about 121 feet (nautical) or 105 feet (statute). In modern terms, where even a smart phone is capable of being accurate down to about a foot, 100 feet seems like a pretty big margin of error, but when you think of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude in navigational terms, if Siri is telling you your destination is on the right but that Taco Bell is still 100 feet away, its pretty darn good |
Concept Quiz
2.4.3: Longitude
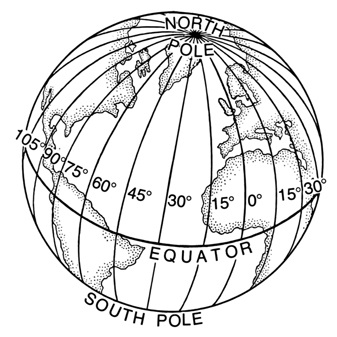 Lines of longitude (late Middle English (also denoting length and tallness): from Latin longitudo, from longus ‘long.’) or meridians are similar to
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
in the fact they divide the Earth into equal parts, but a different due to the fact that all lines of longitude all pass through the North and South poles, creating what looks like a spider web when viewed from the top down. The convergence of lines at the North and South poles results in the distance between lines of longitude not being an equal measure of 69 miles for the entire distance like lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
, but a variation between 0 miles at the poles and 69 miles at the Equator.
Lines of longitude (late Middle English (also denoting length and tallness): from Latin longitudo, from longus ‘long.’) or meridians are similar to
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
in the fact they divide the Earth into equal parts, but a different due to the fact that all lines of longitude all pass through the North and South poles, creating what looks like a spider web when viewed from the top down. The convergence of lines at the North and South poles results in the distance between lines of longitude not being an equal measure of 69 miles for the entire distance like lines of
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
, but a variation between 0 miles at the poles and 69 miles at the Equator.
To solve for the variation, multiply either 68.972 miles or 111 kilometers by the cosine of the latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° for which the longitude measurement is being taken. For example, Denver, CO is at 39° 44" 31.3548' N, 104° 59 29.5116" W. To find the distance between the lines of longitude (in this case, 104° and 103° or 105° along the 39the parallel), first find the cosine of the latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° (cosine of 39° = 0.777), then multiply it by 68.972 miles (68.972 * 0.777) which would equal 54.38 miles. In other words, if you walked north along 104° W from the 38the to the 39the parallel, you would walk 68.972 miles, and if you continued the journey on the the 40the parallel, you would walk another 68.972 miles. However, if you were to walk west along the 39the parallel from 104°W to 105°W, you would walk 54.38 miles. If you moved that journey north one degree of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and walk west along the 38the parallel from 104°W to 105°W, you would only walk 54.33 miles (68.972 * 0.788), a difference of only 0.03 miles, but indeed a shorter distance.
With lines of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° , there is a logical start point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. : divide the sphere in half creating the equator. But when it comes to lines of longitude, the part where the divisions are made by drawing a line from the North to the South pole is logical, deciding where to put the zero line, or the prime meridian, is a bit less obvious. So a place was chosen - Greenwich, England5.
While lines of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° are measured as angles between the North (or South) pole and the equator, angles which measure lines of longitude start at the Prime Meridian the name of the principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. in the latitude/longitude system and travel along the Equator marking each degree to the west until the reaching the other half of the Prime Meridian the name of the principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. in the latitude/longitude system , this creates 180 marks (and moving from the Prime Meridian the name of the principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. in the latitude/longitude system east makes a maximum of 180 marks east, for a total of 360 degrees measurement of plane angle, representing 1⁄360 of a full rotation (circle). In full, a degree of arc or arc degree. Usually denoted by ° , a full circle)
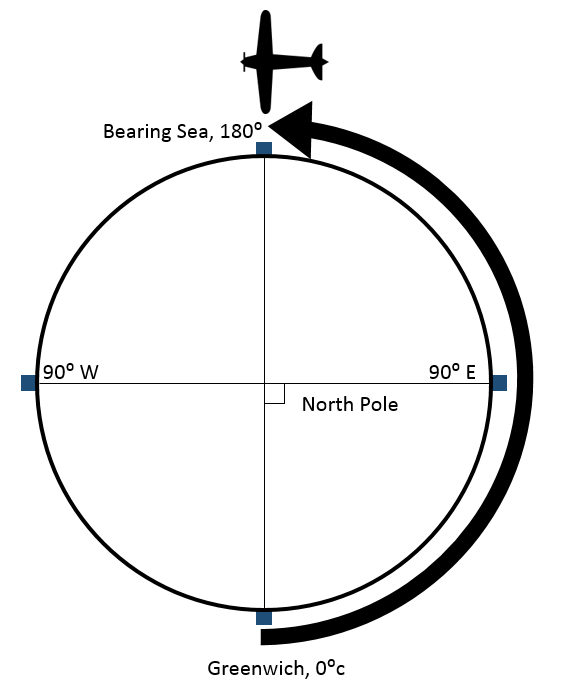
| Creating Lines of Longitude from Scratch, Step 1. Draw the Earth as Circle. | |
|---|---|
| First, we are going to draw a new circle to represent the Earth. Since we are looking down at the North Pole from space, we are going to place a single dot right in the middle of the circle to represent the North Pole. Since we know the Prime Meridian the name of the principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. in the latitude/longitude system passes through Greenwich, we will mark the location with a dot. At this point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , the circle can be bisected with a line passing through Greenwich. |  |
| Step 2. Fly around the globe along the 51st Parallel to create a 90° angle | |
|---|---|
| When you hop into your plane in Greenwich, England and begin to fly east, if you maintain that bearing, you will be flying along at 51.4° N, or approximately the 51st parallel. If you complete a 90° angle, you will land in Russia, just north of Mongolia . Mark this point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , and bisect the circle with a line passing through the point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. in Russia. Note the other half of the circle passes through a very remote part of Ontario, Canada. Label it 90° W between the North and South Poles on the left side of the circle, and 90°E on the Russian side. |  |
| Step 4. Add all of the angular measurements between 0° and 180°, then bisect the circle | |
|---|---|
| At this point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. , we need to mark all of the angular measurements between 0° and 180°, remembering we are still looking down at the North Pole from space. Bisect the circle at each of the remaining 178 locations (since we started with 0° and 180°, and marked 90° in step 2) | 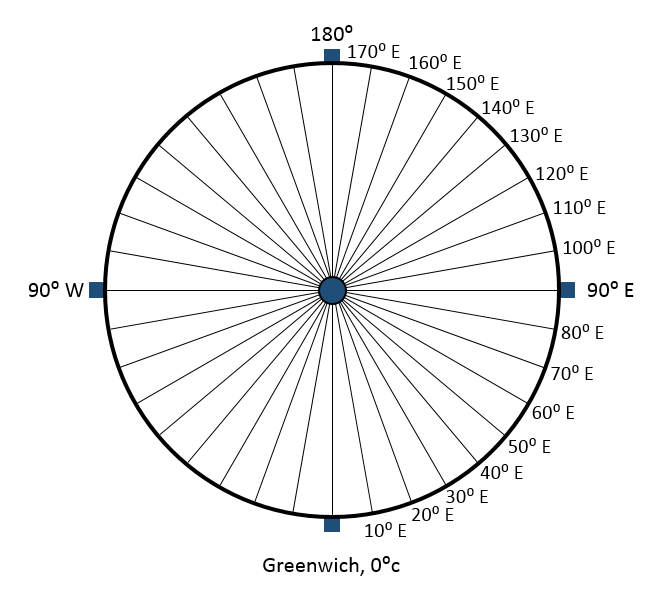 |
| Step 5. Add all of the labels using the idea of supplementary angles | |
|---|---|
| In geometry, supplementary angles add up to 180. Lines of longitude are supplementary angles in reference to Greenwich. If we are looking down on our labeled circle and we choose any point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. we've marked, then draw a straight line through the circle, we see the angle in the west to be supplementary to angle in the east. In this same fashion, lines of longitude are labeled with one measurement in the west (between the North and South poles) and the supplement of that angle in the east (also, between the North and South poles). |  |
Concept Quiz
2.4.4: Creating a Complete Geographic Grid
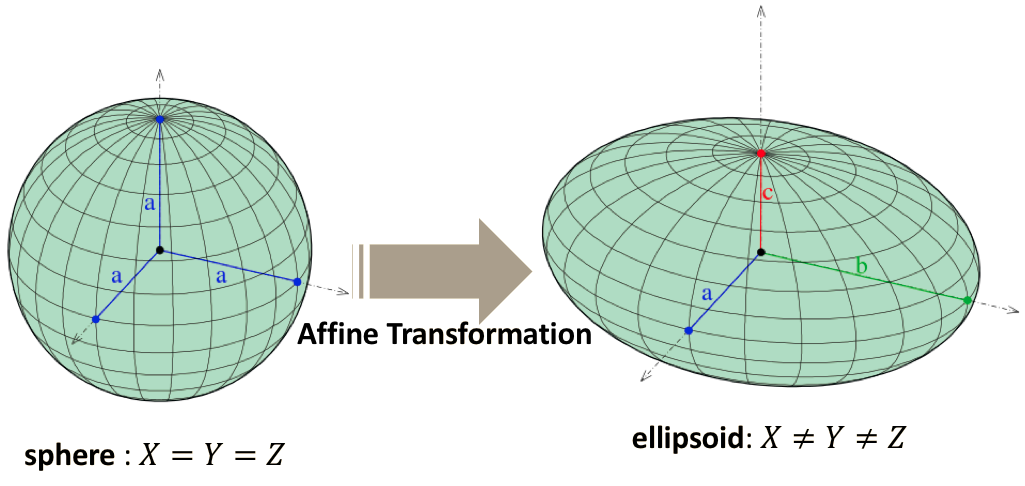 Now that we have looked at how the Earth-fixed, Earth-centered coordinate system is established for
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
and longitude, we need turn the sphere-based system in to an ellipsoid based system to complete the
geographic grid
the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a
principal meridian
the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian.
. We learned in Section Three that the Earth is best represented by an ellipsoid of revolution, more specifically, an
oblate spheroid
a sphere-like object which is wider than it is tall
and the
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
is best represented by an ellipsoid. In Section Four, we learned the definition of a
geodetic datum
the result of attaching a "free-floating"
reference ellipsoid
an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid
to a specifically measured
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
via control points and benchmarks.
is combining a
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
with a
reference ellipsoid
an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid
, connecting them via control points. In order to keep on-track with our definitions, we need to transform the sphere used to create the EFEC
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
/longitude coordinate system into not an
oblate spheroid
a sphere-like object which is wider than it is tall
, as we are not trying to represent the Earth, but instead into an ellipsoid to best-fit inside the
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
via a method called affine transformation. Affine transformation is a means of changing a sphere into an ellipsoid while maintaining straight lines.
Now that we have looked at how the Earth-fixed, Earth-centered coordinate system is established for
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
and longitude, we need turn the sphere-based system in to an ellipsoid based system to complete the
geographic grid
the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a
principal meridian
the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian.
. We learned in Section Three that the Earth is best represented by an ellipsoid of revolution, more specifically, an
oblate spheroid
a sphere-like object which is wider than it is tall
and the
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
is best represented by an ellipsoid. In Section Four, we learned the definition of a
geodetic datum
the result of attaching a "free-floating"
reference ellipsoid
an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid
to a specifically measured
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
via control points and benchmarks.
is combining a
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
with a
reference ellipsoid
an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid
, connecting them via control points. In order to keep on-track with our definitions, we need to transform the sphere used to create the EFEC
latitude
also known as 'parallels'
the east-west portion of a geographic grid measured with angles between 0 and 90°
/longitude coordinate system into not an
oblate spheroid
a sphere-like object which is wider than it is tall
, as we are not trying to represent the Earth, but instead into an ellipsoid to best-fit inside the
geoid
a model of the variation between global mean (average) sea level and
local mean sea level
the measurement above or below the global average at a single
point
A GIS
vector data
in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects
geometry type which is made up of just one
vertex
pl. vertices
One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature.
, marking a single XY location in any given geographic or projected coordinate system.
on the Earth's surface used for recording the elevation of
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
's
relief
the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features
, which is used to measure precise elevations on the
topographic surface
a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write."
via a method called affine transformation. Affine transformation is a means of changing a sphere into an ellipsoid while maintaining straight lines.
After we took all the time to carefully create the lines of latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude and we understand they are used to grid-out and label locations on the Earth's surface, we'd like to take that hard work and preserve it over in the reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid . All we are really doing is linearly stretching the measurement of the radius into a semi-minor and a different semi-major axis. By increasing the measurements of the radius, we are able to create an ellipsoid without curving the straight lines.
| The Main Point... |
|---|
| Our overall goal is to create a geographic coordinate system. To accomplish that, we need to first create a datum, which combines a geoid a model of the variation between global mean (average) sea level and local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features , which is used to measure precise elevations on the topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." and a reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid , since an ellipsoid is a better representation of a geoid a model of the variation between global mean (average) sea level and local mean sea level the measurement above or below the global average at a single point A GIS vector data in any sort of digital science or art, is simply denoting a type of graphical representation using straight lines to construct the outlines of objects geometry type which is made up of just one vertex pl. vertices One of a set of ordered x,y coordinate pairs that defines the shape of a line or polygon feature. , marking a single XY location in any given geographic or projected coordinate system. on the Earth's surface used for recording the elevation of topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." 's relief the difference between the highest and lowest point within a particular area while landforms are the descriptive words for individual features , which is used to measure precise elevations on the topographic surface a detailed map of the surface features of land. It includes the mountains, hills, creeks, and other bumps and lumps on a particular hunk of earth. The word is a Greek-rooted combo of topos meaning "place" and graphein "to write." . A reference ellipsoid an ellipsoid that is drawn to best-fit an area. World reference ellipsoids are drawn to best-fit the entire geoid; local ellipsoids are best fit on one side to a single place of the geoid is really just an plain old ellipsoid until a geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. has been applied to it, and that geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. starts out as an Earth-fixed, Earth-centered coordinate system, such as the latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° and longitude system. After the EFEC system is complete, it is necessary to use and affine transformation to "convert" the sphere into an ellipsoid. An affine transformation maintains the straight lines of the latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° /longitude system between the sphere and the ellipsoid. |
Concept Quiz
2.4.5: Additional Resources for Latitude and Longitude
YouTube Break: The Clock That Changed the World
An explanation of using time for navigation (the longitude problem) and satellite navigation ( trilateration the process of determining absolute or relative locations of points by measurement of distances, using the geometry of circles, spheres or triangles. ... In contrast to triangulation, it does not involve the measurement of angles ).
Run Time: 29 minute, but really well done and quite interesting. Highly recommended to better understand the geographic grid the result of using an established angular unit of measure to label the intersections of north-south and east-west lines on the surface of the Earth starting the labels at a principal meridian the north-south line from which the labeling begins. East-west lines have a very obvious start point: the equator. North-south lines must start somewhere, so when it is established for a particular geographic grid, it can be considered the principal meridian. that is longitude and latitude also known as 'parallels' the east-west portion of a geographic grid measured with angles between 0 and 90° .
- Note: SatNav = GPS Global Positioning System: A satellite-based navigation system owned and operated by the United States Department of Defense that provides location and time information anywhere on Earth. Receiver
Read All About It
Dork out on the math behind the concepts
(Everyone Read the Summary (pg. 6-7); the rest is optional if you're interested)